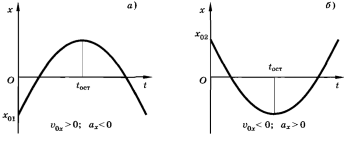
График зависимости координаты от времени

Второй билет

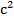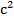Ускорение – величина, показывающая быстроту изменения скорости с течением времени. Единицы измерения ускорения: м/ ; км/ ; см/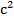

1 м/ 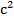это такое ускорение, при котором тело за 1 секунду изменяет свою скорость на 1м/с.

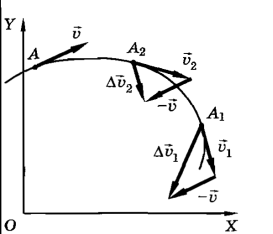Вектор среднего ускорения равен отношению изменения скорости ∆ 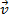к интервалу времени ∆t, за который произошло изменение скорости. Вектор 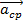имеет одинаковое направление с вектором ∆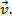

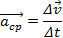
Нужно уметь определять ускорение в каждой точке траектории. Мгновенное ускорение – предел отношения изменения скорости ко времени, за которое это изменение произошло, если интервал времени ∆t стремится к нулю.

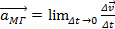
Мгновенное ускорение всегда направлено в сторону вогнутости траектории.

Равноускоренное прямолинейное движение – движение, при котором за любые равные промежутки времени вектор скорости изменяется одинаково.

Пусть в начальный момент времени 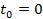скорость была 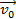. Тогда в произвольный момент времени скорость 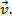То есть

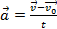
Отсюда

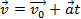
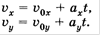
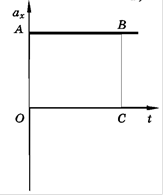В проекциях на оси

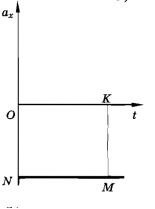
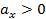
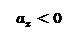разгон торможение

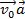
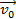
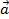
х х

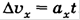По графику проекции ускорения можно найти, кроме 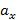, изменение проекции скорости. Оно численно равно площади прямоугольника ОАВС или OKMN, так как а 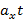численно равно площади прямоугольника ОАВС или OKMN. Площадь берется со знаком минус если .

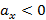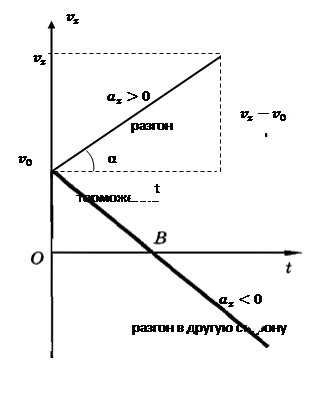График скорости

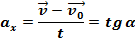
Представление перемещения по графику скорости

При равноускоренном движении, изменение координаты можно определить с помощью графика зависимости скорости от времени. Проекция скорости линейно изменяется.

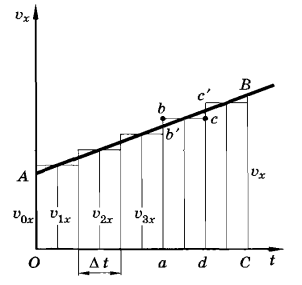
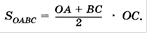Длина отрезка ОС численно равна времени t движения тела. Разделим его на nмалых одинаковых интервалов ∆t. Значения проекции скорости, соответствующих серединам этих промежутков времени, обозначим через 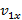, , 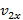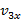и т.д. Построим на каждом из отрезков, численно равным промежуткам ∆t, прямоугольники, высоты которых численно равны проекциям скоростей 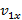, , 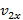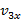и т.д. Площади этих прямоугольников численно равны изменениям координаты ∆ 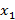, ∆ , ∆ 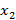, 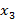… за промежутки времени ∆t, если считать, что движение в течение каждого такого промежутка является равномерным. Сумма площадей всех прямоугольников равна площади трапеции OABC. Чтобы это движение совпало с истинным, необходимо уменьшать промежутки времени ∆t, то ∆t 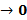. То площадь трапеции OABC станет равной изменению координаты ∆x за время t.

Длины ОА и ВС этой трапеции численно равны проекциям 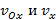, а ОС – времени движения t.

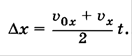
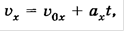Учитывая, что

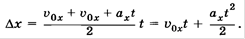Получим

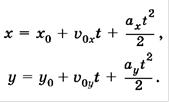Координаты при равноускоренном движении: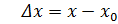

График зависимости координаты от времени.

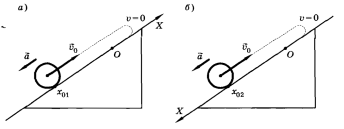
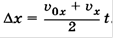Связь между проекциями начальной и конечной скоростей, ускорения и перемещения

Согласно формуле

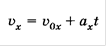Время t выразим из формулы

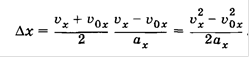
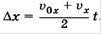
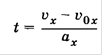
И подставив в по получим

Закон нечетных чисел

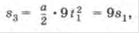
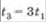
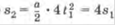
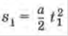Если за произвольный промежуток времени 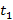от начала движения тело совершило перемещение , то за промежуток 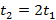( отсчитанный от того же момента) оно пройдет , за промежуток - перемещение .

При увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с 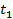, модули соответствующих векторов перемещений возрастают как ряд квадратных последовательных чисел.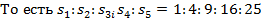

Модули векторов перемещений, совершаемых за последовательно равные 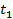промежутки времени, относятся как ряд последовательных нечетных чисел. То есть .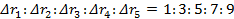