Расчет характеристик активного торможения

Время и путь активного торможения определяются по выражениям, вытекающим из формул:

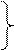Т _{актив. торм.} = t₁ + t₂

S _{актив. торм.} = S₁ + S₂ + S₃ [28]

здесь: t₁ - время первого периода активного торможения (периода реверса движителей) (с);

t₂ - время второго периода активного торможения (с);

S₁ - величина сноса судна течением (м);

S₂ - путь, проходимый судном за первый период торможения (м);

S₃ - путь, проходимый судном во второй период торможения (м).

В свою очередь вышеуказанные величины определяются по выражениям, вытекающим из формул [29;30;31;32]:

t₁ - принимается равным 25 с;

t₂ = G₁ E (υ₁ + c) / υ₀²_∞:

t_{2 0,0} = 0,836 × 608 (4,64 + 0) / 5,6 ² = 75 (с);

t_{2 0,2} = 0,843 × 608 (4,43 + 0) / 5,6 ² = 72 (с);

t_{2 0,4} = 0,849 × 608 (4,15 + 0) / 5,6 ² = 68 (с);

t_{2 0,6} = 0,856 × 608 (3,69 + 0) / 5,6 ² = 61 (с);

t_{2 0,8} = 0,862 × 608 (2,98 + 0) / 5,6 ² = 50 (с);

S₁ = С × T _{акт. торм.} [29]

S₂ = μ₂ υ_0∞ t₁ ( l - 3.63 t₁ / t_cв,тopм):

S_{2 0,0} = 1 × 5,6 × 25 (l - 3.63 × 25/1045) = 127.8 (м);

S_{2 0,2} = 0,962 × 5,6 × 25 (l - 3.63 × 25/999,9) = 122.4 (м);

S_{2 0,4} = 0,907 × 5,6 × 25 (l - 3.63 × 25/953,6) = 114.9 (м);

S_{2 0,6} = 0,817 × 5,6 × 25 (l - 3.63 × 25/902,2) = 102.8 (м);

S_{2 0,8} = 0,675 × 5,6 × 25 (l - 3.63 × 25/795,8) = 83.7 (м);

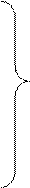S₃ = G₂E (υ₁² – c²) / υ₀²_∞:

S_{3 0,0} = 0,407 × 608 (4,64 ² – 0²) / 5,6² = 169.8 (м);

S_{3 0,2} = 0,411 × 608 (4,43 ² – 0²) / 5,6² = 156 (м); [30]

S_{3 0,4} = 0,415 × 608 (4,15 ² – 0²) / 5,6² = 138,5 (м);

S_{3 0,6} = 0,419 × 608 (3,69 ² – 0²) / 5,6² = 110,6 (м);

S_{3 0,8} = 0,423 × 608 (2,98² – 0²) / 5,6² = 72.6 (м);

В этих выражениях: μ₂, G_l , G₂ - вспомогательные функции глубины, определяемые по выражениям :

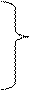для судов с открытыми винтами:

μ₂ = 1 - 0. 173 t_H- 0.365 (t_H)³

для судов всех типов: [31]

G₁ = 0.836 + 0.033 t_H

G2 = 0.407 + 0.020 t_H

Е - модуль инерционности (м);

υ_0∞ = 5,6 (м/с) – скорость полного переднего хода на глубокой воде;

t _{св. торм} – время свободного торможения судна на данной глубине, (с);

С = 1 (м/с) – скорость течения ( "+" для движения по течению, "-" для движения против течения);

υ₁ - скорость движения судна в конце первого периода активного торможения, определяемая по формуле :

υ₁ = μ₂ υ_0∞ / (1+ 8.54 t₁ / t _{св. торм}), (м/с); [32]

υ_{1 00} = 1 × 5,6 / (1+ 8.54 × 25/1045) = 4,6 (м/с);

υ_{1 0,2} = 0,962 × 5,6 / (1+ 8.54 × 25/999,9) = 4,43 (м/с);

υ_{1 0,4} = 0,907 × 5,6 / (1+ 8.54 × 25/953,6) = 4,15 (м/с);

υ_{1 0,6} = 0,817 × 5,6 / (1+ 8.54 × 25/902,2) = 3,69 (м/с);

υ_{1 0,8} = 0,675 × 5,6 / (1+ 8.54 × 25/795,8) = 2,98 (м/с);

После анализа расчетных таблиц и графиков зависимостей делаем вывод по инерционным характеристикам судна (состава).

Результаты расчета характеристик активного торможения представляются в таблице 2.7.

Таблица 2.7 – Расчет характеристик активного торможения

tH	—	0.0	0.2	0.4	0.6	0.8
Н	М	∞	9,5	4,8	3,1	2,4
μ2	—		0,962	0,907	0,817	0,675
G1	—	0,836	0,843	0,849	0,856	0,862
G2	—	0,407	0,411	0,415	0,419	0,423
t св. торм	С		999,9	953,6	902,2	795,8
S2	М	136,9	122,4	114,9	102,8	83,7
течение отсутствует, С = 0
t2	С
Т актив. торм.	С
S1	М
S3	М	169,8		138,5	110,6	72,6
S акт торм	М	297,6	278,4	253,4	213,4	156,3
движение по течению, С = + 1
t2	С	91,4	88,4	84,7	77,8	66,5
Т актив. торм.	С	116,4	113,7	109,7	102,8	91,5
S1	М	116,4	113,7	109,7	102,8	91,5
S3	М	161,9	148,4	130,5	102,5	64,2
S акт торм	М	406,1	384,5	355,1	308,1	239,4
движение против течения С = - 1
t2	С	58,9	56,0	51,8	44,6	33,1
Т актив. торм.	М	83,9	81,0	76,8	69,6	58,1
S1	М	-83,9	-81,0	-76,8	-69,6	-58,1
S3	С	161,9	148,4	130,5	102,5	64,2
S акт торм	М	205,84	189,8	168,6	135,7	89,8

По результатам расчета, приведенным в таблице 2.7, строятся графики зависимостей Т_{акт. торм} = f (H), S _{акт. торм} = f (H). Рисунки 5,6,7

Рис.5 – Зависимость параметров активного торможения от глубины при движении в стоячей воде

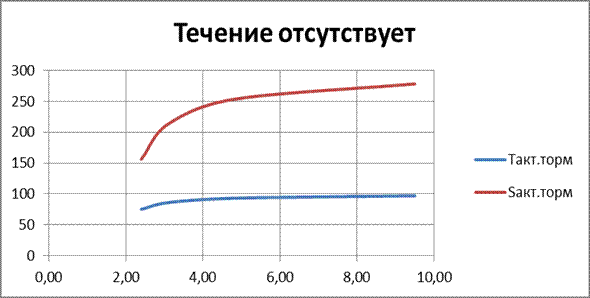
Рис.6 – Зависимость парметров активного торможения от глубины при движении по течению

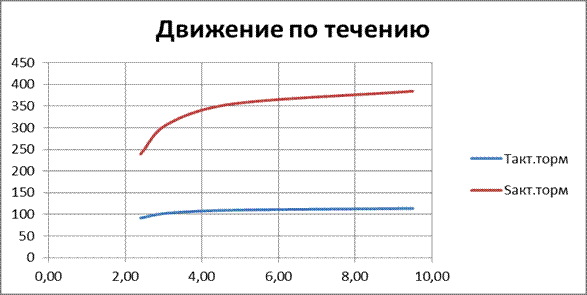
Рис.7 – Зависимость параметров активного торможения от глубины при движении против течения

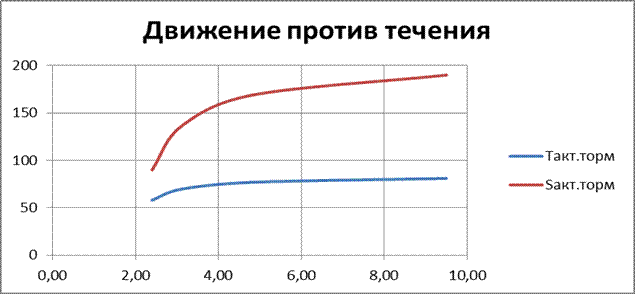
Вывод: Из графика пути и времени разгона (Рис. 4) судна видно, что при увеличении глубины эти параметры возрастают бесконечно приближаясь, но не достигая каких-то конкретных величин. Малая величина пути и времени разгона говорит о хороших скоростных и маневренных качествах судна.

Из графика пути и времени свободного торможения (Рис. 5) видно, что эти параметры увеличиваются при возрастании глубины судового хода. При больших глубинах они стремятся к каким-то определенным значениям, но никогда их не достигают. Иначе говоря, большой путь свободного торможения свидетельствует о хороших гидродинамических качествах судна.

Из графиков пути и времени активного торможения (Рис. 6) видно, что эти величины увеличиваются с возрастанием глубины, стремясь к каким-то определенным значением, но никогда их не достигая.

Также на все выше перечисленные величины влияет скорость течения: при ее увеличении также увеличиваются и все параметры (Т_раз ; S_раз ; Т _{св. торм.} ; S_{св. торм.}; Т_{акт. торм} ; S _{акт. торм}.)

При выполнении судном маневров судоводитель должен знать инерционные качества судна при данных условиях (глубине судового хода, скорости течения и т.д.).

СПЕЦИАЛЬНЫЕ ВОПРОСЫ УПРАВЛЕНИЯ СУДНОМ