Вращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.9).

Промежуток времени, в течение которого тело совершает один полный оборот вокруг оси, — период вращения. Величина, обратная периоду, — частота вращения.

Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.

Так как расстояния между точками твердого тела должны оста­ваться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.

φ=f(t).

Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорение ε.

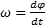или ω= .

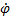числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак ω определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки, ω>0, а когда по ходу часовой стрелки, то ω<0.

Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что то же, 1/с (с^-1), так как радиан – величина безразмерная.

Угловую скорость тела можно изобразить в виде вектора 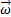, модуль которого равен | 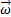| и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.10). Такой вектор определяет сразу и модуль угло­вой скорости, и ось вращения, и направ­ление вращения вокруг этой оси.

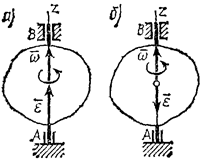
Рис.10

Угол поворота и угловая скорость характеризуют движение всего абсолютно твердого тела в целом. Линейная скорость какой-либо точки абсолютно твердого тела пропорциональна расстоянию точки от оси вращения:

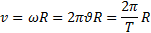
При равномерном вращении абсолютно твердого тела углы поворота тела за любые равные промежутки времени одинаковы, тангенциальные ускорения у различных точек тела отсутствуют, а нормальное ускорение точки тела зависит от ее расстояния до оси вращения:

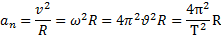
Вектор направлен к оси вращения.

Угловое ускорение характеризует изменение с те­чением времени угловой скорости тела. Если за промежуток вре­мени ∆t=t₁-t угловая скорость тела изменяется на величину ∆ω=ω₁-ω, то числовое значение среднего углового ускорения тела за этот промежуток времени будет 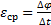. В пределе при ∆t→0 найдем,

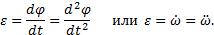
Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.

Размерность углового ускорения 1/T² (1/время²); в качестве единицы измерения обычно применяется рад/с² или, что то же, 1/с² (с-²).

Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины ω и ε имеют одинаковые знаки, и замедленным, - когда разные.

Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора ε, направленного вдоль оси вращения. При этом

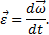
Направление ε совпадает с направлением ω, когда тело вращается ускоренно и (рис.10,а), противоположно ω при замедленном вращении (рис.10,б).