Физика звезд. 12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее

12.1 Энерговыделение происходит в объеме, и потому растет пропорционально кубу характерного размера объекта, теплоотвод же происходит с поверхности, а ее площадь возрастает как квадрат характерного размера. В итоге с увеличением размера тела (при сохранении темпа энерговыделения) его поверхностная температура должна расти. Дальше додумайте сами.

12.2 Молярная масса газа -- это среднее значение массы одной частицы газа, выраженное в атомных единицах массы. Своим низким значением молярная масса солнечного вещества обязана, во-первых, тому, что основной его компонентой (70% по массе) является водород, и, во-вторых, практически полной его ионизации. При ионизации атома водорода, масса которого почти равна атомной единице массы, появляются две частицы -- протон и электрон. Масса электрона пренебрежимо мала по сравнению с массой протона. Поэтому молярная масса чисто водородного полностью ионизованного газа близка к 0.5. В недрах Солнца молярная масса немного больше этого значения (0.6). Причина -- присутствие более тяжелых элементов (молярная масса чисто гелиевого полностью ионизованного газа равна 4/3 [поймите, почему], для чистого кислорода она близка к 2 и т. д.).

Полное число частиц, составляющих Солнце, можно оценить следующим образом:

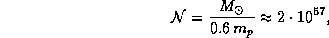
где 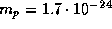г -- атомная единица массы. Вклад в массу наружных неионизованных слоев, где значение 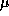больше, пренебрежимо мал.

12.3 При плотности в 150 г/см³ и средней молярной массе 0.6 (см. задачу ) концентрация частиц равна

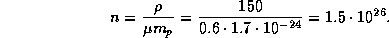
На самом деле средняя молярная масса в центре Солнца сейчас несколько больше, чем 0.6, так как водород там уже сильно выгорел, превратившись в гелий. Однако порядок величины n остается тем же, а только он нам и нужен.

Концентрация фотонов чернотельного излучения при температуре 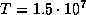равна (см. задачу )

Это на три с лишним порядка меньше концентрации частиц. Значит, и роль давления излучения в недрах Солнца мала (см. решение задачи ).

Любопытно, что, согласно расчетам моделей строения Солнца, в большей части его массы плотность 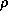и температура T связаны соотношением 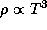. Поэтому отношение 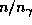, найденное нами для центра Солнца, характерно для его недр в целом. Фотонов в недрах Солнца (и всех звезд, кроме самых массивных) гораздо меньше, чем протонов.

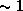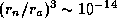12.4 Плотность воды 1 г/см³. При этом известно, что в жидкостях молекулы почти соприкасаются друг с другом. При плотностях, существенно больших плотности воды, имеющихся в недрах Солнца, атомы водорода ионизуются давлением. В результате доля объема, занятая частицами (соответственно атомами и голыми ядрами), уменьшается с до , где 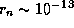см -- размер ядра, 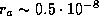см -- размер атома. Таким образом, ядра начнут соприкасаться и "мешать" друг другу лишь при плотностях 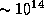г/см³. Это -- ядерные плотности. Они характерны для нейтронных звезд. В принципе вплоть до этих плотностей ионизованное вещество может оставаться газом.

Наряду с плотностью, агрегатное состояние звездного вещества определяется температурой. Так, известно, что при понижении температуры белого карлика атомные ядра в его недрах должны выстраиваться в кристаллическую решетку. Чтобы ядра атомов двигались свободно, т.е. образовывали газ, требуется, чтобы их кинетическая энергия kT существенно превосходила энергию кулоновского взаимодействия, равную по порядку величины 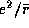, где 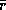-- среднее расстояние между ядрами. Условие 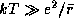с использованием соотношений (для чисто водородной плазмы)

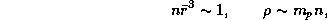
где n -- концентрация ядер, можно переписать в следующем виде:

или в числах

где 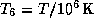. Для центра Солнца имеем 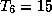, 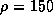г/см³ (см. предыдущую задачу), так что 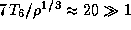. Итак, даже при плотности в 150 г/см³ вещество в центре Солнца из-за высокой температуры остается газом.

Дальнейшее придется принять на веру. Согласно расчетам моделей строения Солнца, соотношение 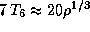, справедливое для центра Солнца, приближенно выполняется и в большей части его недр. Поэтому повсюду в недрах Солнца, а не только в его центре, вещество является газом.

12.5 Вычислим энергию, выделяющуюся при синтезе ядра атома гелия из четырех протонов. По формуле Эйнштейна 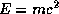имеем 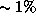, так как в ходе данной ядерной реакции (точнее, цепочки реакций синтеза 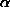-частицы из четырех протонов) "исчезает" 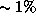(точнее, 0.7%) массы. Полная энергия покоя Солнца равна 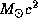. Если бы Солнце целиком состояло из водорода, то при полном его превращении в гелий выделилась бы энергия 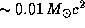. Время, на которое этой энергии хватило бы для поддержания светимости Солнца на ее нынешнем уровне, составляет 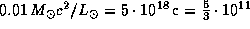лет. Коэффициент 5/3 "несерьезен" -- Солнце не целиком состоит из водорода и т. д. В действительности за время своей жизни на главной последовательности Солнце успеет сжечь лишь примерно 10% своих запасов водорода. Таким образом, Солнцу отпущено примерно 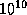лет "спокойной" жизни на главной последовательности, что вовсе неплохо!

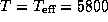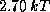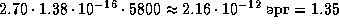12.6 Будем считать, что Солнце испускает чернотельное излучение с K. Средняя энергия, приходящаяся на один чернотельный фотон, равная (см. задачу ), составляет тогда эВ. Поэтому число фотонов, излучаемых Солнцем за счет энергии, выделяющейся при синтезе одной 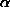-частицы, равно 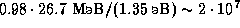шт. Так как при синтезе 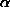-частицы из четырех протонов два из них за счет 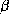-распада превращаются в нейтроны, то при этом рождаются два нейтрино. В итоге число ежесекундно излучаемых Солнцем фотонов оказывается в 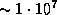раз больше числа испускаемых им нейтрино.

12.7 Вещество, аккрецируемое Солнцем, при падении достигает у его поверхности второй космической скорости 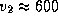км/с. Искомый темп аккреции 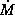определим из условия равенства кинетической энергии выпадающего за 1 с вещества и светимости Солнца:

откуда

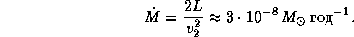
Как будет изменяться продолжительность года, т.е. период обращения Земли P при изменении массы Солнца? Из третьего закона Кеплера

находим

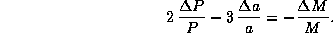
С другой стороны, должен сохраняться угловой момент 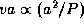, так что

Из этих двух соотношений находим, что

откуда при 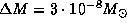получаем, что 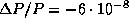. Это соответствует уменьшению продолжительности года на 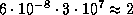c в год, чего явно не происходит. Можно поэтому с уверенностью утверждать, что Солнце светит не за счет аккреции.

12.8 По значениям температур можно заключить, что речь идет о массивных звездах, светимость которых обеспечивается CN-циклом. Известно, что темп энерговыделения при реакциях CN-цикла примерно пропорционален 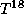. Поэтому искомое отношение равно 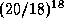. Не хватайтесь за калькулятор -- все можно подсчитать в уме, воспользовавшись замечательным пределом

Действительно,

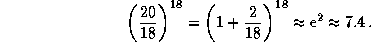
При росте температуры всего на 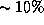темп энерговыделения возрастает более чем в 7 раз!

12.9 Ответ очевиден: один год. При меньшем периоде центробежная сила разорвет звезду.

12.10 Приравнивая центробежную силу на экваторе пульсара 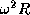к силе тяжести 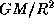, получаем предельную угловую скорость вращения: 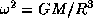. Быстрее вращаться пульсар не может, так как тогда центробежная сила разорвет его. Предельный период вращения есть 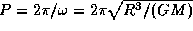. Плотность звезды с таким периодом вращения равна

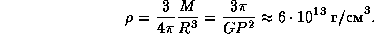
Это -- нижняя оценка плотности, при которой пульсар с периодом 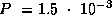с не будет еще разорван центробежной силой. Мы получили разумную оценку плотности нейтронных звезд. Она близка к ядерной: 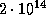г/см³.

12.11 Время схлопывания Солнца в точку -- это время свободного падения к центру Солнца тела, которое в начальный момент покоилось на его поверхности. Рассматривая движение такого тела, можно принять, что вся масса Солнца сосредоточена в центре (это допущение справедливо, если тело в процессе движения не обгоняет опадающие на центр слои, расположенные ниже; детальный анализ показывает, что это действительно так). Тогда время свободного падения равно половине периода P обращения тела по выродившейся в отрезок эллиптической орбите с большой полуосью 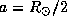(и эксцентриситетом e=1). Этот период мы вычислим по третьему закону Кеплера (см. также задачи и ):

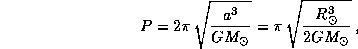
откуда для времени схлопывания Солнца 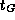(индекс G -- от gravitation) находим

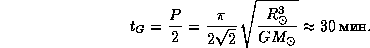
Это -- важное характерное время. При нарушениях механического равновесия заметные изменения должны происходить на временах 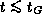. Поскольку никаких существенных изменений в состоянии Солнца не происходит на гораздо больших временных интервалах -- это прямой наблюдательный факт, -- то можно с уверенностью утверждать, что Солнце находится в механическом (гидростатическом) равновесии.

Использованные выше рассуждения дают следующее выражение для времени схлопывания произвольного сферически-симметричного самогравитирующего облака массы M, первоначально имевшего радиус R:

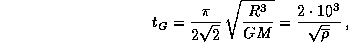
где 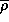-- начальная средняя плотность облака. Подставив сюда 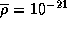г/см³, найдем, что время схлопывания межзвездного облака такой начальной плотности составля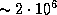ет лет.

12.12 Проведем анализ размерностей фигурирующих в задаче величин (ср. задачу ). У нас имеются следующие размерные параметры: масса "планеты" (или лучше сказать -- самогравитирующего тела) M, ее радиус R, размерная постоянная K, входящая в уравнение состояния 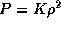и, наконец, постоянная тяготения G. Пусть [Q] -- размерность величины Q. Тогда, с одной стороны, , с другой же стороны ньютонова сила тяготения 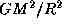, отнесенная к площади поверхности сферы радиуса R, также имеет размерность давления: 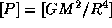. Отношение двух фигурирующих здесь комбинаций определяющих размерных величин есть отвлеченное число. Обозначим его 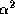, так что

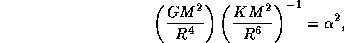
откуда

Следует ожидать, что 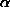-- число порядка единицы: так "всегда" бывает.

Из полученного сейчас выражения следует, что радиус самогравитирующей равновесной конфигурации, построенной из вещества с уравнением состояния 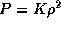, однозначно определяется значением K. Замечательно, что масса M выпала. Отсюда можно заключить, что от добавления массы или от удаления с тела части его вещества радиус "планеты" меняться не будет. Оказывается поэтому, что если вещество имеет уравнение состояния 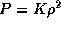, то в один и тот же объем можно поместить любую массу. В действительности, конечно, масса все же будет ограничена сверху, так как при добавлении вещества гравитационная потенциальная яма будет становиться глубже. Скорость убегания

будет расти 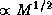. Когда она станет приближаться к скорости света c, должны начать проявляться отклонения поля тяготения от ньютонова за счет эффектов общей теории относительности.

Полученный результат -- независимость R от M -- кажется настолько невероятным, что сначала верится в него с трудом. Подтвердим его более детальным анализом (менее подготовленные читатели могут его пропустить). Это позволит получить значение 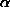. После этого поймем "на пальцах", в чем же суть дела, и обсудим некоторые важные для физики компактных звезд заключения общего характера, которые можно сделать на основе анализа нашей простой задачи.

Переходим к более аккуратному рассмотрению, которое позволит нам получить 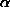. Уравнение механического равновесия самогравитирующей сферически-симметричной конфигурации (звезды, планеты) имет вид

При 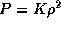это дает

Здесь 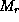-- масса в сфере радиуса r, так что

Поэтому из предыдущего уравнения следует, что

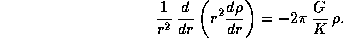
Если ввести

то это уравнение приводится к виду

где

Мы пришли к уравнению, по форме совпадающему с уравнением гармонических колебаний. (Для этого достаточно было догадаться ввести новую неизвестную y вместо 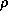.) Общее его решение имеет вид

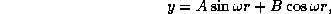
где A и B -- произвольные постоянные. При r=0 значение 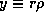равно, очевидно, нулю, и поэтому B=0. Итак,

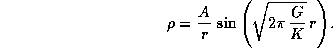
На поверхности тела, при r=R, мы должны иметь 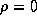, откуда находим

так что

Таким образом, аккуратный расчет полностью подтвердил то, что дал простой анализ размерностей. Безразмерный параметр 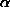действительно оказался близок к единице:

Если вдуматься, то неизменность радиуса при добавлении или удалении вещества не есть что-то невероятное. При добавлении массы, казалось бы, радиус будет возрастать. В этом "казалось бы" все и заключено. На самом деле добавляемое вещество имеет вес и потому сдавливает нижележащие слои. Если вещество несжимаемо, радиус тела растет 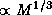. На этом простейшем случае и основана "интуиция" тех, кто не учитывает влияния сжимаемости на изменение радиуса при росте массы.

Если давление и плотность связаны степенной зависимостью

то говорят, что мы имеем дело с политропой индекса n. Рассматривавшийся нами случай соответствует n=1; при n=0 имеем несжимаемое вещество. Чем меньше n, тем труднее сжать вещество, тем оно "жестче". Теперь ясно, что при всех n<1 добавление массы сопровождается увеличением радиуса, в случае же n=1 нижние слои "проседают" под действием веса добавляемого вещества ровно на столько, что это компенсирует увеличение радиуса за счет добавления вещества. Если n>1, то с увеличением массы радиус должен убывать!

Бывает ли так? Да. Таковы, в частности, белые карлики. Чем больше масса белого карлика, тем меньше его радиус. При массах 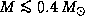эта зависимость имеет вид 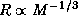(что соответствует политропе индекса n=3/2), при больших массах, а потому и больших плотностях, поскольку радиус убывает с M, скорость убывания радиуса увеличивается. Объяснение того, почему это происходит, завело бы нас слишком далеко. Ограничимся констатацией этого факта. При приближении массы к так называемому пределу Чандрасекара 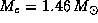достигаются столь большие плотности, что вещество начинает радикально менять свои свойства: электроны начинают захватываться ядрами, превращая имеющиеся в них протоны в нейтроны. Идет процесс нейтронизации вещества. Белых карликов с массой, большей чандрасекаровского предела, в природе нет и быть не может -- зато могут быть и есть такие нейтронные звезды.