Архитектура сетей Кохонена

Сети Кохонена (Kohonen T.) [3–4, 9] относятся к самоорганизующимся нейронным сетям. Самоорганизующаяся сеть позволяет выявлять кластеры (группы) входных векторов, обладающих некоторыми общими свойствами. При этом выделяют сети с неупорядоченными нейронами (часто называемые слоями Кохонена) и сети с упорядочением нейронов (часто называемые картами Кохонена). Карты Кохонена отражают структуру данных таким образом, что близким кластерам данных на карте соответствуют близко расположенные нейроны.

Сеть Кохонена — это однослойная сеть, каждый нейрон которой соединен со всеми компонентами ‑мерного входного вектора. Количество нейронов

В качестве нейронов сети Кохонена применяются линейные взвешенные сумматоры. Для обучения сети применяются механизмы конкуренции. Если обозначить вектор весов 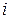‑го нейрона сети Кохонена как , то сеть работает следующим образом. При подаче на вход сети вектора побеждает тот нейрон, веса которого в наименьшей степени отличаются от соответствующих компонентов входного вектора. Для нейрона‑победителя выполняется соотношение

,

где 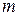— количество нейронов, — номер нейрона‑победителя, — расстояние (в смысле выбранной метрики) между векторами и .

Чаще всего в качестве меры расстояния используется эвклидова мера

.

Используются и другие меры расстояния (метрики) [2].

Веса нейрона-победителя подвергаются обучению (адаптации) по правилу Кохонена [1, 2]

где — коэффициент скорости обучения 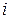‑го нейрона.

В пакете Neural Network Toolbox системы MATLAB принято следующее обозначение сети Кохонена (рис. 3.1). Сеть Кохонена — это слой конкурирующего типа (Competitive Layer), поскольку в нем применена конкурирующая функция активации. Здесь использован блок ndist для вычисления отрицательного евклидова расстояния между вектором входа p и строками матрицы весов IW11 (строка матрицы весов — это веса одного нейрона сети). Отрицательное евклидово расстояние вычисляется функцией negdist по формуле z = -sqrt(sum(w-p)^2)

Рис. 3.1. Архитектура слоя Кохонена

Вход функции активации n¹ — это результат суммирования отрицательного евклидова расстояния с вектором смещения b. Если все смещения нулевые, максимальное значение n¹ не может превышать 0. Нулевое значение n¹ возможно только, когда вектор входа p оказывается равным вектору веса одного из нейронов. Если смещения отличны от 0, то возможны и положительные значения для элементов вектора n¹.

Конкурирующая функция активации (блок C на рис. 3.1) анализирует значения элементов вектора n¹ и формирует выходы нейронов, равные 0 для всех нейронов, кроме одного "нейрона-победителя", имеющего на входе максимальное значение. Таким образом, вектор выхода имеет единственный элемент, равный 1, который соответствует нейрону-победителю, а остальные равны 0. Таким образом, в сети Кохонена используются нейроны типа WTA (Winner Takes All — победитель получает все). Номер активного нейрона определяет ту группу (кластер), к которой наиболее близок входной вектор.