Коэффициент увеличения момента

(1) Общий расчетный момент, включая момент с учетом эффектов второго порядка, рассчитывается путем увеличения изгибающих моментов, которые были определены с учетом эффектов первого порядка, а именно

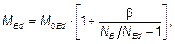(5.28)

где M_0Ed — момент с учетом эффектов первого порядка, см. также 5.8.8.2 (2);

b — коэффициент, который зависит от распределения моментов с учетом эффектов первого и второго порядка; см. 5.8.7.3 (2) и (3);

N_Ed — расчетное значение продольного усилия;

N_B — критическая сила, определенная на основе номинальной жесткости.

(2) Для отдельных элементов с постоянным поперечным сечением и продольным усилием момент с учетом эффекта второго порядка может быть принят исходя из синусоидального распределения. Тогда

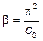, (5.29)

где с₀ — коэффициент, который зависит от распределения момента с учетом эффектов первого порядка (например, c₀ = 8 при постоянном моменте с учетом эффектов первого порядка, c₀ = 9,6 — при параболическом и c₀ = 12 — при симметричном треугольном распределении и т. д.).

(3) Для элементов конструкции без поперечной нагрузки отличающиеся друг от друга концевые изгибающие моменты с учетом эффектов первого порядка, М₀₁ и М₀₂, могут быть заменены эквивалентным постоянным моментом с учетом эффектов первого порядка, М_0е, согласно 5.8.8.2 (2). При принятии постоянного момента с учетом эффектов первого порядка, как правило, необходимо применять с₀ = 8.

Примечание — Значение с₀ = 8 действительно также для элементов с изгибом в двух направлениях. Следует указать на то, что в некоторых случаях, в зависимости от гибкости и продольного усилия, концевые моменты могут быть больше, чем увеличенный эквивалентный момент.

(4) В случае, когда условия 5.8.7.3 (2) или (3) не применимы, то b = 1 является целесообразным упрощением. Формула (5.28) может быть сокращена до следующего вида:

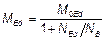. (5.30)

Примечание — Указания 5.8.7.3 (4) действительны также для общего расчета определенных типов кон­струкций, например для конструкций, которые подкреплены поперечными стенами, или более простых, когда главным эффектом воздействия являются изгибающие моменты в раскрепляющих элементах. Для других типов конструкций более широкий подход приведен в разделе Н.2 (приложение Н).

Метод, основанный на номинальной кривизне

Общие положения

(1) Данный метод применяется, прежде всего, для отдельно стоящих элементов с постоянной продольной силой и определенной расчетной длиной l₀ (см. 5.8.3.2). Метод определяет номинальный момент с учетом эффектов второго порядка, на основе перемещения, которое, в свою очередь, получено на основе расчетной длины и рассчитанной максимальной кривизны (см. также 5.8.5 (3)).

(2) Полученный расчетный момент применяется для расчета поперечных сечений при действии изгиба с продольной силой согласно 6.1.

Изгибающие моменты

(1) Расчетный момент

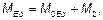(5.31)

где M_0Ed — момент с учетом эффектов первого порядка, включая влияние несовершенств,
см. также 5.8.8.2 (2);

М₂ — номинальный момент с учетом эффектов второго порядка, см. также 5.8.8.2 (3).

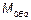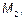Максимальное значение M_Ed рассчитывается из распределения и причем последнее может быть принято параболическим или синусоидальным вдоль расчетной длины.

Примечание — Для статически неопределимых элементов конструкции 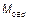определяется для фактических краевых условий, причем 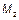зависит от краевых условий по расчетной длине; сравни с 5.8.8.1 (1).

(2) Для элементов без нагрузок, приложенных между концами элементов, различающие концевые изгибающие моменты с учетом эффектов первого порядка, M₀₁ и М₀₂, могут быть заменены эквивалентным моментом с учетом эффектов первого порядка, М_0е.

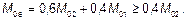(5.32)

M₀₁ и М₀₂ имеют те же знаки, если они вызывают растяжение на одной и той же стороне, в противном случае они имеют противоположные знаки. Кроме этого, |M₀₂| ³ |М₀₁|.

(3) Номинальный расчетный момент с учетом эффекта второго порядка, М₂, в формуле (5.31)
составляет:

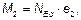(5.33)

где N_Ed — расчетное значение продольного усилия;

е₂ — перемещение, определяемое (1/r) · l₀²/c;

1/r — кривизна, см. 5.8.8.3;

l₀ — расчетная длина, см. 5.8.3.2;

с — коэффициент, который зависит от распределения кривизны, см. 5.8.8.2 (4).

(4) При постоянном поперечном сечении обычно используется с = 10 (≈p²). Если момент с учетом эффектов первого порядка является постоянным, то, как правило, необходимо проверять меньшее значение (8 — это нижнее предельное значение, которое соответствует постоянному общему моменту).

Примечание — Значение p² соответствует синусоидальному распределению кривизны. Значение для постоянной кривизны — 8. Необходимо обратить внимание на то, что с зависит от вида общей кривизны, в то время как с₀, согласно 5.8.7.3 (2), зависит от кривизны, соответствующей моменту с учетом эффектов первого порядка.

Кривизна

(1) Для элементов с постоянными симметричными сечениями (включая арматуру) применяется следующая формула:

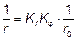, (5.34)

где K_r — корректирующий коэффициент, зависящий от продольной нагрузки, см. 5.8.8.3 (3);

К_j — коэффициент, учитывающий влияние ползучести, см. 5.8.8.3 (4);

,

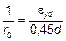здесь ;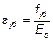

d — полезная высота, см. 5.8.8.3 (2).

(2) Если вся арматура не сконцентрирована у противоположных сторон, а частично распределена параллельно плоскости изгиба, то d определяется по формуле

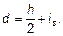(5.35)

При этом i_s — радиус инерции площади всей арматуры.

(3) K_r в формуле (5.34) следует принимать следующим образом:

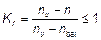, (5.36)

где 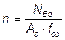— относительное продольное усилие;

здесь N_Ed — расчетное значение продольного усилия;

n_bal — значение n при максимальном сопротивлении изгибу; допускается принимать равным 0,4;

,

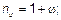
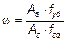где A_s — общая площадь сечения арматуры;

А_с — общая площадь сечения бетона.

(4) Влияние ползучести следует учитывать коэффициентом

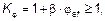(5.37)

где j_ef — эффективный коэффициент ползучести, см. 5.8.4;

;

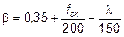l — гибкость, см. 5.8.3.1.

Двухосный изгиб

(1) Общий метод, описанный в 5.8.6, может быть также использован для двухосного изгиба. Следующие правила действительны, когда применяются упрощенные методы. Особое внимание необходимо уделить нахождению сечения элемента с критической комбинацией моментов.

(2) В качестве первого шага необходимо произвести раздельный расчет в направлениях обеих главных осей, без учета двухосного изгиба. Несовершенства необходимо учитывать только в направлении, в котором они больше всего приводят к самым неблагоприятным воздействиям.

(3) Не требуется никакой дальнейшей проверки, если для гибкости выполняются следующие условия:

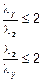и (5.38а)

и если относительный эксцентриситет e_y/h и e_z/b (рисунок 5.8), удовлетворяет одному из условий:

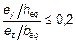или 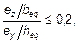(5.38b)

где b, h — ширина и высота сечения;

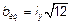и

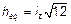— для эквивалентного прямоугольного сечения,

здесь i_y, i_z — радиусы инерции соответственно относительно оси y и оси z;

l_у, l_z — гибкость l₀/i соответственно относительно оси y и оси z;

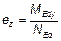— эксцентриситет нагрузки в направлении оси z;

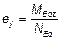— эксцентриситет нагрузки в направлении оси у,

здесь M_Edy — расчетное значение момента относительно оси y, включая моменты с учетом эффекта второго порядка;

M_Edz — расчетное значение момента относительно оси z, включая моменты с учетом эффекта второго порядка;

N_Ed — расчетное значение продольного усилия для соответствующего сочетания нагрузок.

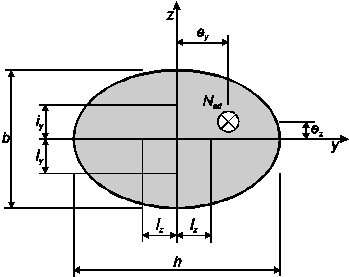
Рисунок 5.8 — Определение эксцентриситетовe_y и e_z

(4) Если не выполняются условия (5.38), то необходимо учитывать двухосный изгиб, включая влияние эффектов второго порядка в обоих направлениях (если ими нельзя пренебречь согласно 5.8.2 (6) или 5.8.3). При отсутствии более точного расчета сечений при двухосном изгибе может быть использован следующий упрощенный критерий:

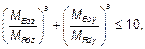(5.39)

где M_Edz/y — расчетный момент относительно соответствующей оси, включая момент от эффектов второго порядка;

M_Rdz/y — предельный момент в соответствующем направлении;

a — показатель степени:

для круглых и эллиптических сечений а = 2;

для прямоугольных сечений:	NEd/NRd	0,1	0,7	1,0
a	1,0	1,5	2,0

для промежуточных значений допускается линейная интерполяция,

здесь N_Ed — расчетное значение продольной силы;

N_Rd = A_cf_cd + A_sf_yd — расчетное значение сопротивления сечения продольной силе,

A_c — площадь брутто бетонного сечения;

A_s — площадь продольной арматуры.