Построение эпюры материалов и определение мест обрыва продольных стержней

Вцеляхэкономиисталичастьпродольнойарматуры(до50%максимальнойрасчетнойплощади)можетнедоводитьсядоопорыиобрыватьсявпролете,гдеонанетребуетсяпорасчету.Местатеоретическогообрыва стержнейопределяютсяс помощью эпюры материалов.

Точноезначениеместтеоретическогообрывастержнейопределяютаналитически,используяуравнение(3.4).Решениеегоотносительно x = lдает

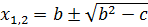, (3.12)

где 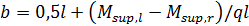; ; 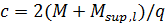в зависимости от загружения q = g или q = g + p; M – изгибающий момент, воспринимаемый в сечении необорванными стержнями.

Определим точки теоретического обрыва крайнего ригеля.

Для пролетной арматуры: l = 5,0 м; загружение №1 (индекс 310), q = g + p= 94,73 кН/м; 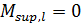; ; 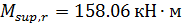M = 144 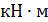; b =

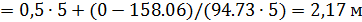; c = ; ; ; .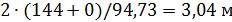

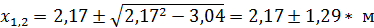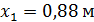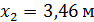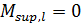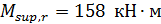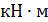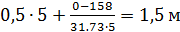Для арматуры на опоре B (1-я группа): загружение №3 (индекс 330), q = g + p = 31.73 кН/м; ; ; M = -122.6 ; b = ; c = ; ; .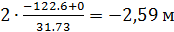

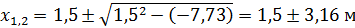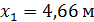Для арматуры на опоре B (2-я группа): M = 0; b = 1,5 м; c =0; ; .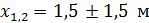

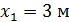Для пролетной арматуры: l = 5,0 м; загружение №1 (индекс 310), q = g + p = 94,73 кН/м; 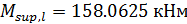; ; 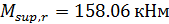M = 81 ;

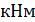b 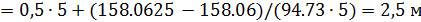; c = ; ; ; .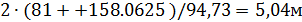

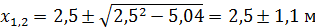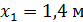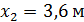Дляобеспеченияпрочностинаклонныхсеченийригеляпоизгибающиммоментамобрываемыевпролетестержнипродольнойарматурынеобходимозавестизаточкутеоретическогообрыванарасстояние не менее 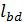, определяется по формуле:

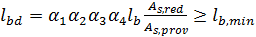. (3.13)

Для пролетной арматуры крайнего ригеля обрываются стержни 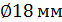класса S500. Требуемая площадь сечения арматуры 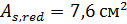( 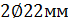), принятая площадь сечения арматуры 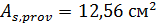( 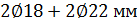). По таблице Ж.2 базовая длина анкеровки 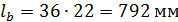. Длина анкеровки обрываемых стержней в соответствии с формулой (3.13): .

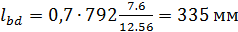Минимальная длина анкеровки:

- ;

- ;

- .

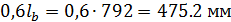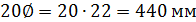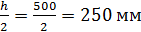Окончательно принимаем .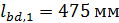

Для арматуры опоры B крайнего ригеля обрываются стержни 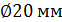класса S500. Требуемая площадь сечения арматуры 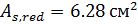( 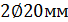), принятая площадь сечения арматуры 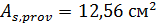( 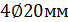). По таблице Ж.2 базовая длина анкеровки ; .

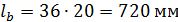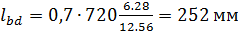Минимальная длина анкеровки:

- ;

- ;

- .

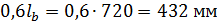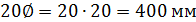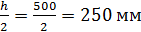Окончательно принимаем .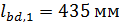

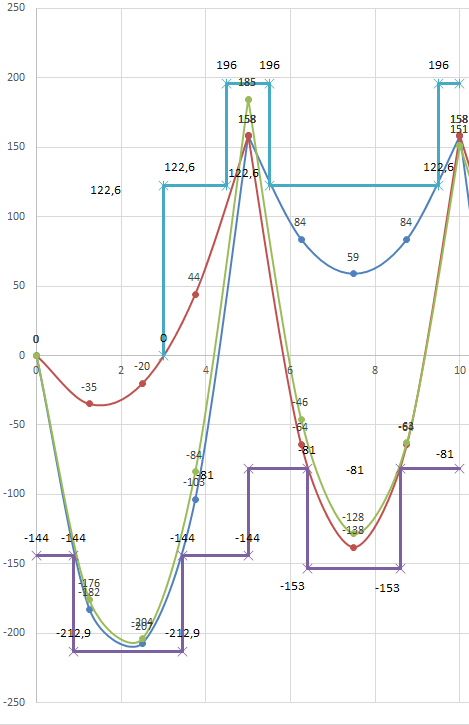
Рисунок 3.4 – Эпюры материалов

Расчет по раскрытию трещин,нормальных к продольной оси ригеля

Определимширину раскрытиятрещинригеляпервогопролетапризагружении№1,котороевызываетнаибольшийизгибающиймомент. Момент от нормативных длительных действующих нагрузок

.

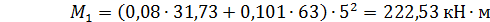Геометрические характеристики сечения:

;

;

;

;

;

.

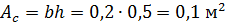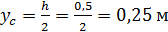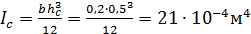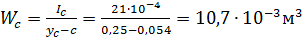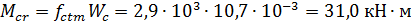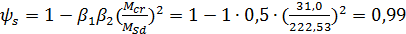Процент армирования сечения ,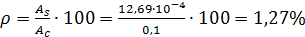

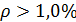, следовательно,z = 0,8d;

;

;

.

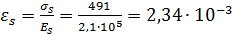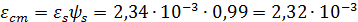Эффективный коэффициент армирования равен:

;

;

.

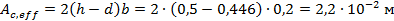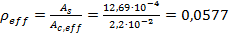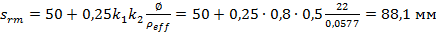Расчетная ширина раскрытия трещин равна:

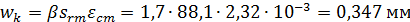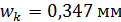; . Ширина раскрытия трещин меньше допустимой: .

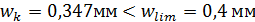Расчет прогиба ригеля

Проверкужесткости ригеляследуетпроизводитьиз условия 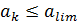, где –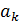

прогибригеля от действиявнешнейнагрузки; 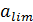– предельно допустимый прогиб (приложение Е).

Определимпрогибригеляпервогопролетапризагружении№1.Изпредыдущегорасчета 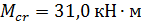, 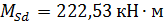. Геометрические характеристики сечения:

Эффективный модуль упругости

;

;

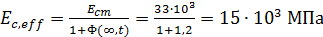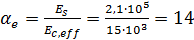Высота сжатой зоны

;

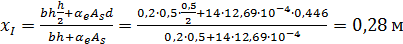Момент инерции сечения без трещин в растянутой зоне

;

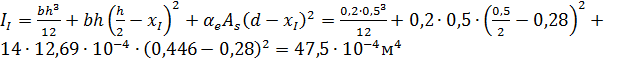Момент инерции сечения с трещинами

;

.

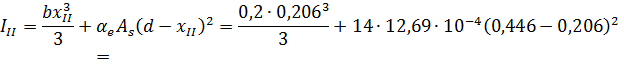
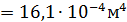Изгибная жесткость

.

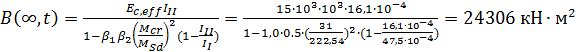Коэффициент 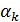определяем по 9-й строке таблицы Ж.1.

; ;

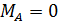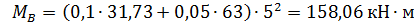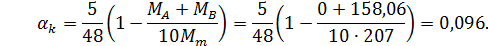
Величина прогиба

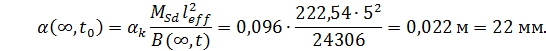
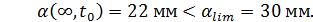
Жесткость ригеля обеспечена.