Расчет давления льда на единичную опору при термическом расширении
Литература
- Пехович А.И. Основы гидроледотермики. Л.: Энергоатомиздат, 1983, 200 с.
Общие пояснения
При изменении температуры воздуха ледяной покров может оказывать давление на инженерные сооружения из-за термического расширения льда. Процесс возрастания давления происходит достаточно медленно, поэтому ледовое давление рассматривается как статическое. Статическое давление возникает в ледяном покрове при его тепловом расширении только в том случае, когда сооружение препятствует его свободному расширению. Величина ледового давления зависит от характера изменения во времени температуры воздуха.
Мерой тепловой деформации льда являются коэффициентов линейного a объемного g расширения льда, которые задаются следующими формулами:
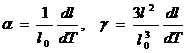 (7.1)
(7.1)
где 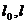 первоначальный и после воздействия температуры линейные размеры льда соответственно. С физической точки зрения формулы (7.1) показывают, как изменяется относительная длина или относительный объем при изменении температуры на 10. Из этих формул следует, что
первоначальный и после воздействия температуры линейные размеры льда соответственно. С физической точки зрения формулы (7.1) показывают, как изменяется относительная длина или относительный объем при изменении температуры на 10. Из этих формул следует, что 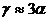 .
.
Аномальные свойства морского льда проявляются в процессе термического расширения. При термическом расширении в морском льду протекают два различных физических процесса: собственно термическое расширение отдельных компонентов льда и изменение их относительной массы при фазовых переходах. В зависимости от температуры и солености льда будет превалировать тот или иной процесс. Например, при понижении температуры входящие в состав морского льда пресный лед и соли сжимаются, но общий объем единицы массы морского льда возрастает. Это происходит потому, что вымерзает часть рассола и образуется дополнительная масса льда. Коэффициент объемного расширения морского льда 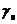 можно рассчитать по формуле:
можно рассчитать по формуле:
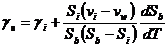 , (7.2)
, (7.2)
где 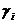 - коэффициент объемного расширения пресноводного льда;
- коэффициент объемного расширения пресноводного льда; 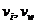 - удельные объемы льда и воды соответственно;
- удельные объемы льда и воды соответственно; 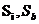 - соленость льда и рассола. В этой формуле не учитываются изменения объема, связанные с переходом солей в твердое состояние или в рассол. Коэффициент объемного расширения льда приведен в таблице 7.1, его связь с коэффициентом линейного расширения задается следующим выражением:
- соленость льда и рассола. В этой формуле не учитываются изменения объема, связанные с переходом солей в твердое состояние или в рассол. Коэффициент объемного расширения льда приведен в таблице 7.1, его связь с коэффициентом линейного расширения задается следующим выражением: 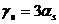 .
.
Таблица 7.1
Коэффициент объемного расширения морского льда, 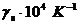
| Т, 0С | Соленость морского льда, 0/00 | ||||||||
| -2 | 1.6 | -22.7 | -46.9 | -71.2 | -95.5 | -119.7 | -180.3 | -241.0 | -301.6 |
| -4 | 1.6 | -4.5 | -10.5 | -16.6 | -22.6 | -28.7 | -43.8 | -58.9 | -74.0 |
| -6 | 1.5 | -1.1 | -3.8 | -6.4 | -9.1 | -11.8 | -18.4 | -25.1 | -31.8 |
| -8 | 1.5 | 1.4 | -0.8 | -2.0 | -3.1 | -4.3 | -7.3 | -10.2 | -13.1 |
| -10 | 1.5 | 0.7 | -0.1 | -0.9 | -1.7 | -2.5 | -4.6 | -6.7 | -8.7 |
| -12 | 1.5 | 1.0 | 0.4 | -0.3 | -0.9 | -1.5 | -1.0 | -4.5 | -6.0 |
| -14 | 1.5 | 1.1 | 0.6 | 0.2 | -0.3 | -0.8 | -1.9 | -3.1 | -4.2 |
| -16 | 1.5 | 1.2 | 0.8 | 0.5 | 0.1 | -0.3 | -1.2 | -2.1 | -3.0 |
| -18 | 1.5 | 1.3 | 1.0 | 0.7 | 0.4 | 0.1 | -0.7 | -1.4 | -2.1 |
| -20 | 1.4 | 1.3 | 1.1 | 0.8 | 0.6 | 0.3 | -0.2 | -0.9 | -1.5 |
| -22 | 1.4 | 1.4 | 1.2 | 1.0 | 0.8 | 0.5 | 0.0 | -0.5 | -1.0 |
| -24 | 1.4 | 1.0 | 0.4 | -0.2 | -0.8 | -1.4 | -2.9 | -4.4 | -5.9 |
| -26 | 1.4 | 1.2 | 1.0 | 0.6 | 0.3 | 0.0 | -0.7 | -1.5 | -2.3 |
| -28 | 1.4 | 1.4 | 1.2 | 1.0 | 0.8 | 0.6 | 0.2 | -0.3 | -0.8 |
| -30 | 1.4 | 1.4 | 1.3 | 1.2 | 1.1 | 0.9 | 0.6 | 0.3 | 0.0 |
Как следует из табл. 7.1 коэффициент объемного расширения морского льда существенным образом зависит от температуры льда и его солености. Расчет давления морского льда на сооружение может быть выполнен только численно, поэтому в расчетной работе методика будет изложена применительно к пресному льду.
Расчетные формулы для ледового давления
При расчетах воздействия пресного льда при термическом расширении принимается, что ледяной покров жестко защемлен в плане и имеет возможность расширяться только в вертикальном направлении. Для описания процесса используется математическая модель вязкого течения льда, которая описывается уравнениями Навье-Стокса и неразрывности:
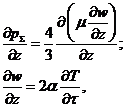 (7.3)
(7.3)
где 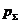 - напряжения в ледяном покрове;
- напряжения в ледяном покрове; 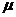 - коэффициент динамической вязкости льда;
- коэффициент динамической вязкости льда; 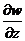 - скорость деформации льда;
- скорость деформации льда; 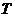 - температура льда;
- температура льда; 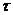 - время;
- время; 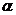 - коэффициент линейного теплового расширения льда.
- коэффициент линейного теплового расширения льда.
В предположении, что 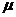 и
и 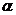 в данный момент времени постоянны по толщине льда
в данный момент времени постоянны по толщине льда 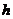 , решение уравнений (7.3) может быть записано следующим образом:
, решение уравнений (7.3) может быть записано следующим образом:
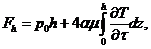 (7.4)
(7.4)
где 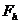 -погонная нагрузка в вертикальной плоскости ото льда на сооружение, Н/м;
-погонная нагрузка в вертикальной плоскости ото льда на сооружение, Н/м; 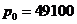 Н/м2 – напряжение, соответствующее предельной упругой деформациильда.
Н/м2 – напряжение, соответствующее предельной упругой деформациильда.
На поверхности ледяного покрова имеется переходное термическое сопротивление от воздуха к поверхности льда. Это сопротивление может быть учтено за счет увеличения толщины льда до значения 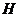 :
:
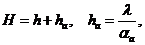 (7.5)
(7.5)
где 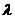 - коэффициент теплопроводности льда;
- коэффициент теплопроводности льда; 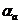 - коэффициент теплоотдачи на границе «лед – воздух».
- коэффициент теплоотдачи на границе «лед – воздух».
Формула (7.4) может быть переписана тогда в следующем виде:
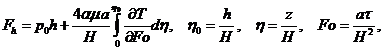 (7.6)
(7.6)
где 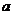 - коэффициент температуропроводности льда;
- коэффициент температуропроводности льда; 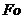 - число Фурье.
- число Фурье.
Окончательно в безразмерном виде выражение для давления льда на инженерное сооружение может быть записано следующим образом:
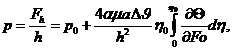 (7.7)
(7.7)
где 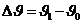 - разность между конечной и начальной температурами воздуха;
- разность между конечной и начальной температурами воздуха; 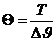 - безразмерный параметр температуры.
- безразмерный параметр температуры.
Определение давления при различных законах изменения температуры воздуха
Распределение температуры по толщине льда, входящее в выражение (7.7) находится из решения уравнения теплопроводности:
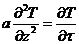 (7.8)
(7.8)
При следующих граничных условиях для линейного закона:
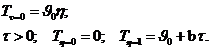 (7.9)
(7.9)
Решение краевой задачи (7.8) – (7.9) может быть получено в замкнутом виде с помощью бесконечных рядов, использование которых при выполнении расчетов весьма затруднительно. Для выполнения расчетов давление льда на сооружение представляется в следующем виде:
Для линейного закона:
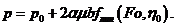 (7.10)
(7.10)
Значения функции 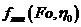 определяется по графикам, приведенным на рис. 7.1.
определяется по графикам, приведенным на рис. 7.1.
Выбор расчетного значения вязкости льда
Вязкость льда рассчитывается по следующим формулам в зависимости от температуры льда, она определяется в Па∙с:
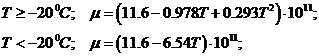 (7.11)
(7.11)
исходя из средней температуры деятельного слоя 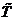 :
:
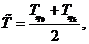 (7.12)
(7.12)
где 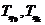 - температуры верхней и нижней границы деятельного слоя.
- температуры верхней и нижней границы деятельного слоя.
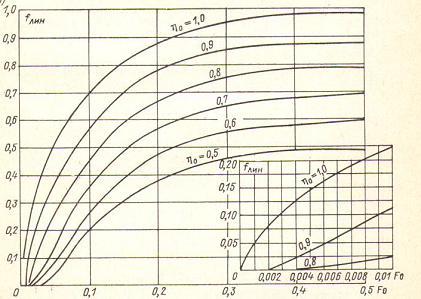
Рис. 7.1 Значения функции 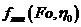
Под деятельным слоем обычно понимают слой льда, который реагирует на изменение температуры. Для этого слоя приближенно выполняется следующее равенство:
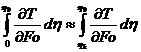 (7.13)
(7.13)
Толщина деятельного слоя изменяется в течение времени. Она зависит также от характера изменения температуры воздуха и условий теплообмена на поверхности льда. Верхней границей деятельного слоя является поверхность ледяного покрова. Нижняя граница определяется по графику, представленному на рис. 7.2.
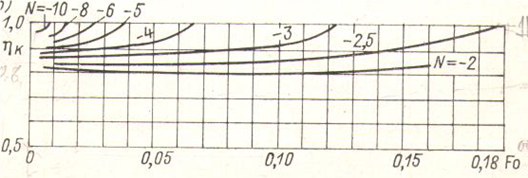
Рис. 7.2 График для определения нижней границы деятельного слоя.
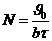
Для выполнения расчетов по формуле (7.12) необходимо знать температуру на границах деятельного слоя. Даже на верхней границе деятельного слоя, которая совпадает с поверхностью ледяного покрова температура не будет равно температуре воздуха из-за наличия термического сопротивления (см. формулу (7.5)). Определение этих температур выполняется по следующим формулам:
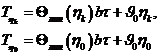 , (7.14)
, (7.14)
где параметр температуры 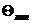 определяется с помощью графика, представленного на рис. 7.3.
определяется с помощью графика, представленного на рис. 7.3.
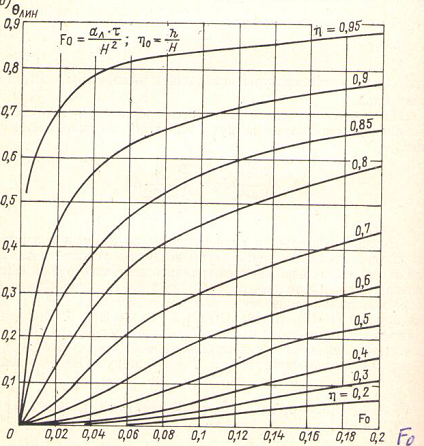
Рис.7.3 Зависимость 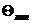 от параметров.
от параметров.
Исходные данные
Исходные данные для выполнения работы представлены в табл. 7.2, варианты 0 ¸ 9.
Таблица 7.2
| Характеристика | Номер варианта | |||||||||
| Толщина льда , м | 0,8 | 0,85 | 0,9 | 0,95 | 1.1 | 1.05 | 0.97 | 0.88 | 0.75 | |
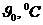 | -15 | -17 | -20 | -22 | -25 | -23 | -21 | -19 | -16 | -12 |
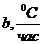 | 0,5 | 0,8 | 0,9 | 1,2 | 1,3 | 0,75 | 0,65 | 0,6 | 0,7 | |
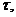 часы часы | ||||||||||
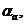 Вт/(м2∙К) Вт/(м2∙К) | ||||||||||
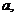 м2/с м2/с | 1.13∙10-6 | |||||||||
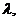 Вт/(м∙К) Вт/(м∙К) | 2.2 | |||||||||
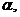 К-1 К-1 | 5.5∙10-5 |
Примечание: При выполнении расчетов обращайте внимание на размерность физических величин.
Порядок выполнения работы
1. Рассчитать ледовое давление на сооружение.Привести подробные результаты расчетов
a. Рассчитать величины 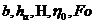 .
.
b. Определить 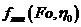 .
.
c. Определить 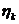 .
.
d. Определить температуру границ деятельного слоя.
e. Определить среднюю температуру деятельного слоя и рассчитать динамическую вязкость льда.
f. Рассчитать давление льда при термическом расширении.
Составление отчета
В отчет по лабораторной работе входят результаты расчетов и их анализ.
Требования к выполнению работ
Опыт преподавания показывает, что часто при выполнении расчетных работ студенты допускают различные нарушения давно установленных правил. В первую очередь это касается представления результатов расчетов и их графического оформления. Поэтому ниже приводятся основные правила выполнения расчетов и построения графиков, которые должны обязательно выполняться при выполнении расчетных работ (Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.М.: Наука, 1965, 608 с.).
Правила приближенных вычислений
При выполнении любых расчетов всегда необходимо помнить от точности получаемых результатов. Нельзя проводить вычисления с большим количеством цифр, чем количество верных значимых цифр в исходных данных.
Разница между точным числом х и его приближенным значениема называется погрешностью. Если справедливо неравенство 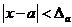 , то величина
, то величина 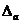 называется предельной абсолютной погрешностью приближенного числа
называется предельной абсолютной погрешностью приближенного числа 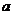 . Если абсолютная погрешность величины
. Если абсолютная погрешность величины 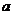 не превышает одной единицы разряда последней цифры числа
не превышает одной единицы разряда последней цифры числа 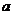 , то у него все знаки верные или все цифры значащие.
, то у него все знаки верные или все цифры значащие.
Обычно при выполнении массовых расчетов не проводят учет погрешности каждого отдельного результата. В таких расчетах применяется приводимые ниже правила подсчета цифр, которые позволяют считать, что в среднем полученные результаты будут иметь все знаки верные.
1. При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.
2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр.
3. При возведении в степень следует сохранять столько значащих цифр, сколько имеет возводимое в степень число.
4. Во всех промежуточных результатах следует сохранять одной цифрой более, чес рекомендовано выше. В окончательном результате эта цифра отбрасывается.
5. Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значимых цифр (умножение, деление, возведение в степень), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
Правила округления. Ели приближенное число содержит лишние знаки, то его необходимо округлить. При округлении сохраняются только значащие цифры, причем, если первая отбрасываемая цифра больше 4, то последняя сохраняемая увеличивается на 1. Если отбрасываемая часть состоит только из одной цифры 5, то округление осуществляется так, чтобы последняя цифра оставалась четной.
При выполнении расчетных заданий следует считать, что все указанные в исходных данных цифру значимые.
Правила построения графиков
1. Оформление осей, масштаб, размерность. Результаты измерений и вычислений удобно представлять в графическом виде. Графики строятся вручную на миллиметровой бумаге или с помощью соответствующих программ на компьютере; размеры графика не должны быть меньше 150*150 мм. На график прежде всего наносятся координатные оси. На концах осей наносятся обозначения физических величин и их единицы измерения. Затем на оси наносятся масштабные деления так, чтобы расстояние между делениями составляли 1, 2, 5 единиц (или 0.1, 0.2, 0.5, или 10, 20, 50 и т.д.). Обычно порядок масштаба, т.е. 10±n выносится на конец оси. Точка пересечения осей не обязательно должна соответствовать нулю по одной или более осям. Начало отсчета по осям и масштаб следует выбирать так, чтобы: а) кривая (прямая) заняла все поле графика; б) углы между касательными к кривой и осями должны быть близки к 45º ( или 135º) по возможности в большей части графика.
2. Графическое представление физических величин. После выбора и нанесения на оси масштабов на график наносятся значения физических величин. Их обозначают маленькими кружочками, треугольниками, квадратами и другими маркерами, причем числовые значения, соответствующие нанесенным точкам, не сносятся на оси. Затем от каждой точки вверх и вниз, вправо и влево откладываются в виде отрезков соответствующие погрешности в масштабе графика.
После нанесения точек строиться график, т.е. проводится плавная кривая или прямая так, чтобы она пересекала все области погрешностей или, если это не возможно, суммы отклонений экспериментальных точек снизу и сверху кривой должны быть близки. Построение графика можно осуществлять вручную или с помощью соответствующей программы на компьютере. Под графиком указывается название той зависимости, которая изображается графиком.
Рекомендованная литература
Алексеев Ю.Н., Астафьев В.Н., Литонов О.Е., Мансуров М.Р., Панов В.В., Трусков П.А. Ледотехнические аспекты освоения морских месторождений нефти и газа. СПб.:Гидрометеоиздат, 2001, 360 с.
Доронин Ю.П., Кубышкин Н.В. Рост и таяние морского льда СПб.:Гидрометеоиздат, 2001, 42 с.
Ионов Б.П., Грамузов Е.М. Ледовая ходкость судов. СПб: Судостроение, 2001, 512 с.
Лосет С., Шхинек К, Гудместад О., Хойланд К. Воздействие льда на морские и береговые сооружения. СПб., М., Краснодар: Лань, 2010, 272 с.
Морской лед. Сбор и анализ данных наблюдений, физические свойства и прогнозирование ледовых условий. Под ред. И.Е. Фролова и В.П.Гаврило. СПб, Гидрометеоиздат, 1997, 402 с.
Пехович А.И. Основы гидроледотермики. Л.: Энергоатомиздат, 1983, 200 с.
Сазонов К.Е. Теоретические основы плавания судов во льдах. СПб.:ЦНИИ им. акад. А.Н.Крылова, 2010, 274 с.
Цой Л.Г. Морские ледоколы. Особенности проектирования. Учебное пособие. СПбГМТУ, СПб., 2003, 110 с.
