Билет № 8: Алгоритм перевода целых чисел методом деления.

Метод поэтапного деления на основание с.с.заключается в последовательном выполнении действий:

1. Исходное число делим на основание с.с. с остатком в десятичной с.с.

2. Если часное от деления не равно 0, выпоняем п.1.

3. Полученные остатки записываем последовательно от последнего к первому.

4. Полученная запись - искомое двоичное число.

Например: переведем число 105 в двоичную с.с. методом поэтапного деления на основание с.с.

105₁₀ = 1101001₂

Методом поэтапного деления можно перевести целое десятичное число в любую позиционную систему счисления.

Билет №9 Алгоритм перевода правильной дроби методом деления. Пример

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.712

.712 • 2 = 1.424

.424 • 2 = 0.848

.848 • 2 = 1.696

.696 • 2 = 1.392

.392 • 2 = 0.784

и т. д.

Получим: 206,11610=11001110,00011101102

Билет № 10: Алгоритм перевода чисел методом «взвешивания».

Билет № 11: Алгоритм перевода чисел из 2-чн методом «замены».

1. Для того чтобы перевести число из двоичной системы в восьмерич­ную, необходимо выполнить следующие действия. Двигаясь от запятой влево и вправо, разбить двоичное число на группы по три разряда, допол­няя при необходимости нулями крайние левую и правую группы. Затем триаду заменить соответствующей восьмеричной цифрой.

Пример. Перевести число 10011001111,0101 из двоичной системы в восьмеричную.

Решение:

Триады					,
Восьмеричные цифры					,

Ответ: 2317,24₈.

2.Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим трёхразрядным двоичным числом (триадой), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.

Пример. Перевести число 204,4 из восьмеричной системы в двоичную.

Решение.

Восьмеричные цифры				,
Триады				,

Ответ: 10000100,1₂.

3. Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру этого числа соответствующим четырёхразрядным двоичным числом (тетрадой), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.

Пример. Перевести число 6СЗ,А из шестнадцатеричной системы в двоичную.

Решение:

Шестнадцатеричные цифры		C		,	A
Тетрады				,

Ответ: 11011000011,101₂.

Билет № 12: Формы представления чисел в ЭВМ.

Естественная форма

В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.

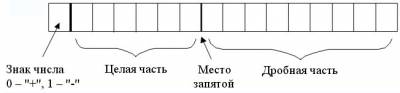
Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.

A = [A] · K^А,

где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, K^А - масштабный коэффициент.

Естественная форма числа в неявном, условном виде реализуется формулой:

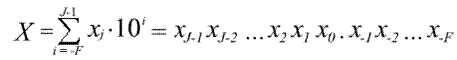
т.е. число записывается только с помощью набора значащих цифр x_j без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

С плавающей запятой (ПЛЗ) числа изображаются в виде:

X = ± M×P ^±r,

где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×10², 0,36×10^-2, –0,1082×10³.

Нормализованная экспоненциальная запись числа - это запись вида a= m*P^q, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом m - мантиссa числа, q - порядк числа.

Tо есть нормальная форма реализуется формулой: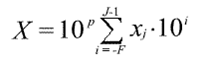

Нормальная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

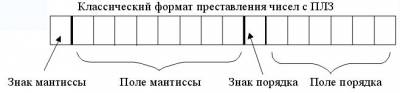
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, используется так называемый смещённый порядок, который рассчитывается по формуле 2^(a-1) + ИП, где a - количество разрядов, отводимых под порядок, ИП - истинный порядок.

В конкретной ЭВМ диапазон представления чисел с плавающей запятой зависит от основания системы и числа разрядов для представления порядка. При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Точность вычислений при использовании формата с плавающей запятой определяется числом разрядов мантиссы. Она увеличивается с увеличением числа разрядов.

Алгоритм представления числа с плавающей запятой:

1. перевести число из p-ичной системы счисления в двоичную;

2. представить двоичное число в нормализованной экспоненциальной форме;

3. рассчитать смещённый порядок числа;

4. разместить знак, порядок и мантиссу в соответствующие разряды сетки.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена информацией, экономии памяти и удобства операций над десятичными числами предусматриваются специальные форматы их представления: зонный (распакованный) и упакованный. Зонный формат используется в операциях ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.