Расчёт стержневых статически неопределимых систем на кинематическое воздействие

В плоской стержневой системе, степень статической неопределимости которой равна n, имеет место n независимых друг от друга кинематических возмущений, например, смещений линейных и угловых опорных связей (рис. 17.8,а). Жесткостные характеристики поперечных сечений элементов системы любого k-го участка на изгиб EJ_k, сдвиг GA_k и растяжение–сжатие EA_k примем постоянными.

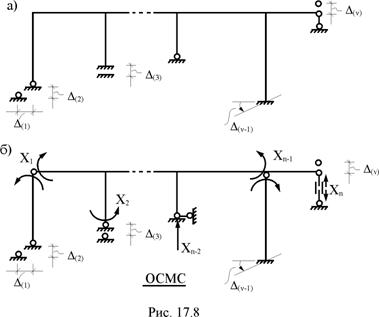
Удаляя из заданного сооружения n лишних связей (рис. 17.8,б), образуем статически определимую основную систему метода сил (ОСМС). Особое внимание при выборе основной системы следует обращать на удаление связей, получивших в рассчитываемом сооружении перемещение. В частности, при наличии кинематического возмущения линейной связи её отбрасывание недопустимо, так как в этом случае из расчётной схемы основной системы исключается связь с диском "земля", являющимся причиной рассматриваемого линейного смещения по направлению опорной связи. В этом случае в произвольное сечение смещаемой опорной связи вводится поступательный шарнир (рис. 17.8,б – правая вертикальная опора).

Неизвестные метода сил X₁, X₂, …, X_j, …, X_n определим из условий равенства нулю перемещений по направлениям X_i (i = 1, 2, …, n) в основной системе метода сил от неизвестных этого метода и заданного смещения связей. Повторяя выкладки, приведённые в п. 16.2 шестнадцатой лекции, получим систему канонических уравнений для определения неизвестных метода сил в случае кинематического воздействия на сооружение. Строка i этой системы уравнений имеет вид:

d_i1X₁ + d_i2X₂ + … + d_iiX_i + … + d_ijX_j + … + d_inX_n + D_ic = 0. (17.12)

Главные d_ii и побочные d_ij коэффициенты системы канонических уравнений определяются по формулам (16.5)–(16.6) в общем случае плоских стержневых систем и формулам (16.8)–(16.9) для рам и балок (см. п. 16.2 шестнадцатой лекции).

Свободный член j-й строки системы канонических уравнений D_ic есть перемещение по направлению усилия X_i в i-й удалённой лишней связи в основной системе метода сил от заданного кинематического возмущения. В статически определимой основной системе, принятой для расчёта, указанное перемещение определяется по формуле (12.6), полученной в п. 12.3 второй части настоящего курса лекций:

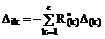. (17.13)

В формуле (17.13) 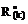– реакция в k-й связи, получившей кинематическое воздействие, от X_i = 1 в статически определимой основной системе; D_(k) – величина кинематического воздействия, например, смещения k-й опорной связи.

Как и при температурном воздействии, значения жесткостных характеристик поперечных сечений элементов сооружения EJ_k, GA_k, EA_k не входят в соотношение (17.13). Это значит, что численные значения усилий в лишних связях и, следовательно, внутренних усилий в заданном сооружении, есть функции абсолютных значений жесткостей поперечных сечений стержней.

Вычислив из системы канонических уравнений усилия в лишних связях, мы расчёт статически неопределимого сооружения на кинематическое воздействие (рис. 17.8,а) свели к расчёту статически определимой основной системы метода сил (рис. 17.8,б). Так как кинематическое воздействие в статически определимых сооружениях внутренних усилий не вызывает (см. п. 12.1 второй части настоящего курса лекций), то величины изгибающих моментов М_с, поперечных Q_c и продольных сил N_c в сечениях заданного сооружения в этом случае определяются только усилиями в лишних связях X₁, X₂, …, X_j, …, X_n. Имея эпюры внутренних усилий M_j, Q_j, N_j от Х_j = 1 в основной системе и применяя принцип независимости действия сил, получим:

M_с = M₁X₁ + M₂X₂ + … + M_jX_j + … + M_nX_n,

Q_с = Q₁X₁ + Q₂X₂ + … + Q_jX_j + … + Q_nX_n, (17.14)

N_с = N₁X₁ + N₂X₂ + … + N_jX_j + … + N_nX_n.

Эпюры внутренних усилий M_с, Q_с, N_с в заданном сооружении должны удовлетворять кинематическим условиям, а именно: перемещения по направлению любых усилий X­_i­ (i = 1, 2, …, n) в отброшенных связях в основной системе метода сил от действия всех упомянутых усилий X₁, X₂, …, X_j, …, X_n и от заданного кинематического возмущения должны быть равны нулю. Другими словами, численные значения перемещений по направлению X_i в статически определимой основной системе от всех неизвестных метода сил будут равны величинам перемещений, вызываемых кинематическим воздействием, с обратным знаком, т.е.

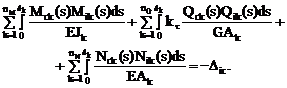(17.15)

Соотношение (17.15) по смыслу аналогично формуле (17.4), полученной в п. 17.1 для случая температурного воздействия на сооружение.

В матричной форме система канонических уравнений метода сил при кинематическом воздействии запишется:

dХ + D_с = 0. (17.16)

d – матрица внешней податливости принятой для расчёта заданного сооружения основной системы метода сил. Для вычисления её элементов используется матричное соотношение (16.21), полученное в п. 16.7 шестнадцатой лекции.

Х и D_с – соответственно, матрицы неизвестных метода сил и перемещений по направлению этих неизвестных от заданного кинематического воздействия в основной системе. Число строк в матрицах Х и D_с равно степени статической неопределимости сооружения, а число столбцов – числу вариантов кинематических возмущений.

В матричной форме соотношение (17.13) для вычисления элементов матрицы D_с запишется:

D_с = 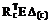. (17.17)

R_c – матрица реакций в связях, получивших кинематическое возмущение, от X₁ = 1, X₂ = 1, …, X_j = 1, …, X_n = 1 в статически определимой основной системе метода сил.

R_c = [R_c1 R_c2 … R_cj … R_cn].

D_(с) – матрица величин заданных кинематических возмущений по вариантам воздействий.

D_(с) = .

Число строк в матрицах R_c и D_(с) равно e – суммарному числу кинематических возмущений во всех вариантах воздействий; число столбцов: в матрице R_c – степени статической неопределимости сооружения n, в матрице D_(с) – числу вариантов кинематических воздействий n.

Е – единичная матрица порядка e´e, элементы которой учитывают знак "минус" формулы (17.13), т.е. отрицательны.

Е = diag [-1 -1 … -1 -1].

Матрицу неизвестных метода сил получим из системы канонических уравнений (17.16):

Х = –d^-1D_с. (17.18)

В развёрнутой форме соотношение (17.18) с учётом матричных выражений (16.21) и (17.17) перепишется:

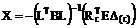. (17.19)

Напоминаем, порядок формирования матиц L и В изложен в п. 16.7 шестнадцатой лекции.

Внутренние усилия M_c, Q_c, N_c в заданном статически неопределимом сооружении от кинематического воздействия в матричной форме определим, используя соотношения (17.14).

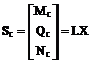. (17.20)

Матричное выражение (17.20) с учётом соотношения (17.19) в окончательной форме примет вид:

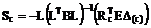. (17.21)

Кинематическая проверка правильности вычисления элементов матрицы S_c производится с помощью следующей матричной формулы:

L^T B S­_c = –D_c. (17.22)

Пример расчёта статически неопределимой рамы на смещение опорных связей в обычной форме

В раме, показанной на рис. 17.9,а, горизонтальная связь левой опоры получила перемещение влево на D₍₁₎ = 2 см, вертикальная связь этой же опоры – вниз на D₍₂₎ = 1 см. Изгибная жёсткость поперечных сечений стержней рамы известна и равна постоянной величине EJ. Требуется построить эпюры внутренних усилий от заданного смещения опорных связей.

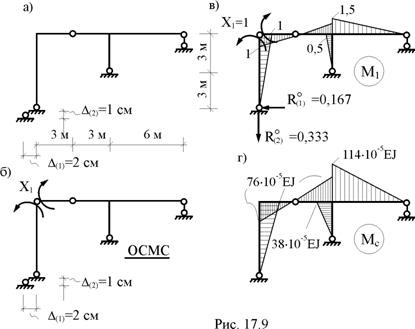
В п. 17.2 эта же рама была рассчитана на температурное воздействие. Некоторыми результатами этого расчета воспользуемся в рассматриваемом примере.

1. Определение степени статической неопределимости и выбор статически определимой основной системы метода сил (см. п. 17.2, рис. 17.9,б).

2. Построение эпюры изгибающих моментов М₁ и вычисление реакций в смещаемых связях 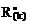в основной системе от Х₁ = 1 (рис. 17.9,в).

3. Вычисление коэффициентов разрешающего уравнения метода сил

d₁₁ Х₁ + D_1с = 0.

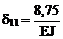(см. п. 17.2).

Перемещение по направлению Х₁ от заданного смещения опорных связей определим по формуле (17.13).

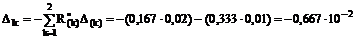(рад).

4. Решение уравнения метода сил:

.

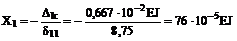5. Определение изгибающих моментов в характерных сечениях рамы от заданных смещений горизонтальной и вертикальной связей левой опоры и построение эпюры М_с (рис. 17.9,г). Из первого выражения группы соотношений (17.14) следует:

M_c = M₁X₁, где X₁ = 76 × 10^-5EJ.

6. Кинематическая проверка эпюры М_с по формуле (17.15). В этой формуле сохраним только первый член, учитывающий изгибные деформации элементов рамы.

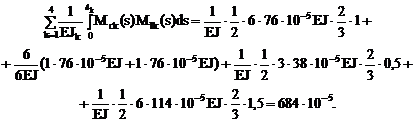
Результат сопряжения эпюр М_с и М₁ совпадает с численным значением правой части разрешающего уравнения метода сил d₁₁Х₁ = –D_1с = –(-0,667×10^-2) = 667×10^-5 с относительной погрешностью вычислений:

e = 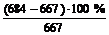= 2,55 %,

что подтверждает правильность вычисления ординат эпюры М_с.

7. Построение эпюры поперечных сил Q_c по эпюре изгибающих моментов М_с и эпюры продольных сил N_c по эпюре Q_c. Читателям предлагается самостоятельно выполнить построение эпюр Q_c и N_c.

Пример расчёта статически неопределимой рамы на смещение опорных связей в матричной форме

В раме, показанной на рис. 17.10, возможны следующие независимые друг от друга кинематические воздействия: первое – перемещение вертикальной связи левой опоры вниз на D₍₁₎ = 2 см, второе – перемещение горизонтальной связи вправо на D₍₂₎ = 1,5 см и вертикальной вверх на D₍₃₎ = 1 см опоры центральной стойки, третье – перемещение правой опоры вверх на D₍₄₎ = 3 см. Численные значения изгибных жесткостей поперечных сечений ригеля EJ_p и стоек EJ_с рамы заданы: EJ_p = 2 EJ, EJ_с = 0,5 EJ (EJ – известное число). Требуется вычислить элементы матрицы изгибающих моментов М_с для характерных сечений заданной рамы от каждого из вышеперечисленных кинематических воздействий.

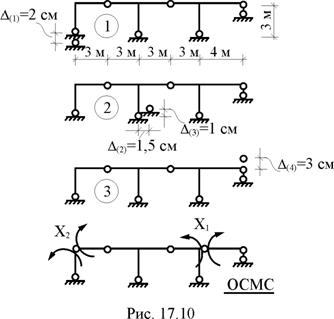
Для расчёта рамы в матричной форме с учётом только изгибных деформаций её элементов используем соотношение (17.21). В этом случае L = М, В = В_М, S_c = M_c и матричное выражение (17.21) примет вид:

.

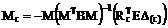В дальнейшем воспользуемся некоторыми результатами расчёта этой же рамы на силовое воздействие (см. п. 16.8 шестнадцатой лекции).

1. Выбор основной системы метода сил (рис. 16.14,б, рис. 17.10), построение в ней эпюр изгибающих моментов от Х₁ = 1, Х₂ = 1 (рис. 16.14,в,г), нумерация участков и сечений (рис. 16.16), формирование матриц изгибающих моментов в основной системе от Х₁ = 1, Х₂ = 1 и внутренней упругой податливости рамы М и В_М, вычисление элементов матрицы внешней податливости d = М^Т В_М М, обращение этой матрицы.

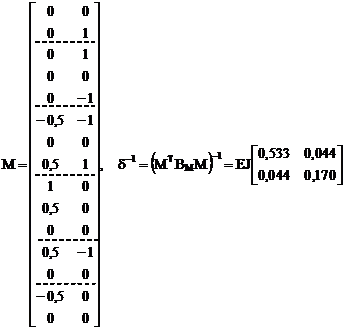
Примечание. Для расчёта рамы на температурное воздействие (см. п. 17.3) и в настоящем примере количество сечений на грузовых участках ригеля сохранено таким же, как и при расчёте рамы на силовое воздействие (рис. 16.16). Это обусловлено тем, что расчёт статически неопределимых систем на температурные и кинематические воздействия с помощью вычислительной техники производится вместе с расчётом на силовое воздействие. В частности, на кафедре строительной механике НГАСУ для расчёта статически неопределимых систем методом сил на все виды независимых друг от друга воздействий (силовые, температурные и кинематические) используется программа "Mefor", разработанная профессором В.Г. Себешевым.

2. Формирование матрицы реакций в связях, получивших перемещение, от Х₁ = 1, Х₂ = 1 в основной системе (рис. 17.11).

.

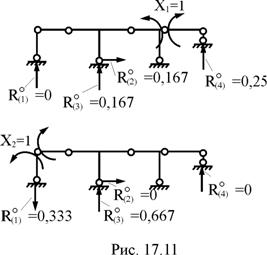
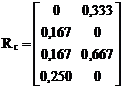В первой строке этой матрицы сначала от Х₁ = 1 (первый столбец), затем от Х₂ = 1 (второй столбец), зафиксированы реакции вертикальной связи левой опоры, во второй – реакции горизонтальной связи опоры центральной стойки, в третьей – вертикальной связи опоры центральной стойки, в четвёртой – правой опорной связи. Напоминаем, что реакция в смещаемой связи вносится в матрицу R_c со знаком "плюс", если её направление совпадает с направлением смещения связи, и со знаком "минус", – если не совпадает.

3. Составление матрицы величин перемещений опорных связей (в м) по вариантам воздействий.

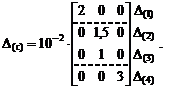
4. Вычисление матрицы перемещений по направлениям Х₁ и Х₂ от заданных кинематических возмущений в основной системе, или матрицы свободных членов системы канонических уравнений (17.16).

D_с = =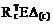

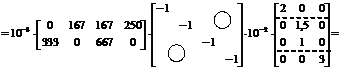
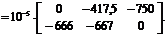
5. Определение элементов матрицы неизвестных метода сил.

X = –d^-1D_c = –(M^T B_M M)^-1 (R_c E D­_(c)) =

=

.

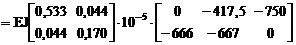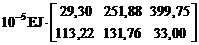6. Получение матрицы изгибающих моментов М_с в заданной раме по вариантам кинематических воздействий (рис. 17.10) в соответствии с принятой нумерацией участков и сечений (рис. 16.16).

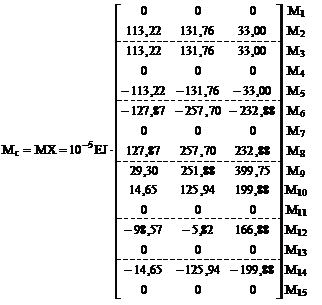
Читателям предлагается (используя соотношение (17.22), самостоятельно произвести кинематическую проверку правильности вычисления элементов матрицы М_с и построить для заданной рамы сначала эпюры изгибающих моментов, а затем и эпюры поперечных и продольных сил от упомянутых выше смещений опорных связей.

Вопросы для самопроверки

1. Задана статически неопределимая система (балка, рама, ферма или комбинированная система). Требуется произвести её расчёт на конкретное температурное или кинематическое воздействие. Определите степень статической неопределимости системы, выберите один из вариантов статически определимой основной системы и запишите в общем виде систему канонических уравнений метода сил для расчёта сооружения на заданное воздействие. Какой смысл имеет i-я строка системы канонических уравнений? Поясните смысл коэффициентов D_it и D_ic этой системы уравнений. Запишите формулы для определения этих коэффициентов. Что означают параметры M_ik(s), a_k, h_k, 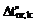, N_ik(s), , , 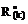D_(k), входящие в эти формулы?

2. Как определяются внутренние усилия в заданном статически неопределимом сооружении от температурных или кинематических воздействий, если известны усилия в лишних связях X₁, X₂, …, X_j, …, X_n?

3. Как производится проверка правильности эпюр внутренних усилий, полученных для заданного сооружения от температурных или кинематических воздействий?

4. Почему усилия в лишних связях X₁, X₂, …, X_j, …, X_n и ординаты эпюр внутренних усилий в статически неопределимом сооружении при его расчёте на температурные или кинематические воздействия зависят от абсолютного значения жесткостей поперечных сечений элементов сооружения?

5. Задано статически неопределимое сооружение, подверженное f независимым друг от друга температурным воздействиям или n, также независимым друг от друга, кинематическим воздействиям. Запишите в общем виде в матричной форме систему канонических уравнений метода сил для расчёта этого сооружения на температурные или кинематические воздействия. Сколько строк и столбцов содержится в матрицах D_t и D_с записанной системы уравнений?

6. Запишите матричные соотношения, используемые при расчёте статически неопределимых сооружений в случае температурных или кинематических воздействий:

а) для получения элементов матриц свободных членов D_t и D_с системы канонических уравнений метода сил;

б) для получения элементов матрицы неизвестных метода сил Х;

в) для определения элементов матриц внутренних усилий S_t или S_с для характерных сечений заданного сооружения.

7. Какую структуру имеют матрицы L_t, B_t, T, входящие в перечисленные в 6 вопросе матричные соотношения? Сколько строк и столбцов имеют матрицы L_t, B_t, T?

8. Поясните смыл элементов подматриц 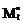, , 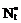B_t,nr, B_t,0, T_nr, T₀, а также матриц R_c, E, D_(c).

9. Сколько строк и столбцов имеют матрицы R_c, E, D_(c), если суммарное число смещаемых связей во всех n комбинациях кинематических воздействий равно e?

10. Сформулируйте правила знаков, используемых при формировании матриц L_t, T, R_c.

11. Как вычисляются элементы подматриц B_t,nr и B_t,0 матрицы температурной податливости сооружения B_t?

12. Каким образом в матричной форме производится кинематическая проверка правильности расчёта статически неопределимого сооружения на температурное или кинематическое воздействие? Запишите соответствующее матричное соотношение.

13. Поясните смысл следующих матричных выражений, используемых для расчёта статически неопределимых систем на температурное или кинематическое воздействие:

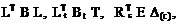
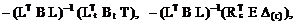
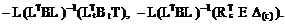
14. Какой смысл имеют элементы матрицы L? Сколько строк и столбцов имеет эта матрица? Как формируется матрица внутренней податливости сооружения В? Из каких блоков она состоит? Какой размер имеет эта матрица?

15. Какие блоки можно исключить из матриц L и В в случае, когда производится расчёт статически неопределимых рам и балок на температурные и кинематические воздействия.

16. Перепишите матричные соотношения, приведенные в п. 13, для расчёта статически неопределимых шарнирно-стержневых систем (ферм) на температурные и кинематические воздействия. Какой смысл в этом случае будут иметь элементы матриц L и L_t? Каким образом будут вычисляться элементы матриц В и B_t для шарнирно-стержневых систем?

17.8. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 6. Метод сил. § 6.6. Расчёт статически неопределимых систем на действие температуры и осадки опор. – С. 134–136. § 6.7. Пример расчёта статически неопределимой рамы методом сил. – С. 140–142.

2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дар­ков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.

Гл. 6. Расчёт статически неопределимых систем методом сил. § 6.4. Расчёт статически неопределимых систем на действие температуры. § 6.5. Составление канонических уравнений при расчёте систем на перемещения опор. – С. 213–219.

3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащени­ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. XI. Метод сил. § 63. Некоторые свойства статически неопределимых систем. Расчёт на действие температуры и осадку опор. – С. 361–368.

4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. IX. Расчёт рам методом сил. § IX.4. Расчёт рам на тепловое воздействие и смещение опор. – С. 162–166.

5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.

Гл. 5. Расчёт сооружений методом сил. § 5.3. Тепловое воздействие. – С. 57–65. § 5.4. Кинематическое воздействие. – С. 69–75.

Лекция восемнадцатая