Вынос в натуру проектной плоскости

Для разбивки в натуре в натуре проектной плоскости можно использовать различные методы.

Разбивку плоскости с небольшим проектным уклоном можно выполнить наклонным лучом нивелира (при больших уклонах теодолитом). Для этого ось вращения нивелира устанавливают перпендикулярно проектной плоскости, тогда визирная ось трубы при вращении нивелира будет описывать плоскость, параллельную проектной, на расстоянии, равном высоте инструмента.

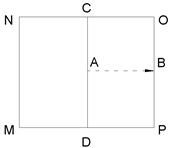
Рис. 3.7.1. Вынос в натуру проектной плоскости

Допустим, что на местности необходимо разбить плоскость MNOP с проектным уклоном, направление которого на рисунке показано стрелкой AB (рис. 3.7.1.). На местность переносят точки A, B, C и D с проектными отметками, соответствующими заданному уклону плоскости, и закрепляют их колышками. Очевидно, что точки C и D должны иметь одинаковые отметки. Затем в точке A устанавливают нивелир и приводят его в рабочее положение. При этом один подъемный винт нивелира располагают по линии AB, а два других – по линии CD. Измерив высоту прибора I, откладывают ее на рейке, установленной в точке B. Подъемным винтом, расположенным по линии AB, направляют визирную ось трубы нивелира на отсчет по рейке, равный высоте прибора i. В этом случае вертикальная ось вращения нивелира будет перпендикулярна проектной плоскости. Для контроля правильности установки нивелира берут отсчеты по рейкам в точках C и D. Они должны быть равны высоте прибора i.

Для детальной разбивки проектной плоскости на каждой выбранной точке забивают колья так, чтобы отсчет по рейке, поставленной на эти колья, был равен высоте прибора. При этом способе разбивки в пределах проектной плоскости MNOP можно выставить колья в любом количестве, без дополнительных вычислений и измерений.

При планировочных работах на больших территориях целесообразно применять метод управления лазерным лучом. Он заключается в управлении работой планировочных машин и механизмов с помощью опорных лазерных лучей или плоскостей (3.7.2.).

Принцип действия систем для контроля планировочных работ и управления рабочими органами строительных машин и механизмов состоит в создании на местности световой опорной горизонтальной или наклонной линии либо плоскости. Приемное устройство устанавливают на рабочем органе землеройной машины и определяют положение механизма относительно световой линии или плоскости. Информация, поступающая от приемного устройства, используется для ручного, полуавтоматического управления рабочим органом землеройной машины.

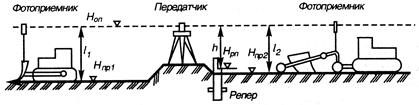
Рис. 3.7.2. Геодезический контроль планировочных работ с помощью лазерной системы.

3.8.Разбивка на местности круговых кривых

При строительстве линейных сооружений, при возведении отдельных зданий, имеющих закругленные части, возникает необходимость разбивки на местности круговых кривых. Разбивка кривой выполняется в два этапа: разбивка главных точек кривой и детальная разбивка кривой.

На первом этапе получают положение главных точек кривой (рис. 3.8.1.), то есть начала кривой (НК) A, конца кривой (КК) C и середины кривой (СК) M.

Для получения этих точек необходимо знать угол поворота 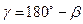, радиус кривой R, длину касательной AB = BC = T, называемую тангенсом, длину кривой AMC = K, биссектрису BM = Б, домер D.

Угол β измеряется на местности теодолитом в точке B, радиус R назначается применительно к техническим нормативам для проектирования сооружения.

Зная γ и R, остальные элементы вычисляются по формулам

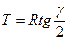; (3.8.1.)

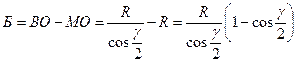; (3.8.2.)

Или 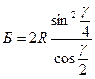; (3.8.3.)

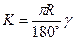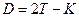; . (3.8.4.)

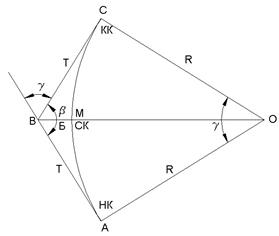
Рис. 3.8.1. Схема разбивки главных точек кривой

На практике все элементы кривой выбираются из специальных таблиц по аргументам γ и R.

Отложив на местности от вершины угла поворота B отрезки 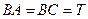, а вдоль биссектрисы угла β отрезок Б, получим начало кривой (НК), конец кривой (КК) и средину кривой (СК).

На следующем этапе выполняют детальную разбивку кривой.

Для этого между главными точками кривой разбивают промежуточные через

20 м при R > 500 м;

10 м при 100 < R ≤ 500 м;

5м при R ≤ 100 м.

Существует несколько способов детальной разбивки кривых. Рассмотрим один из способов – способ прямоугольных координат (рис. 3.8.2.).

В этом способе положение точек P₁, P₂, P₃ определяется через равные дуги k координатами x₁, y₁; x₂, y₂; x₃, y₃; …, при этом за ось абсцисс принимают линию тангенса, за начало координат – начало или конец кривой.

Рис. 3.8.2. Схема детальной разбивки кривой

Для вычисления координат задавшись значением длины дуги k вычисляют угол φ

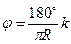. (3.8.5.)

Затем вычисляют координаты точек по формулам

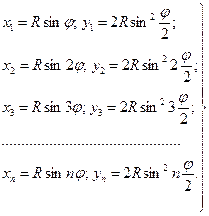(3.8.6.)

Разбивку кривой ведут от начала и конца кривой к середине. Абсциссы и ординаты откладывают по касательной и перпендикулярно ей при помощи рулетки или ленты. Перпендикуляры строят экером или теодолитом. Координаты, вычисленные по формулам, на практике определяют при помощи таблиц для разбивки кривых.