Расчет надежности резервированной системы с параллельным включением элементов

Для повышения надежности системы применяют резервирование. Обычно это – параллельное соединение элементов в системе, из которых часть являются резервными. Например, это насосная станция, состоящая из 4 параллельно соединенных насосов, из которых два насоса рабочие, а два насоса – резервные.

Основным параметром резервирования является его кратность. Пусть n – общее число элементов в системе, а m – число элементов, необходимых для нормальной работы системы. Под кратностью резервирования r понимается отношение числа резервных элементов к числу основных:

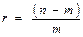(39)

Бывает резервирование с целой кратностью, когда величина r есть целое число (в этом случае всегда m = 1), и резервирование с дробной кратностью, когда r есть дробное несокращаемое число. Например,

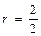– есть резервирование с дробной кратностью.

1). При резервировании с постоянно включенным резервом и с целой кратностью вероятность безотказной работы системы определяется по формуле:

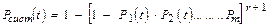(40),

где Р_i(t) – вероятность безотказной работы отдельного i - го элемента системы в течение времени t .

Если все элементы системы одинаковы, то при экспоненциальном законе надежности получаем

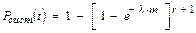(41),

а среднее время наработки системы на отказ

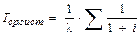(42).

где l – интенсивность отказа отдельного элемента. Например, при n = 3 и m = 1 получаем

;

.

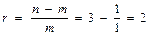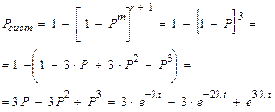
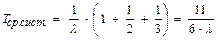2). При резервировании с постоянно включенным резервом и дробной кратностью получаем следующие формулы:

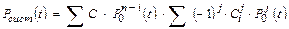(43)

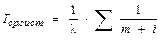(44),

где Р_о(t) – вероятность безотказной работы отдельного элемента системы, С_i^j – число сочетаний из i элементов по j. Например, при n = 4 и

;

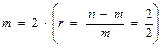Получаем:

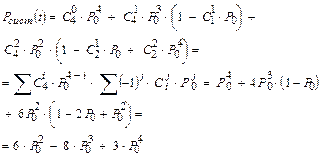
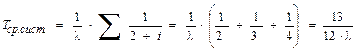
3). В случае отсутствия резервирования (r = 0), когда к отказу системы приводит отказ любого из ее элементов, получаем:

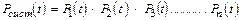(45)

Для одинаковых элементов и при экспоненциальном законе надежности:

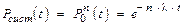(46)

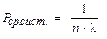(47)

В целом можно показать, что для всех указанных случаев можно составить таблицу, например, для системы, состоящей не более чем n=5 однотипных элементов, при любых требованиях, накладываемых на возможные состояния их работы (работа m элементов из n), где каждая клетка таблицы дает формулу для вычисления вероятности безотказной работы соответствующей системы.

Таблица 8

m	Значения Рсист при общем числе n элементов в системе
n=1	n=2	n=3	n=4	n=5
	Р0	2Р0-Р02	3Р0-3Р02+Р03	4Р0-6Р02+4Р03-Р04	5Р0-10Р02+10Р03-5Р04+Р05
	-	Р02	3Р02-2Р03	6Р02-8Р03+3Р04	10Р02-20Р03+15Р04-4Р05
	-	-	Р03	4Р03-3Р04	10Р03-15Р04+6Р05
	-	-	-	Р04	5Р04-4Р05
	-	-	-	-	Р05

В первой строке таблицы даны формулы для определения надёжности комбинации параллельно включённых элементов, т.е. систем, для работы которых достаточно исправного состояния одного из всех имеющихся элементов. Эти выражения получены по формуле Р=(1–р)^п. На главной диагонали таблицы располагаются значения надёжности комбинаций последовательно включённых элементов, эти значения определяются по формуле Р=р^п. Во всех остальных ячейках приведены выражения и указаны численные значения вероятности безотказной работы сложных комбинаций, в которых для их нормального функционирования необходима и достаточна работа т из п элементов.

Надёжность системы падает с увеличением последовательно соединённых элементов и увеличивается с увеличением числа параллельно включенных элементов [2].

Задача 8.

Насосная станция состоит из n однотипных насосов, включенных параллельно, из которых m являются рабочими. Интенсивность отказов каждого из насосов l = 0,2 ^. 10 ^-3 1/час.

Необходимо определить вероятность безотказной работы насосной станции в течение t = 2000 час, а также среднюю наработку до первого отказа. Сделать то же самое для случая, когда резервирования насосов нет, сравнить полученные результаты и сделать вывод об эффективности резервирования.

При решении задачи использовать приведенные выше формулы и табл. 8. Исходные данные приведены в табл. 9.

Таблица 9

вариант	Последняя цифра шифра студента
n
m