Аналитическое определение количественных характеристик надежности
Количественные характеристики надежности определяются по следующим формулам
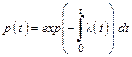 (8)
(8)
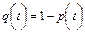 (9)
(9)
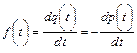 (10)
(10)
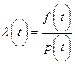 (11)
(11)
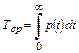 (12)
(12)
где p(t) – вероятность безотказной работы изделия на интервале времени от 0 до t; q(t) – вероятность отказа изделия на интервале времени от 0 до t; f(t) – частота отказов изделия или плотность вероятности времени безотказной работы изделия Т; λ(t) – интенсивность отказов изделия; Тср – среднее время безотказной работы изделия.
Для систем водоснабжения и водоотведения, как правило, принимают экспоненциальный закон распределения случайной величины. Однако из теории восстановления известно, что экспоненциальное распределение неприменимо для систем, в которых существенны явления старения (что несправедливо для систем ВиВ). Кроме того, для систем, имеющих экспоненциально распределенную наработку, выполнять планово-предупредительные замены нецелесообразно, что противоречит нашим представлениям об эксплуатации систем ВиВ [3]. Поэтому принимать экспоненциальную наработку возможно лишь только при следующих условиях:
– при исследовании безотказности на относительно малых интервалах времени в предположении о классической схеме эксплуатации систем ВиВ, состоящей из трех этапов, (рис. 2);
– при исследовании безотказности большого числа элементов, например, систем водоснабжения города.
Формулы (8) – (12) для экспоненциального закона распределения времени безотказной работы изделия примут вид
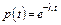 , (13)
, (13)
при λt<<1 формула (13) примет вид 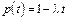
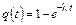 (14)
(14)
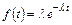 (15)
(15)
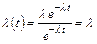 (16)
(16)
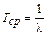 (17)
(17)
Формулы (8) – (12) для закона распределения Релея времени безотказной работы изделия имеют вид
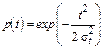 (18)
(18)
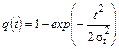 (19)
(19)
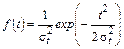 (20)
(20)
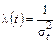 (21)
(21)
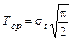 (22)
(22)
где σt – мода распределения случайной величины Т; Т – время безотказной работы изделия.
Задача. 4.
Определить суммарное значение интенсивности отказов λс и вероятности безотказной работы через 100, 1000, 2000, 4000, 8000 ч непрерывной работы. Принципиальная схема рассматриваемой системы приведена на рис.3. Снижение вероятности безотказной работы менее 0,7 считать отказом системы. Если предпоследняя цифра зачётной книжки от 0 – 4, то студент принимает стальные трубы, если от 5 – 9 – чугунные.
Значение интенсивности отказов отдельных элементов санитарно-технических систем приведены в приложении (табл. П1). Исходные данные к задаче приведены в табл. 4.
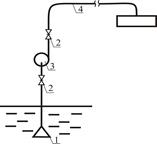 1 – приёмный клапан;
1 – приёмный клапан;
2 – задвижка;
3 – насос;
4 – трубопровод.
Рис. 3.Расчётная схема
Таблица 4
| Вариант | L, см | Диаметр трубопровода, мм | Марка насоса |
| ЭЦВ 4 | |||
| ЭЦВ 6 | |||
| ЭЦВ 8 | |||
| ЭЦВ 10 | |||
| ЭЦВ 6 | |||
| ЭЦВ 10 | |||
| ЭЦВ 4 | |||
| ЭЦВ 8 | |||
| ЭЦВ 6 | |||
| ЭЦВ 8 |
Методические указания к решению задачи 4.
При анализе статистических данных об отказах отдельных элементов, составляющих систему, установлено, что значение интенсивности отказов λ колеблется в пределах от λmax до λmin. В этом случае вероятность безотказной работы будет иметь вид, представленный на рис. 4.
Расчёт надёжности целесообразно производить в следующей последовательности: рассматривается принципиальная схема, устанавливается связь между отдельными элементами системы, сложные системы разбиваются на подсистемы, которые в свою очередь на группы, узлы, составляется структурная схема, составляется таблица расчёта надёжности, по данным таблицы рассчитываются количественные показатели надёжности блоков, подсистем, и системы в целом.
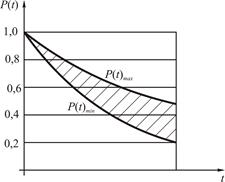
Рис.4.Зависимость р(t) от времени
В принципиальных (функциональных) схемах показываются реальные связи между элементами системы: электрические, кинематические и др. Каждый элемент этой системы показывает конкретную технологическую принадлежность.
В структурных схемах показывают лишь те связи, которые отражают надёжность системы, при выполнении заданных функций.
Задача 5.
(если последняя цифра зачётной книжки от 0 до 4) время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром λ. Определить количественные характеристики надёжности: вероятность безотказной работы, вероятность отказа, частоту отказов и среднее время безотказной работы для времени t. Исходные данные для задачи принять по табл. 5.1.
(если последняя цифра зачётной книжки от 5 до 9) время работы элемента до отказа подчинено закону распределения Релея. Требуется вычислить количественные характеристики надёжности элемента: вероятность безотказной работы, частоту отказа, интенсивность отказа, среднее время безотказной работы для времени t, если параметр распределения σ. Исходные данные для задачи принять по табл. 5.2.
Таблица 5.1
| Варианты | ||||||||||
| λ·104, 1/ч | 1,5 | 0,8 | 1,9 | |||||||
| t, ч |
Таблица 5.2
| Варианты | ||||||||||
| σ, ч | ||||||||||
| t, ч |
