Расчёт длины кривой свободной поверхности на водоскате быстротока

h, м

, м2

, м

, м

_ , м

, м0,5/с

_ , м0,5/с

, м/с

_ , м/с

, м

, м

, м

, м

h1

–

–

–

–

–

–

–

–

–

–

–

–

h2

–

–

–

–

–

–

–

–

–

–

–

–

–

h3

–

–

–

–

–

–

–

… … … …

hп

–

–

–

–

–

–

–

2) , т.к. лоток прямоугольной формы и коэффициент откоса ;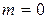

3) , т.к. лоток прямоугольной формы и коэффициент откоса ;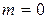

4) ;

5) , где и – гидравлические радиусы, соответствующие соседним глубинам;

6) , где – коэффициент шероховатости с учётом аэрации потока;

7) , где и – коэффициенты Шези, соответствующие соседним глубинам;

8) , где 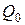– заданный расход воды, поступающий из подводящего канала;

9) , где и – средние скорости в соседних сечениях;

10) ;

11) , где – удельная энергия соответствующих сечений;

12) , где и – удельные энергии соседних сечений, причём в последующем сечении для данного типа кривой спада удельная энергия сечения больше, чем в предыдущем;

13) ;

14) , т.к. расчёт кривой свободной поверхности начинается с точки излома дна; последующие числовые значения длин
, , … определяются путём наращивания, а именно: , и т.д.

Назначение глубин для расчёта кривой свободной поверхности будет правильным, если при вычислении приращения длины (столбец 13 в табл. 7) не появятся отрицательные значения.

3.2.5. Построение кривой свободной поверхности
на водоскате быстротока

Построение кривой свободной поверхности выполняется на миллиметровой бумаге формата А4 или А3 в следующих масштабах: вертикальный – 1:10, горизонтальный – свободный стандартный, но предполагающий достаточную точность (1,0 м) при определении длины участка при соответствующей глубине (1:100, 1:200, …).

Кривая свободной поверхности строится в виде графика с вертикальной осью глубин и горизонтальной осью длин (рис. 11).

На графике обязательно указываются линии критических К–К и нормальных N–N глубин. Отдельные значения глубин и длин по осям отмечать не следует, чтобы не загромождать график. Для построения кривой свободной поверхности точки на графике соединять плавно по лекалам.

Рис. 11. Пример построения графика кривой

свободной поверхности

Используя график свободной поверхности, необходимо принять глубину в конце быстротока.

В большинстве случаев длины призматических русел бывают достаточными, чтобы на них успевал устанавливаться равномерный режим и отвечающая ему нормальная глубина потока h₀. Для назначения требуемой глубины (в курсовой работе длина быстротока l – величина заданная) придерживаются следующих условий:

– если длина быстротока равна или больше длины кривой спада, то глубину на конце быстротока принимают равной нормальной глубине ;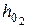

– если же, наоборот, длина кривой спада будет больше длины быстротока, то глубина на конце быстротока определяется по графику: на горизонтальной оси длин откладывается значение длины быстротока (см. подразд. 2.2), поднимается вертикаль до пересечения с кривой, слева на вертикальной оси глубин снимается значение .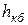

Отводящий канал

Для защиты от размыва низового откоса земляного полотна дороги и выходной части водопропускного сооружения часто устраивают водоотводные искусственные русла, по своей конструкции мало отличающиеся от подходных русел. Вода, выходящая из отверстия сооружения, часто обладает ещё большой энергией, т.е. повышенной против его естественного состояния разрушительной силой. Опыт эксплуатации водопропускных сооружений показывает, что если не предусмотреть специальных мер, отводные русла на выходе из сооружений сильно размываются, что иногда приводит к авариям сооружений.

Мерами против размывов водоотводных русел, т.е. способами гашения энергии водного потока, являются: непрерывное рассеивание энергии потока в самом сооружении, сосредоточенное гашение энергии потока на выходе из трубы, укрепление отводных русел.

Известно много различных принципов гашения энергии потока. Наиболее распространенные из них:

1) усиленное перемешивание (этот принцип используется при устройстве повышенной шероховатости поперечных расщепляющих балок, зубчатых порогов);

2) соударение свободных струй в атмосфере;

3) рассеивание энергии в вальцах гидравлического прыжка;

4) сосредоточенное гашение энергии в замкнутом блоке – напорные гасители;

5) отброс струи от сооружения с одновременным их расщеплением и аэрацией (этот принцип реализуется в рассеивающих трамплинах);

6) силовое воздействие на поток в направлении, противоположном течению, путём установки различных препятствий: порогов, шашек, пирсов и т.п.

В данной курсовой работе студентам предлагается при расчёте комплекса водоотводных сооружений выяснить условие сопряжения бьефов быстротока и отводящего канала. Для анализа необходимо определить нормальную и критическую глубины на третьем участке водоотвода, а также соответствующий критический уклон.

По полученным данным выполнить расчёт возникающего гидравлического прыжка и сделать вывод о необходимости устройства гасителя энергии с последующим его расчётом.