Для внеаудиторной работы к практическим занятиям
СБОРНИК
МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ
ДЛЯ ВНЕАУДИТОРНОЙ РАБОТЫ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
по дисциплине «Доказательная медицина»
для студентов ФФМО
Красноярск
Занятие №1
Занятие №2
Тема: «Основы теории вероятности»
В соответствии с концепцией доказательной медицины в большинстве случаев диагноз, прогноз и результаты лечения для конкретного больного не могут быть определены точно и потому должны быть выражены через вероятности. Эти вероятности для конкретного больного лучше всего оценивать на основе предыдущего опыта, накопленного в отношении групп аналогичных больных. Таким образом, характерной чертой доказательной медицины является использование вероятностного подхода к оценке различных явлений.
Теория вероятностей — математическая наука, устанавливающая закономерности случайных явлений.
Закономерности, устанавливаемые теорией вероятностей, позволяют по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.
Вероятность — это возможность реализации какого-либо события, например, выздоровления или смерти. Когда речь идет о вероятности, используются соответствующие термины:
Эксперимент – процесс измерения или наблюдения с целью сбора данных. Примером является кидание костей или оценка исходов лечения.
Событие (исход) – определенный результат эксперимента. Примером является факт одновременного выпадения двоек, троек, четверок или пятерок на обеих костях. Для медицины примером может служить оценка результатов при выписке пациентов: излечение или хронизация заболевания, выявление заболевания у наугад выбранного человека при проведении профилактического осмотра. Под событием в теории вероятностей понимается всякий факт, который при реализации определенного комплекса условий может произойти или не произойти.
Выборочное пространство – все возможные исходы эксперимента. Если рассматривать пример с двумя игральными костями и подсчитывать сумму выпавших значений, то выборочное пространство для нашего эксперимента — это множество {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Чтобы правильно определить вероятность, необходимо решить, о какомтипе вероятности идет речь.
Под вероятностью события понимается численное выражение возможности появления данного события при реализации определенных условий.Например, вероятность выпадения «орла» или «решки» при бросании монетки равна 0.5.
При введении понятия вероятности мы опираемся на практический смысл, а именно: на основании опыта считаем более вероятными те события, которые происходят чаще, и менее вероятными те, которые происходят реже. Равновероятные события – события, которые происходят с одинаковой частотой, ни одно из них не является объективно более возможным, чем другие. Например, выпадение «орла» или «решки» при бросании монетки; выбор белого или черного шара из урны, в которой находится одинаковое число черных и белых шаров.
Случайная величина– величина, которая при реализации определенных условий может принимать различные значения. Пример: число вызовов, поступающих на станцию скорой помощи в течение суток.
Достоверное событие – событие, которое при реализации определенныхусловий произойдет в любом случае. Пример: неизбежная смерть человека при приеме токсической дозы цианистого калия или падение любого предмета вниз под действием силы тяжести.
Если приписать достоверному событию вероятность, равную 1, то вероятности всех других событий, возможных, но не достоверных, будут определяться числами от 0 до 1.
Противоположностью по отношению к достоверному событию является событие невозможное.
Невозможное событие– событие, которое при реализации определенных условий произойти не может. Пример: падение брошенного под действием силы тяжести предмета на потолок, а не на пол, илирегенерация утраченных конечностей.
Основные теоремы теории вероятности
Теорема умножения
Вероятность произведения двух событий А и В равна произведению вероятности одного из них (А) на условную вероятность другого (В), вычисленную при условии, что первое имело место.
Символически это записывается следующим образом:
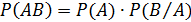
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Следствие 2. Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Как уже говорилось, под произведением событий понимается совместное их появление.
Для двух событий по теореме умножения имеем:
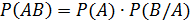
Но поскольку события независимы, справедливо равенство Р(В/А) = Р(В), и тогда получаем: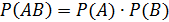 
Для трех событий по аналогии получаем: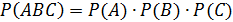 
Пример. Из урны, в которой находятся 1 черный и 2 белых шара (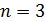 
), выбираем два шара подряд. Какова вероятность того, что оба шара белые?
Решение.Обозначим интересующее нас событие через А, а события, заключающиеся в выборе белого шара первый и второй раз — через A1 и А2, соответственно. Интересующее нас событие равно произведению событий A1 и А2: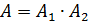 
.
По теореме умножения имеем: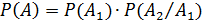 
.
Так как всего шаров три и из них два белых, то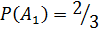 
.
Так как после появления события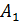 
(после выбора белого шара первый раз) осталось всего два шара, из них белых – один, то 
.
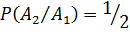Тогда:
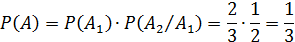
Если после выбора белого шара первый раз его возвращают в урну, то события 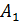и 
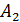будут независимыми и равными:
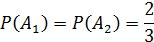
Тогда искомая вероятность будет равна:
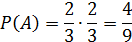
Схема испытаний Бернулли
Со схемой испытаний Бернулли связано установление важных закономерностей теории вероятностей как математической науки, относящихся к сумме независимых случайных величин и представляющих закон больших чисел. Физическим содержанием закона больших чисел является устойчивость некоторых средних в массовых случайных явлениях. В узком смысле под законом больших чисел в теории вероятностей понимается ряд математических теорем, устанавливающих факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Важные теоремы, составляющие закон больших чисел, впервые были выведены для схемы испытаний Бернулли.
Теорема Чебышева. Среднее арифметическое наблюдаемых значений случайной величины при достаточно большом числе испытаний приближается к ее математическому ожиданию.
Теорема Бернулли. Частота случайного события при достаточно большом числе независимых испытаний в неизменных условиях приближается к вероятности его появления в отдельном испытании.
Теорема Пуассона. Частота случайного события при достаточно большом числе независимых испытаний приближается к среднему арифметическому вероятностей его проявления в отдельных испытаниях.
Центральная предельная теорема. Закон распределения суммы достаточно большого числа слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму, приближается к нормальному закону распределения.
Занятие №3
То есть, владея методами статистики, мы можем с одной стороны проанализировать имеющиеся данные, с другой – предвидеть дальнейшее развитие ситуации, учесть влияние возможных факторов и выбрать оптимальное решение, влияющее на развитие ситуации.
Объектом наблюдения описательной статистики является статистическая совокупность, состоящая из отдельных предметов или явлений – единиц наблюдения, взятых в определённых границах времени и пространства. Они объединены общей связью, но различаются по ряду варьирующихся признаков.
Единица наблюдения– первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих изучению.
Статистическая совокупность, подлежащая исследованию, называется генеральной совокупностью. Теоретически генеральная совокупность может быть безгранична.
Выборочная совокупность (выборка) – подмножество (часть) генеральной совокупности, получаемое посредством случайного отбора. Смысл выборочного метода состоит в том, что извлечение из некоторой весьма пространной (или вообще беспредельной) генеральной совокупности несравненно меньших по объему выборок резко экономит время обработки данных. Процесс случайного отбора данных называется процессом рандомизации(random – «случайный»).
Важность принципа рандомизации (случайного отбора) можно проиллюстрировать следующим образом. Представим, что необходимо собрать образцы определенного вида растений с какой-то гигантской площадки (поля) с целью описать некие их свойства. Например, подсчитать среднее число зерен в колосе какого-то злака. Совокупность экземпляров данного вида, произрастающая на данном поле, и будет составлять генеральную совокупность. Понятно, что, если поле действительно очень большое, то в разных его частях система природных факторов, влияющих на рост и развитие растений, будет складываться несколько иначе: будет сказываться разница в структуре почвы, рельефе, глубине подпочвенных вод, осадках, удаленность от дороги или лесной опушки и т.д. В результате, как это действительно и происходит на практике, в разных местах поля колосья заведомо будут различны, поэтому если вы будете собирать образцы лишь с одного чем-то лично вам понравившегося участка (например, «далеко ходить не надо» или другие личные мотивы), то практически гарантированно вы получите искаженные сведения о генеральной совокупности. Действительно, ведь вам будут, как правило, попадаться объекты, у которых интересующее вас свойство будет содержаться либо «в избытке», либо «в недостатке». Иными словами, вы внесете в данные некую нарочитую тенденцию, вольно или невольно вызовите их смещение в сторону относительно высоких ли низких значений по отношению к их действительному состоянию в генеральной совокупности. Понятно, что такой подход, независимо от того, какие объекты вас действительно интересуют (растения, животные, люди), может привести к неверным заключениям и прогнозам со всеми вытекающими последствиями. При этом совершенно неважно, внесены ли такие ошибки сознательно или непроизвольно, из самых лучших побуждений («чтобы было как лучше») или, наоборот, из желания «навредить». Рандомизация же (возвращаясь к примеру с растениями на поле) действует как механизм, позволяющий вам независимо от вашего желания-нежелания более или менее равновероятно «выдергивать» образцы из самых разных участков генеральной совокупности. Это обеспечивает нивелирование действия специфических локальных факторов на изучаемые объекты («избытки» в одном месте компенсируются «недостатками» в другом), благодаря чему свойства рандомизированной выборки приближаются к реальным свойствам генеральной совокупности.
Репрезентативность выборочной совокупности– свойство выборки корректно отражать генеральную совокупность.
Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей. Например, выборка, целиком состоящая из пациентов, больных сахарным диабетом, не репрезентирует всех пациентов больницы, но может отлично отображать пациентов-диабетиков.
Выделяют репрезентативность количественную и качественную (структурную). Количественная репрезентативность определяется числом наблюдений, гарантирующим получение статистически достоверных данных. В общем, здесь действует основной постулат закона больших чисел — «чем больше наблюдений — тем результаты достоверней» или «чем больше число наблюдений, тем больше значения характеристик выборки приближаются к соответствующим характеристикам генеральной совокупности».
Качественная репрезентативность — обозначает структурное соответствие выборочной и генеральной совокупностей. Например: если в составе генеральной совокупности 50% — лица мужского пола, то и в выборочной группе их должно быть 50%.
В силу закона больших чисел выборка будет качественно репрезентативной только в том случае, если ее осуществить случайно. Проводить отбор случайно – значит обеспечить выполнение условия, что каждый объект выборки отбирается случайно из генеральной совокупности.
Для каждого объекта (единицы наблюдения) регистрируют один и тот же признак или признаки. Например, регистрируется рост и масса людей; численность населения, уровень рождаемости и смертности для городов; объем памяти и т.д. Признак, который регистрируется для каждого из объектов, называют переменной.
Наборы данных классифицируют по следующим признакам:
· по количеству переменных (одномерные, двумерные или многомерные наборы данных);
· по типу данных (количественные или качественные);
· по тому, важна ли упорядоченность данных во времени или нет.
Одномерные наборы данных содержат только один признак для каждого объекта. Эти данные позволяют определить типичное значение признака – то, насколько значения отличаются друг от друга, требуют ли отдельные данные особого внимания. Примером одномерных данных является информация о средней рождаемости в стране по регионам. Она позволяет назвать регионы с самым высоким и с самым низким уровнем рождаемости.
Двумерные наборы данных содержат информацию о двух признаках для каждого из объектов. Кроме того, что они дают возможность получить два набора одномерных данных. Двумерные данные также позволяют установить, существует ли связь между двумя переменными, насколько сильно связаны переменные, можно ли предсказать значение одной переменной по значению другой и если да, то с какой надежностью. Например, данные опроса студентов о том, удовлетворены ли они уровнем теоретической и практической подготовки, получаемой в вузе (значения обеих переменных записываются в виде да/нет или 1/0), позволяют установить, есть ли связь между уровнями теоретической и практической подготовки.
Многомерныеданные содержат информацию о трех или более признаках для каждого объекта. В дополнение к той информации, которую можно извлечь из одномерных и двумерных наборов, многомерные данные можно использовать для получения информации о том, существует ли простая зависимость между этими признаками, насколько они взаимосвязаны (речь идет не только о попарной взаимосвязи признаков, но и о зависимости в совокупности), можно ли предсказать значение одной переменной на основании значений остальных.
Признаки,или переменные, могут принимать различные конкретные значения. Различают следующие виды признаков:
Качественныеили номинальные– признаки, не поддающиеся непосредственному измерению (номинальная шкала). Состоит из взаимоисключающих категорий. Например, характеристики пациента: диагноз, пол, профессия, семейное положение. Пример: семейный статус – холост, женат, разведен, вдовец; вид заболевания – астма, бронхит, пневмония.
Качественные данные, которые могут быть отнесены только к двум противоположным категориям «да» – «нет», принимающие одно из двух значений (выжил – умер; курит – не курит), называются дихотомическими (бинарными). Даже если значениям качества можно приписать числа (например, полу человека приписать соответственно числа 0 и 1), то обрабатывать эти числа как количественные данные нельзя.
Порядковыеили ранжируемые – признаки, которые можно расположить в естественном порядке (ранжировать), но при этом отсутствует количественная мера расстояния между величинами. Примером являются оценка тяжести состояния пациента, стадия болезни, самооценка состояния здоровья. При этом допускается, что тяжелое течение заболевания «хуже», чем среднетяжелое, а очень тяжелое – «еще хуже», однако нельзя сказать во сколько или на сколько хуже. Можно сказать, что порядковые данные занимают промежуточное положение между количественными и качественными типами. Их можно упорядочить как количественные данные, но над ними нельзя производить арифметические действия, как и над качественными данными.
Количественныеили интервальные – признаки, количественная мера которых четко определена. Это наиболее удобный для статистического анализа тип данных.
Количественные признаки могут быть:
- непрерывными– принимающими любое значение на непрерывной шкале; например: масса тела, температура, биохимические показатели крови;
- дискретными– принимающими значения лишь из некоторого списка определенных чисел, обычно целых; например: число рецидивов, число детей в семье, число заболеваний у одного больного, число выкуриваемых сигарет, число вызовов "скорой помощи", поступающих в больницу.
По роли в статистической совокупности учетные признакиможно подразделить на факторные(факториальные) и результативные(результирующие) признаки.
Результативный признак — зависимый, изменяющий свое значение под влиянием другого, связанного с ним и действующего на него факторного признака. Например: количество выкуренных сигарет – факторный признак, вероятность возникновения заболевания легких и сердца – результативный признак. Ролевая значимость этих признаков иногда может меняться. Например: концентрация инсулина в крови и концентрация сахара крови. Высокий уровень сахара крови вызывает усиленный выброс инсулина в кровь. В то же время повышение концентрации инсулина ведет к снижению сахара крови. Так же как реализация скрининг исследований инфекционных заболеваний влияет на своевременность выявления, снижение риска инфицирования и числа зараженных (это впоследствии уменьшает эффективность скрининга и целесообразность его проведения).
Все единицы наблюдения, относящиеся к одной статистической совокупности, имеют некоторое число общих учетных признаков, свидетельствующих о принадлежности конкретной единицы наблюдения к этой совокупности. Такие признаки называются признаками сходства (место работы, время работы на предприятии, место жительства и т.п.). Эти признаки описывают обязательное условие статистического наблюдения: единство места и времени исследования.
Признаки различия представляют индивидуальные особенности (характеристики) каждой единицы наблюдения. В медицинских исследованиях это могут быть пол, возраст, производственный или профессиональный стаж, заболеваемость и т.п. Строго говоря, признаки различия и являются конечным объектом статистического исследования.
Многие статистические данные получают в процессе измерений. Целью измерений является получение информации о признаках объектов, организмов, событий. Измеряется не сам объект, а только свойства или отличительные признаки объекта. Например, измеряется не ребенок, а его рост и масса. Измерения осуществляются путем установления соответствия между числами и объектами, которые являются носителями подлежащих измерению свойств. Измерения могут проводиться на разных уровнях. Различным уровням измерений соответствуют различные шкалы:
1) номинальная шкала;
2) порядковая, или ранговая, шкала;
3) шкала интервалов;
4) шкала отношений, или шкала пропорций;
5) логарифмическая шкала.
Номинальная шкала используется для регистрации самого низшего уровня измерений, предполагающего наличие минимальных предпосылок для измерения. При измерениях на данном уровне практически не используются числа. Здесь важно установить подобие или различие объектов по некоторому признаку. Например, распределение жителей по половому признаку. С помощью подсчета можно установить число мужчин и женщин в каждом регионе.
Порядковая, или ранговая, шкала указывает лишь последовательность носителей признака или направление степени выраженности признака.
Например, учащихся можно ранжировать по количеству правильно выполненных тестовых заданий. Пусть учащиеся А, Б, В, Г, Д правильно выполнили соответственно 21, 16, 12, 9 и 3 задания. Графически это можно изобразить так:
Эта порядковая шкала имеет величины от 1 до 5, и учащиеся на ней размещены в зависимости от количества правильно выполненных заданий: А – первый, Д – пятый. Из рисунка видно, что интервалы, разделяющие места в ряду, различны по величине. По этой причине нецелесообразно складывать, вычитать, умножать и делить порядковые места.
Шкала оценок по одному предмету является порядковой шкалой, так как интервалы между отдельными баллами не отражают разрыва между реальными результатами. Мы знаем только, что ученик, получивший оценку "5" по какому-то предмету, знает этот предмет лучше того, кто получил "4". Но нельзя утверждать, что различие в знаниях этих учащихся такое же, как и в знаниях тех, кто получил "4" и "3". Так как шкала оценок является порядковой шкалой, то некорректно выставлять итоговую оценку как среднюю арифметическую текущих оценок.
На шкале интервалов равные интервалы отображают одинаковую меру величины измеряемого признака. Например, 1оС между 23оС и 24оС на шкале Цельсия имеет такой же смысл, как и 1оС между 11оС и 12оС. Другими словами, на шкале интервалов расстояния между соседними делениями равны. На интервальной шкале вполне осмысленным является вопрос "на сколько?". Но, пользуясь интервальной шкалой, нельзя сформулировать вопрос "во сколько раз?". Дело в том, что на шкале интервалов устанавливаются произвольно начало отсчета (нуль шкалы), единица измеренияинаправление отсчета. Примером интервальной шкалы является температурная шкала по Цельсию. Разность между температурами воздуха +30 и +20°С столь же велика, как и между -10 и -20°С. Однако, нельзя утверждать, что при температуре воздуха +30°С в полтора раза теплее, чем при температуре +20°С. Даже если температура воздуха равна 0°С, нельзя утверждать, что тепла нет совсем: ведь начало отсчета выбрано произвольно.
Также шкалой интервалов является шкала коэффициента интеллекта IQ.
Шкала интервалов является метрической, с ее помощью можно выполнять сложение и вычитание. Она имеет значительные преимущества по сравнению с номинальной и порядковой шкалами.
Шкала отношений, или шкала пропорций, кроме равенства интервалов между соседними делениями шкалы, также дает возможность устанавливать отношения значений измеряемого признака. Это возможно благодаря тому, что значению шкалы "0" соответствует величина, для которой измеряемый признак отсутствует. Другими словами, начало отсчета на этих шкалах выбирают непроизвольно. Примерами шкалы отношений являются меры длины (м, см и т.д.) и массы (кг, г и т.д.). Предмет длиной 100 см вдвое длиннее предмета длиной 50 см.
Важно упомянуть о логарифмической шкале. Иногда данные нуждаются в преобразованиях. В частности, потребность в этом возникает, когда в ряду данных одно или несколько значений существенно превышают остальные. Если данные явно несимметричны, то каждое значение приведенного набора данных заменяют логарифмом этого значения с целью упростить статистический анализ. Логарифмирование преобразует "скошенные" (асимметричные) данные в более симметричные, так как происходит "растягивание" шкалы возле нуля. При этом малые значения, сгруппированные вместе, распределяются вдоль шкалы. В то же время логарифмирование собирает вместе большие значения на правом конце шкалы. Наиболее часто применяют десятичные и натуральные логарифмы. Равным расстояниям на логарифмической шкале соответствует равные процентные увеличения на исходной шкале, а не равные увеличения значений.
Пример
В таблице представлена численность населения (в тыс. чел.) в республиках бывшего СССР в 1976 г.
| Россия | Украина | Белоруссия | Узбекистан | Казахстан |
| Грузия | Азербайджан | Литва | Молдавия | Латвия |
| Киргизия | Таджикистан | Армения | Туркмения | Эстония |
Заменим все значения их десятичными логарифмами. В нижеприведенной таблице вместо численности населения представлены их десятичные логарифмы.
| Россия | Украина | Белоруссия | Узбекистан | Казахстан |
| 8,13 | 7,69 | 6,97 | 7,15 | 7,16 |
| Грузия | Азербайджан | Литва | Молдавия | Латвия |
| 6,69 | 6,76 | 6,52 | 6,59 | 6,40 |
| Киргизия | Таджикистан | Армения | Туркмения | Эстония |
| 6,53 | 6,54 | 6,45 | 6,41 | 6,16 |
Эти данные симметрично группируются вокруг среднего значения 6,81.
Вариационный ряд – ряд числовых измерений какого-либо признака, отличающихся друг от друга по своей величине и расположенных в определенном порядке (возрастания или убывания).
Каждое числовое значение в вариационном ряду называют вариантой ( 
).При большой численности наблюдений некоторые варианты повторяются. В связи с этим в вариационном ряду принято выделять частоты (р). Частота данной варианты – это количество элементов совокупности, имеющих одинаковое числовое значение. Отношение частоты варианты к объему совокупности (или общему числу наблюдений n) назвали относительной частотой варианты и обозначили через 
, 
при этом выполняется условие v1 + v2 + ... + vk = 1.
Виды вариационных рядов:
1. В зависимости от вида случайной величины:
- дискретный;
- непрерывный.
2. В зависимости от группировки вариант:
- несгруппированный;
- сгруппированный (интервальный):
3. В зависимости от частоты, с которой каждая варианта встречается в вариационном ряду:
- простой (р =1);
- взвешенный (р>1).
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями. Наиболее часто употребляемые квантили представлены в таблице:
Средняя величина– это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
В зависимости от характера задачи пользуются тем или иным видом средней величины. К ним принадлежат среднее арифметическое, мода, медиана, степенные средние (среднее гармоническое, среднее геометрическое и т.п.).
Пусть имеется n объектов, для которых измерена некоторая характеристика, и получены значения 
, 
, ..., 
. Среднее арифметическое этих n значений обозначают через Ми определяют как
это также может быть записано следующим образом:
Медиана, или средняя точка, может быть вычислена как для порядковых, так и для количественных данных. Если все элементы совокупности размещены в порядке возрастания или убывания числовых значений признака, то медиана– это такое значение признака, которое делит всю совокупность пополам.
Итак, количество элементов совокупности, имеющих значение признака, меньшее медианы, равно количеству элементов со значением признака, большим медианы. Будем обозначать медиану символом Ме.
При нахождении медианы дискретного вариационного ряда следует различать два случая:
1) объем совокупности нечетный;
2) объем совокупности четный.
Если объем совокупности нечетный и равен (2n+1), и варианты размещены в порядке возрастания их значений:
то 
.
Если же количество элементов четное и равно 2n, то нет варианты, которая бы делила совокупность на две равные по объему части:
поэтому в качестве медианы условно берется полусумма вариант, находящихся в середине вариационного ряда:
Медиана обладает важными свойствами, которые в некоторых случаях дают ей преимущество перед другими средними величинами. Например, если при упорядоченном размещении некоторого признака "крайние" значения сомнительные и к тому же резко отличаются от основной массы данных, то в качестве меры центральной тенденции целесообразно использовать медиану. Это связано с тем, что на ее величину эти "крайние" значения никакого влияния не оказывают, а в то же время они могут существенным образом повлиять на значение среднего арифметического.
Среднее арифметическое является хорошей мерой центральной тенденции для количественных данных, не имеющих выбросов; медиана - для порядковых данных и для количественных данных, в том числе и при наличии выбросов. Подобная характеристика нужна и для номинальных данных. Такой характеристикой является мода. Она применяется как для неупорядоченных категорий, так и для упорядоченных, и для количественных данных.
Мода– это такое значение признака, которое встречается наиболее часто. В случае дискретных рядов вычислить моду нетрудно. Достаточно найти варианту, которая имеет наибольшую частоту или относительную частоту, это и будет мода. Будем обозначать моду символом Мо.
Если все значения в вариационном ряде встречаются одинаково часто, то считают, что этот ряд не имеет моды.
Если два соседних значения вариационного ряда имеют одинаковую частоту, и она больше частоты любого другого значения, то считают, что мода равняется среднему арифметическому этих значений.
Если два не соседних значения вариационного ряда имеют одинаковую частоту, и она больше частоты любого другого значения, то считают, что вариационный ряд имеет две моды, а соответствующее распределение называют бимодальным.
Пример использования моды в медицинских исследованиях:требуется определить среднюю длительность госпитализации рабочих промышленных предприятий в связи с производственным травматизмом.
| Число дней госпитализации | Итого | ||||||||
| Число рабочих |
При визуальном анализе графического изображения распределения видно, что ряд распределения несимметричен: вершина распределения сдвинута в начало ряда. Если определять среднюю величину на основе среднего арифметического (М), то средняя длительность одной госпитализации составит 4,2 дня. Однако, чаще всего (Мо) длительность госпитализации составляла 3 дня.
Для правильного выбора пути статистического анализа необходимо знать вид распределения изучаемого признака.
Под видом распределенияслучайной величины понимают соответствие, устанавливаемое между всеми возможными числовыми значениями случайной величины и вероятностями их появления в совокупности. Вид (закон) распределения может быть представлен:
- аналитической зависимостью в виде формулы;
- в виде графического изображения;
- в виде таблицы.
Виды распределений
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход и т.п., а потом построить график любой из этих величин, то получится функция распределения данной величины. В зависимости от исследуемого признака получаемые графики могут быть различны.
Посмотрим, как можно построить такой график на примере данных роста. Сначала, просто запишем результаты исследования. Потом, отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, "от 180 до 181 включительно". После этого необходимо посчитать количество людей в каждой подгруппе (диапазоне) –это будет частота попадания роста жителей города в данный диапазон. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить гистограмму – упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а высота будет равна той частоте, которая соответствует каждому диапазону роста. Если зарегистрированных данных было достаточно много, то полученный график будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения:
Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие.
Выделяют большое количество видов распределения признака в статистической совокупности. Остановимся на их краткой характеристике:
1) нормальное распределение
2) асимметричное распределение
- правостороннее
- левостороннее
- бимодальное
3) альтернативное распределение
Нормальное (Гауссово, симметричное, колоколообразное) распределение– одно из самых важных распределений в статистике. Оно характеризуется тем, что наибольшее число наблюдений имеет значение, близкое к среднему, и чем больше значения отличаются от среднего, тем меньше таких наблюдений. Примерами характеристик, подчиняющихся нормальному распределению, являются показатели роста, веса, какие-либо биохимические показатели крови.
Гауссово распределение характеризует распределение непрерывных