СЛУЧАЙ 1. Выборки независимые.
В этом случае нулевая гипотеза Н(0) звучит так:
• две генеральные средние равны
• или - две выборки извлечены из одной генеральной совокупности
• или - две совокупности имеют одинаковое распределение
В медицинских задачах гипотеза может быть сформулирована, например, таким образом: содержание гемоглобина у городских и сельских жителей одинаково (подразумевая, что одинаково его распределение).
Проверяемый t-критерий вычисляется по формуле
 (11)
(11)
где  – выборочные средние
– выборочные средние
m1, m2 - стандартные ошибки средних значений сравниваемых выборок.
Находим по таблице tкрит для заданного α и числа степеней свободы
f =n1 + n2 – 2 (12)
Если │tвыч │<tкрит то принимается Н(0) (нет аргументов, чтобы ее отвергнуть)
Если │tвыч│≥tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости.
Условие равенства двух генеральных дисперсий проверяется по критерию Фишера, который равен отношению большей выборочной дисперсии к меньшей:
 (13)
(13)
Fкрит находится по таблице (Приложение 7) для заданного αи числа степеней свободы
f1=n1-1 и f2=n2-1 (14)
Если Fвыч≥ Fкрит , то гипотеза о равенстве генеральных дисперсий отвергается
Если Fвыч< Fкрит , то принимается нулевая гипотеза о равенстве.
Пример. По данным из таблицы 14 определить, отличается ли при себорее содержание связанного холестерина крови (мг%) от нормы, если известно, что концентрация холестерина имеет нормальное распределение, а дисперсии в двух совокупностях одинаковы. Таблица 14. Данные к примеру
Решение: Вычислим средние значения для двух выборок:
Несмотря на то, что две выборочные средние отличаются, не исключена возможность, что генеральные средние равны. Поэтому выдвинем гипотезы: Н(0): среднее значение связанного холестерина в крови при себорее не отличается от нормы Н(1): среднее значение связанного холестерина в крови при себорее отличается от нормы Гипотезы будем проверять на уровне значимости α=0,05. Результаты вычислений представлены в таблице 15. Таблица15. Итоги проверки гипотезы
Определим Fкрит по таблице (Приложение 7) для f1=8 и f2=7 Fкрит=3,73 Т.к. Fвыч< Fкрит (1,08<3,73) принимаем гипотезу о равенстве генеральных дисперсий Определим tкрит для α=0,05 и числа степеней свободы в двух группах f=n1+n2-2=9+8-2=15 Из таблицы (Приложение 2) получаем двусторонний tкрит=2,13 т.к.│tвыч│> tкрит (20,8>2,13) – то принимается альтернативная гипотеза. Вывод: Содержание связанного холестерина в крови при себорреи статистически значимо отличается от нормы с вероятностью не менее 95%. |



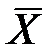 (мг%)
(мг%)