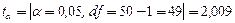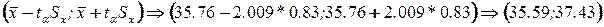Ден 10 дейінгі сандардың ондық логарифмдері

п
lgп		0,30	0,48	0,60	0,70	0,78	0,85	0,90	0,95

Бас орта

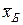бас орта деп бас жиынтық белгісінің орта арифметикалық мәнін айтады.

Егер N көлемді бас жиынтық белгісінің барлық х₁,......х_N мәндері әртүрлі болса, онда

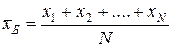
Егер x₁, x₂,….x_к белгісінің мәндері сәйкесінше N₁, N₂, …….N_k жиіліктерге ие болса,

мұнда N₁+ N₂+....+.N_k=N

;

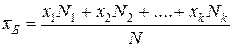Таңдама орта

Х сандық белгісіне қатысты бас жиынтықты зерттеу үшін n көлемді таңдама алынсын.

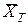таңдама орта деп таңдама жиынтық белгісінің орта арифметикалық мәнін айтады.

Егер n көлемді таңдаманың барлық x₁, x₂,….x_n мәндері әр түрлі болса, онда

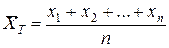
Егер таңдаманың x₁, x₂,….x_к мәндерінің сәйкесінше жиіліктері n₁, n₂,……..n_k болса, және

n₁+ n₂+…..+n_k = n онда

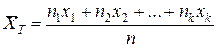
немесе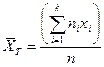

Көлемі n – ге тең Х сандық белгінің мәндер жиынтығын қарастырамыз.

Белгінің мәні	х1	х2	…	хк
Жиілік	п1	n2	…	пк

мұнда .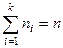

Жазуға қолайлы болу үшін 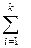қосынды таңбасы 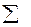таңбасымен ауысады.

Бас дисперсия

Бас жиынтықтың Х сандық белгісі мәндерінің өз орта мәнінің маңайында шашырауын сипаттау үшін бас дисперсия сипаттамасы енгізіледі.

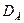бас дисперсиясы деп бас жиынтық белгісі мәндерінің 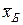орта мәнінен ауытқуының квадратының орта арифметикалық мәнін айтады.

Егер N көлемді бас жиынтық белгісінің барлық х₁, х₂ ,.., х_N мәндері әртүрлі болса, онда

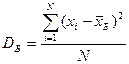
Егер белгінің барлық х₁, х₂ ,.., х_к мәндерінің сәйкес жиіліктері N₁, N₂, …, N_k бар болса, жәнеN₁+N₂+ +…+N_k=N, онда

;

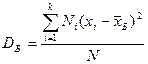Бас жиынтықтың сандық белгісі мәндерінің өз орта мәнінің маңайында шашырауын сипаттау үшін дисперсиядан басқа орта квадраттық ауытқуды пайдаланады.

Бас орташа квадраттық ауытқу деп бас дисперсиядан алынған квадрат түбірді айтады: .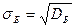

Таңдама дисперсия D_т деп белгінің бақыланатын мәндерінің 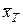орта мәнінен ауытқу квадраттарының орта арифметикалық мәнін айтады.

Егер n көлемді таңдаманың барлық x₁, x₂,….x_n белгілерінің мәндері әр түрлі болса, онда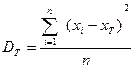

Егер x₁, x₂,….x_n мәндерінің жиіліктері бар және сәйкесінше n₁, n₂, …, n_k болса, мұндағы

n₁+ n₂+ …+ n_k=n, онда .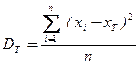

Теорема: Дисперсия таңдама мәндерінің квадраттарының орта мәні мен орта мәнінің квадратының айырымына тең: .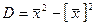

СЕНІМДІЛІК ИНТЕРВАЛЫ

Белгілі нүктелік таңдама сипаттамалар бойынша интервалды баға немесе сенімділік интервалын құруға болады, онда қандай да бір ықтималдықпен генеральды паратер орналасады. Белгілі таңдама көрсеткіштер негізіндегі генеральды параметрлер туралы сенімді түрде айтуға келетін болып есептелген ықтималдықтар сенімді деп аталады. Әдетте медициналық-биологиялық зерттеулерде Р=0,95 (95%) сенімділік ықтималдығының мәні қолданылады. Және де параметрдің нақты мәнінің осы шектерден шығу ықтималдығы 1–0,95=0,05 (5%)-тен аспайды. Сенімділік ықтималдықты толықтыратын шаманы әдетте α деп белгілейді.

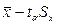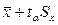Орталық шекті теоремадан білетініміздей, таңдамалар алынған бастапқы жиынтықтың тарамдалуына тәуелсіз таңдама орташалар жуықтап алғанда қалыпты тарамдалуға ие. Осылайша, таңдама орташа мән үшін сенімділік интервалы және мәндерінің арасында орналасқан, мұндағы S_x орташаның стандартты қатесі, t_α – Стьюдент коэффициенті, п таңдама көлеміне тәуелді (немесе сәйкес df=n-1 бостандық дәрежелірінің саны) шама және сенімділік ықтималдығының таңдалған деңгейіне тәуелді шама Стьюдент тарамдалу кестелері бойынша анықталады. t_α коэффициент шамасы сенімділік ықтималдығын 1-ге дейін толықтыратын α деңгейінде кесте бойынша анықталады, яғни сенімділік ықтималдығы 95% жағдайда интервал симметриясы ескерілгенде (1-0,95)=0,05 деңгейінде.

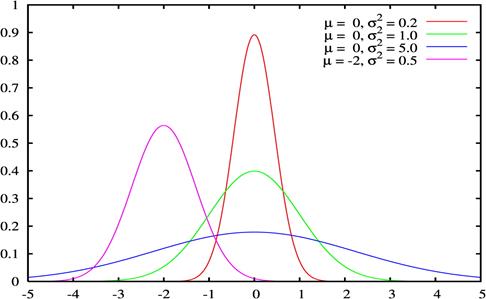
Қалыпты таралудың негізгі сипаттамалары:

Ø Сандық сипаттамалардың теңдігі (орта мән, мода және медиана өз ара тең);

Ø орта мәннен ауытқудың симметриялылығы;

Ø қисық астындағы жалпы аудан 1 ге тең;

Ø қисықтың ұштары екі бағытта да абцисса осіне үздіксіз жақындай отырып, алайда ешқашан онымен жанаспай шексіздікке ұмтылады.

Ø қисықтың түрі бас жиынтықтың орта квадраттық ауытқуымен анықталады;

Ø орта квадраттық ауытқуы аз таралуға жіңішке, жоғары созылған қисықтар, ал орта квадраттық ауытқуы үлкен таралуға жазыңқы қисықтар сәйкес келеді.

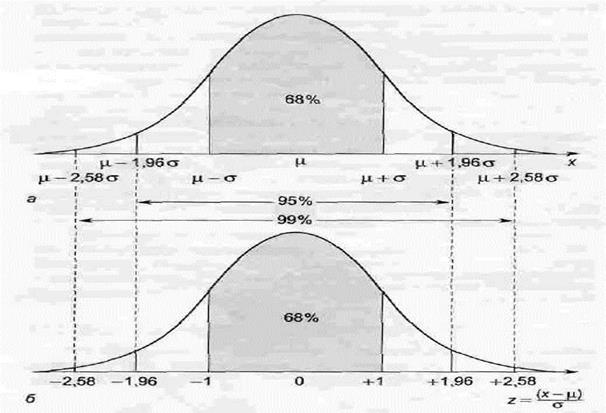
3 сигма ережесі.

барлық мәндердің 68,26% -і ±σ аралығында жатады (орта мәннен ±1 орта квадраттық ауытқу);

барлық мәндердің 95,44% -і 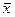±2σ аралығында жатады ( орта мәннен ±2 орта квадраттық ауытқулар);

барлық мәндердің 99,73% -і 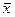±3σ аралығында жатады (орта мәннен ±3 орта квадраттық ауытқулар).

Гаусс қисығы

Қалыпты таралу тығыздығының графигін қалыпты қисық немесе Гаусс қисығы деп атайды.

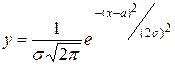
Қалыпты таралудың қисығы центрге қатысты симметриялы, қоңырау тәрізді түрі бар

Сигма ережесі.

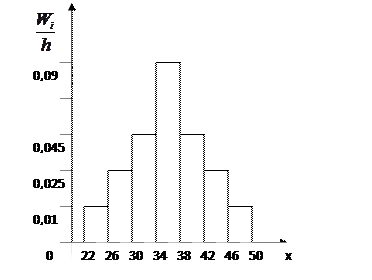
Мысал. Өте үлкен ампулалар партиясынан көлемі 50 болатын кездейсоқ таңдама алынды. Х белгісі – 1 см-ге дейінгі дәлдікпен өлшенген ампулалардың ұзындығы келесі вариациялық қатар түрінде берілген: 22, 24, 26, 26, 27, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Таралудың статистикалық дискретті, интервалдық қатарларын, мода, медиана, таңдама ортасын, дисперсияны, орта квадраттық ауытқу, сенімділік интервалын табу керек және тең қадаммен жиілік және салыстырмалы жиілік гистограммасын тұрғызу керек. Таңдаманың қалыпты таралу заңына бағынатындығын немесе бағынбайтындығын тексеру керек (3 сигма ережесінің орындалуы).

Шешімі. Таңдаманың дискретті статистикалық таралуы

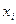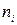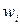	0,02	0,02	0,04	0,02	0,04	0,06	0,04	0,08	0,1	0,04	0,1	0,12	0,04	0,1	0,04	0,02	0,04	0,04	0,02	0,02

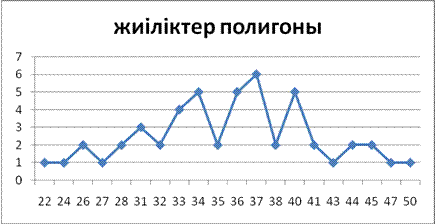
Мода М₀=37.

Медиана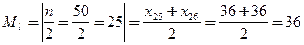

Таңдама орта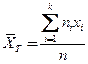

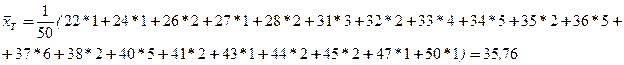
Таңдама дисперсия

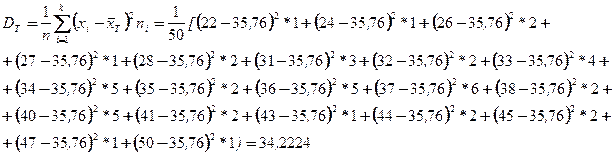
Таңдама орта квадраттық ауытқу деп таңдама дисперсиядан алынған квадрат түбірді айтады: .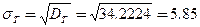

Таңдама ортаның стандартты қатесі:

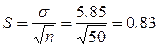
Бас орта 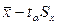және 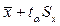сенім интервалының арасында жатады.