Пример построения вариационных рядов, вычисления средних величин, создания графика распределения признака и проверки на нормальность распределения.
Условие задачи: Для выявления общей характеристики частоты сердечных сокращений (ЧСС) детей 1-го года жизни в отделении №1 больницы выполнено 16 измерений пульса у детей:
1. Иванов Василий – 120 уд.в мин.
2. Сидоров Костя – 130 – “ -
3. . . . - 115
4. . . . - 120
5. . . . - 120
6. . . . - 125
7. . . . - 110
8. . . . - 125
9. . . . - 115
10. . . . - 120
11. . . . - 125
12. . . . - 135
13. . . . - 115
14. . . . - 130
15. . . . - 125
16. . . . - 120
Задание: а) составить простой вариационный ряд;
б) вычислить простую среднюю арифметическую вариационного ряда;
в) определить степень рассеяния вариант в вариационном ряду;
г) выполнить группировку и упорядочение (ранжирование) ряда по возрастанию и построить график распределения признака;
д) определить медиану;
е) определить моду и среднюю взвешенную величину;
ж) определить статистические критерии нормальности распределения;
з) определить доверительные границы колебания средней арифметической в генеральной совокупности.
Решение: запустите программу Excel, откройте файл в папке своей учебной группы под именем «Статистика–Фамилии студентов». Создайте НОВЫЙ лист, переименуйте его, обозначив названием «Сред_вел». На этом листе введите данные и решение задачи, как показано ниже, сохраните изменения и покажите результат работы преподавателю.
а) построение простого вариационного ряда частоты пульса детей, поступивших в отделение №1 больницы. Простой вариационный ряд представляет собой статистическую таблицу, в которой подлежащим является изучаемый признак, обозначаемый знаком V (варианта). Полученные в эксперименте данные вносят в таблицу в порядке их записи в журнал регистрации (условия задачи). Затем вычисляют сумму вариант, среднюю арифметическую, отклонения (d) каждой варианты от средней величины и квадрат отклонения (d2) соответствующими формулами (таблица 15).
Таблица 15
Простой неранжированный вариационный ряд
| V | d=V-M | d2 | |
| 1 Иванов Василий | -1,88 | 3,52 | |
| 2 Сидоров Костя | 8,13 | 66,02 | |
| 3 … | -6,88 | 47,27 | |
| 4 … | -1,88 | 3,52 | |
| 5 … | -1,88 | 3,52 | |
| 6 … | 3,13 | 9,77 | |
| 7 … | -11,88 | 141,02 | |
| 8 … | 3,13 | 9,77 | |
| 9 … | -6,88 | 47,27 | |
| 10 … | -1,88 | 3,52 | |
| 11 … | 3,13 | 9,77 | |
| 12 … | 13,13 | 172,27 | |
| 13 … | -6,88 | 47,27 | |
| 14 … | 8,13 | 66,02 | |
| 15 … | 3,13 | 9,77 | |
| 16 … | -1,88 | 3,52 | |
| Сумма S) = | 1950 | 0,00 | 643,75 |
| n=16 |
б) вычисление средней арифметической (M) в простом вариационном ряду выполняется по формуле:
= 1950/16 = 121,9 уд/мин.
В программе Excel для вычисления средней арифметической может применяться функция =СРЗНАЧ(Диапазон ячеек). Использование этой функции даст такой же результат.
в) вычисление среднего квадратического отклонения (σ- Сигма), ошибки средней (m, ошибка репрезентативности или стандартная ошибка) и коэффициента вариации (С):
= КОРЕНЬ(643,75 / 16) = 6,343.
Для упрощения расчета среднего квадратического отклонения при n > 30 может использоваться формула вычисления стандартного отклонения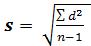 
, которая в знаменателе содержит -1. В программе Excel стандартное отклонение вычисляется функцией =СТАНДОТКЛОН(Диапазон данных).
=6,343 / КОРЕНЬ(16-1) = 1,64
= 6,343/121,9 * 100 = 5,2% - малое рассеяние (<10%).
Вариабельность признака (рассеяние) оценивается как малая при С<10%, средняя при 10%< С < 20%, высокая при С >20%