Доверительные интервалы для показателей точности и информативности при формировании общепопуляционной выборки
При формировании выборки по схеме общепопуляционного скринингового исследования основные показатели точности – чувствительность (Se), специфичность (Sp),и показатели информативности – предсказательные ценности позитивов (PPV) и негативов (NPV) и распространенность заболевания (Prev) являются простыми долями. Поэтому для их интервальных оценок используются известные методы построения 100(1 – α)%-го ДИ для параметра биномиального распределения.
В общем виде, если оцениваемый параметр φ = P(A) есть неизвестная вероятность события A, которую нужно оценить, то ее точечной статистической оценкой является соответствующая частота
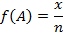
Где x – число испытаний с исходами A, а n – общее число исходов.
Для нахождения границ 100(1 – α)%-го ДИ для оцениваемого параметра можно использовать точный метод Клоппера-Пирсона.
Нижняя граница вычисляется по формуле:
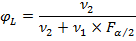
Здесь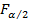 
– такое значение функции F-распределения Снедекора-Фишера при числах степеней свободы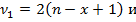 
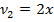, что 
.
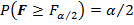Верхняя граница вычисляется по формуле:
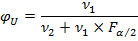
А здесь 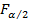– такое значение функции F-распределения Снедекора-Фишера при числах степеней свободы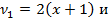 
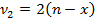, что .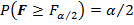
См., например:
Глотов Н.В., Животовский Л.А., Хованов Н.В., Хромов-Борисов Н.Н. Биометрия: Учеб. пособие. – Л.: Изд-во Ленингр. Ун-та, 1982. – 263 с.
Доверительные интервалы для PPV и NPV при формировании выборок по схеме «случаи-контроли»
При формировании двух независимых выборок по схеме «случаи-контроли» для построения доверительных интервалов для предсказательных вероятностей PPV и NPV нужны «внешние данные» данные о распространенности диагностируемого заболевания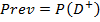 
:
Для удобства упростим нашу символику и введем следующие обозначения:
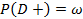- распространенность болезни
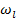- нижнее из известных значений для распространенности (нижняя граница для размаха распространенности)
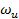- верхнее из известных значений для распространенности (верхняя граница для размаха распространенности)
Соответственно, формула для точечной статистической оценки PPV принимает вид:
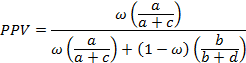
Введем «промежуточный» параметр η
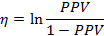
Его дисперсию можно оценить как
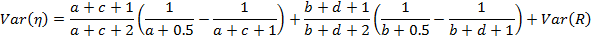
где
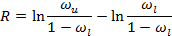
а дисперсию R, в свою очередь, можно оценить как
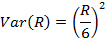
Тогда статистической оценкой нижней границы 100(1 – α)%-го ДИ для η будет:
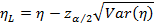
а оценкой его верхней границы будет:
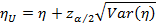
В итоге получаем следующие статистические оценки границ 100(1 – α)%-го ДИ для PPV:
нижняя
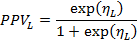
и верхняя
Аналогичным образом находим статистические оценки границ ДИ для NPV. В этом случае приведенных формулах вместо PPV подставляем NPV и вместо данных о распространенности используем ее дополнение
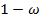
Источник:
Zaykin D.V., Meng Z., Ghosh S.K. Interval estimation of genetic susceptibility for retrospective case-control studies // BMC Genetics, 2004. – V. 5. – paper 9.
URL: http://www.biomedcentral.com/content/pdf/1471-2156-5-9.pdf
Доверительные интервалы для LR[+] и LR[-]
Вычисляем стандартные ошибки (SE) для логарифма LR на основе статистики PRAC2
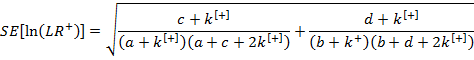
где
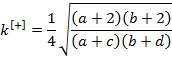
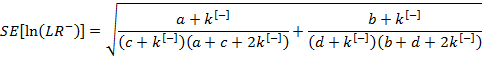
где
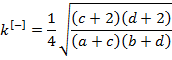
ДИ для LR[+]
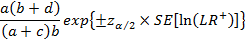
ДИ для LR[-]
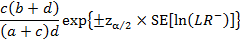
Источник:
Bolboacă S., Jäntschi L. Binomial distribution sample confidence interval estimation for positive and negative likelihood ratio medical key parameters // AMIA Annu. Symp. Proc., 2005. – P. 66-70. [American Informatics Medical Association, Bethesda, Special Issue: from Foundation to Application Policy (Proc. CD, October 22-26, Washington D.C., USA), 2005. – P. 66-70].
URL: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1560461/