Достоверность разности между двумя сравниваемыми величинами

При оценке достоверности разности результатов исследования в двух группах нередко

приходится решать вопрос, является ли это различие существенным, обусловленным действием

разных факторов (например, методов лечения, вакцинации и т.д.) или вызвано случайными

колебаниями.

Достоверность разностимежду двумя относительными величинами определяются по форму

ле: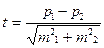

где Р₁ иР₂ - показатели, полученные при выборочных исследованиях m₁ и m₂ -соответствующие

ошибки.

Оценка достоверности разности средних арифметических проводится по

формуле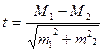, где M₁ и M₂ - сравниваемые средние величины; m₁ и m₂ - ошибки

сравниваемых средних величин.

Полученный критерий t оценивается по общепринятым правилам: если t³ 2, то различие

показателей следует считать достоверным, т.е. оно соответствует вероятности безошибочного

прогноза, равной 95% (Р <0,05)

Пример: Сравнение результатов лечения пенициллином и тетрациклином больных рожистым

воспалением.

Виды антибиотиков	Число наблюдаемых больных	Имели рецидивы
		абс. число	%
Пенициллин			15,0
Тетрациклин			7,6

Разность показателей = Р₁ - Р₂ = 15% - 7,6% = 7,4%. Действительно ли тетрациклин более

эффективен при рожистым воспалении? Можно ли быть уверенным в том, что при применении

этих антибиотиков и большой группы больных тетрациклин будет давать лучшие результаты,

чем пенициллин?

Достоверность выводов необходимо обосновать статистическим расчетом. Для этого:

1) Вычислить среднюю ошибку (m) для каждого показателя:

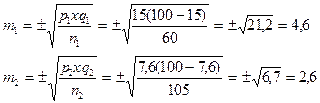
2) Оценить достоверность различий частоты рецидивов заболеваний в двух группах:

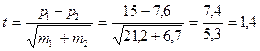
Разность между показателями (7,4) превышает ошибку (5,3) меньше чем в 2 раза, что не

позволяет признать различие показателей достоверным. Поэтому большую эффективность

тетрациклина по сравнению с пенициллином при лечении рожистого воспаления нельзя

считать доказанной.

В медицинской литературе чаще вероятность достоверности выражается не критерием t, а

уровнем значимости (P) , который является дополнением доверительной вероятности до 100%

(или до 1,0). Так вероятности 95% (0,95) соответствует уровень значимости 0,05 (1,0 - 0,95 =

0,05), вероятности 99% - 0,01 (1 - 0,99=0,01), вероятности 99,9% - 0,001 (1 - 0,999=0,001).

Стандартные значения критерия Стьюдента (t_st)

V	t1	t2	t3	V	t1	t2	t3
n	0,05	0,01	0,001	n	0,05	0,01	0,001
	12,71	63,66	637,0		2,08	2,83	3,82
	4,30	9,93	31,60		2,07	2,82	3,79
	3,18	5,84	12,94		2,07	2,81	3,77
	2,78	4,60	8,61		2,06	2,80	3,75
	2,57	4,03	6,86		2,06	2,79	3,73
	2,45	3,71	5,96		2,06	2,78	3,71
	2,36	3,50	5,41		2,05	2,77	3,69
	2,31	3,36	5,04		2,05	2,76	3,67
	2,26	3,25	4,78		2,04	2,76	3,66
	2,23	3,17	4,59		2,04	2,75	3,65
	2,20	3,11	4,44		2,02	2,70	3,55
	2,18	3,06	4,32		2,01	2,68	3,50
	2,16	3,01	4,22		2,00	2,66	3,46
	2,15	2,98	4,14		1,99	2,64	3,42
	2,13	2,95	4,07		1,98	2,63	3,39
	2,12	2,92	4,02		1,98	2,62	3,37
	2,11	2,90	3,97		1,97	2,60	3,34
	2,10	2,88	3,92		1,96	2,59	3,31
	1,96	2,86	3,88	¥	1,96	2,58	3,29
	2,09	2,85	3,85
	5%	1%	0,1%		5%	1%	0,1%