Его формула, график, особенности
ЯГМА
Медицинская физика
Лечебный факультет
Курс
Семестр
Поток
Лекция № 2
«Элементы математической статистики»
Составил: Бабенко Н.И.
Г.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ,
ЕГО ФОРМУЛА, ГРАФИК, ОСОБЕННОСТИ.
Нормальное распределение ( по имени авторов - распределение Гаусса-Лапласа ) названо так потому, что оно наиболее часто встречается на практике, и прежде предполагалось, что такое распределение является «нормой» для всех массовых явлений.
Для медицинской практики наиболее важными являются следующие виды нормального распределения:
ü эмпирическое нормальное распределение;
ü общее ( теоретическое ) нормальное распределение;
ü стандартное нормальное распределение.
Эмпирическое нормальное распределение - это распределение, полученное опытным путем на основе статистического исследования.
Особенность этого распределения в том, что объем его совокупности всегда конечен.
Общее ( теоретическое ) нормальное распределение - это абстрактная математическая модель, которую используют в качестве стандарта для сравнения с эмпирическим ( опытным ) распределением по разным статистическим критериям.
Особенность этого распределения в том, что оно построено в предложении, что объем совокупности является бесконечно большим.
Общее нормальное распределение описывается формулой: 
Здесь y=f(x) - функция, равная частоте встречаемости вариантов с данным значением признака;
N - объем совокупности;
е и π - математические постоянные, равные 2,71 и 3,14 соответственно;
σ, s – стандартные отклонения ( генеральное - σ, выборочное – s );
t - показатель, который называется «нормированное отклонение» и вычисляется по формуле 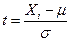 , где
, где
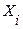 - числовое значение конкретной варианты,
- числовое значение конкретной варианты,
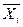 или μ - средняя арифметическая выборочной или генеральной совокупности.
или μ - средняя арифметическая выборочной или генеральной совокупности.
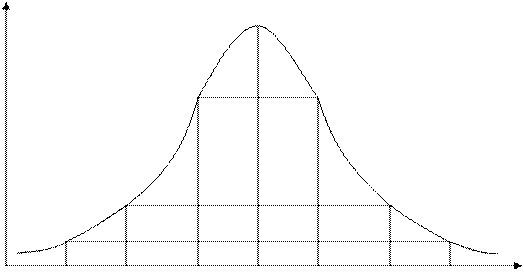
График общего ( теоретического ) нормального распределения представляет собой унимодальную ( одновершинную ) симметричную вариационную кривую.
Эту кривую строят в прямоугольной системе координат, где по горизонтали откладывается текущее числовое значение признака xi в порядке возрастания, а по вертикали - значение функции y = f(x), которое соответствует числу объектов ( вариантов) с данным числовым значением признака.
График нормального распределения
 Y
Y  =Mo=Me
=Mo=Me
σ
2σ
3σ
 X
X
Особенности нормального распределения:
1. Кривая распределения симметрична относительно средней арифметической (  илиμ ).
илиμ ).
2. Чем больше отклоняются числовые значения вариантов от средней арифметической, тем реже такие варианты встречаются в совокупности.
3. Площадь под кривой равна объему совокупности N.
4. В пределах площади, отсекаемой перпендикулярами к горизонтали в точках:
/ 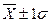 / находится 68.3% всех наблюдений,
/ находится 68.3% всех наблюдений,
/ 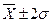 / находится 95.5% всех наблюдений,
/ находится 95.5% всех наблюдений,
/ 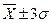 / находится 99.7% всех наблюдений,
/ находится 99.7% всех наблюдений,
/ 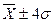 / находится 99.93% всех наблюдений.
/ находится 99.93% всех наблюдений.
5. Для общего ( теоретического ) нормального распределения средняя арифметическая  , мода Moи медиана Me равны между собой:
, мода Moи медиана Me равны между собой:
 =Mo=Me.
=Mo=Me.
6. Смещение кривой по горизонтальной оси определяется числовым значением средней арифметической.
7. Степень вытянутости кривой по вертикали зависит от значения стандартного отклонения. Чем меньше числовое значение имеет стандартное отклонение σ, тем более острой будет кривая.
8. Наибольшее значение функции y имеет тогда, когда числовое значение конкретной варианты равно значению средней арифметической xi =  . При этом величина максимума будет равна
. При этом величина максимума будет равна 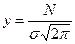 .
.
