Линейное напряженное состояние
Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис.3.6).
Примером линейного напряженного состояния может служить осевое растяжение-сжатие.
Рассмотрим задачу определения напряжений в площадке общего положения. Угол наклона этой площадки α будем отмерять от направления 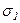 до нормали к площадке
до нормали к площадке 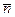 . Примем, что положительный угол α откладывается против хода часовой стрелки, а отрицательный по ходу часовой стрелки. Направим ось х вдоль нормали
. Примем, что положительный угол α откладывается против хода часовой стрелки, а отрицательный по ходу часовой стрелки. Направим ось х вдоль нормали 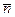 , ось у – перпендикулярно ей
, ось у – перпендикулярно ей
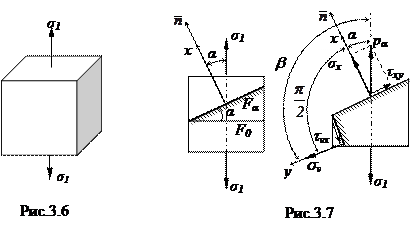
Для определения напряжений s x и t ху рассмотрим рис.3.7.
Получим:
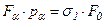
где 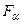 - площадь наклонной площадки,
- площадь наклонной площадки,
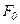 - площадь поперечного сечения,
- площадь поперечного сечения,
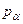 - полное напряжение, действующее по наклонной площадке.
- полное напряжение, действующее по наклонной площадке.
Учитывая, что 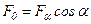 , получим:
, получим:
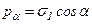 .
.
Раскладывая pa на направление оси х и оси у, получим
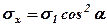 ,
,
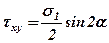
Рассмотрим площадку b перпендикулярную площадке a, угол
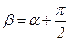 . Направим ось y по нормали к этой площадке. Нормальные напряжения, действующие по этой площадке равны
. Направим ось y по нормали к этой площадке. Нормальные напряжения, действующие по этой площадке равны
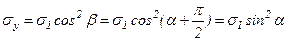 .
.
Складывая sх и sу , получим
sx + sy = s1 = const,
т.е.сумма нормальных напряжений по двум взаимно перпендикулярным площадкам величина постоянная и равна главному напряжению.
Касательные напряжения, действующие по наклонной площадке b
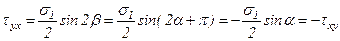 ,
,
т.е. справедлив закон парности касательных напряжений.
Нормальные напряжения sx по наклонной площадке a достигают максимального значения 
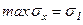 при a = 0, т.е. в поперечном сечении.
при a = 0, т.е. в поперечном сечении.
Касательные напряжения τxy по наклонной площадке a достигают максимального значения 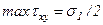 при a = ± 450.
при a = ± 450.
Плоское напряженное состояние
Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.
На рис.3.8 показано плоское напряженное состояние.
Прямая задача.
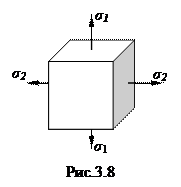 Определим напряжения sx и txy, действующие по любой наклонной площадке a по известным главным напряжениям
Определим напряжения sx и txy, действующие по любой наклонной площадке a по известным главным напряжениям 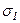 и
и 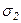 , т.е. решим так называемую прямую задачу теории напряженного состояния.
, т.е. решим так называемую прямую задачу теории напряженного состояния.
Для решения этой задачи воспользуемся принципом независимости действия сил.
Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений s1, второе – при действии только напряжений s2 (рис.3.9)
От каждого из напряжений s1, s2 напряжения sx1, sx2 и txy1,txy2 в произвольной площадке равны
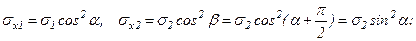
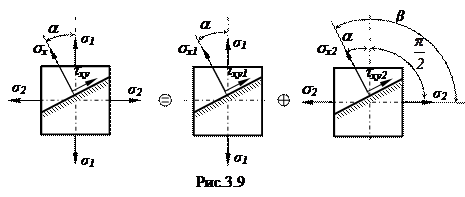
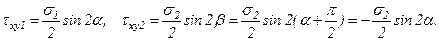
Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим
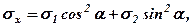
(3.1)
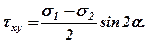
Если рассмотреть площадку с углом наклона 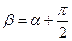 , перпендикулярную к площадке a, то можно доказать как и для линейного напряженного состояния, что
, перпендикулярную к площадке a, то можно доказать как и для линейного напряженного состояния, что
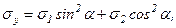
(3.2)
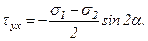
Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим
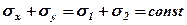 .
.
Сравнивая величины касательных напряжений, получим
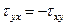 .
.
Наибольшие касательные напряжения действуют по площадкам, наклоненным к главным под углом a = 45о
