Понятия о перемещениях и деформациях

Под действием внешних сил любое тело деформируется, т.е. его форма и размеры изменяются, а точки тела меняют положение в пространстве. Пусть имеется тело с приложенными к нему силами Р_i. Мысленно через точку а в направлениях осей у и z проведем бесконечно малые отрезки ав и ас, длины которых dy и dz. После деформации бруса отрезки примут положение, изображенное штриховой линией (рис.1.13). Точка а переместится в положение а₁. Величина аа₁, равная изменению координат точки называется линейным перемещением точки а. Отрезки ав и ас займут новые положения а₁в₁ и а₁с₁. Их длины изменяются на Δdy и Δdz и называются абсолютными линейными деформациями. Угол между начальным положением отрезка ав и конечным - а₁в₁ - называются угловым перемещением b. Линейные перемещения измеряются в единицах длины, угловые - в радианах или градусах. Отношение приращения длины отрезка к его начальной длине представляет собой относительную линейную деформацию, т.е. 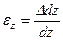. Аналогично 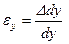. Линейные деформации величины безразмерные. Изменение первоначально угла между отрезками ав и ас после приложения к телу нагрузки, выраженное в радианах, представляет собой угловую деформацию .

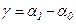Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.

1. Условие жёсткости.

Ответ:

Жёсткость – это способность тела или конструкции сопротивляться деформации.

1. Энергетическая теория прочности.

Ответ:

Четвертая теория прочности - энергетическая, представляет собой гипотезу о том, что причиной возникновения опасного состояния является величина удельной потенциальной энергии изменения формы 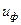, то есть критерий – удельная потенциальная энергия изменения формы.

Формулу удельной потенциальной энергии изменения формы получим из формулы полной удельной потенциальной энергии деформации (3.5), подставляя значение коэффициента Пуассона равного ν=0,5.

Получим

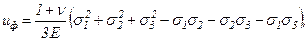
Условие прочности имеет вид

,

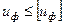где

.

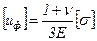Откуда

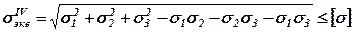
Третья и четвертая теории прочности дают удовлетворительное совпадение результатов теоретического расчета с опытными данными для пластичных материалов и широко применяются при расчетах на прочность. Для хрупких материалов эти теории не применимы.

Билет №10.

1. Виды простых деформаций стержня.

Ответ:

Растяжением или сжатием называют такой вид деформации бруса (стержня), при котором в его поперечных сечениях возникает только продольная сила N.

Продольная сила, направленная от сечения, связана с растяжением и считается положительной; сила, направленная к сечению; связана со сжатием и считается отрицательной.

При расчёте стержня на прочность необходимо знать значения внутренних силовых факторов во всех его сечениях. Для этого строят график (эпюру), показывающий, как изменяется внутренний силовой фактор (сила или момент) по длине стержня.

1. Статически неопределимые задачи при одноосном растяжении (сжатии).

Ответ:

Системы, для которых все реакции связей могут быть определены с помощью уравнений равновесия, называются статически определимыми.

Системы, для которых количество реакций связей превышает число возможных уравнений равновесия, называются статически неопределимыми системами.

Разность между числом неизвестных и числом независимых уравнений равновесия определяет степень статической неопределимости.

Дополнительные уравнения, называемые уравнениями совместности перемещений, составляют, определяя перемещения отдельных стержней системы и устанавливая между ними связь.

1. Теория прочности Мора.

Ответ:

Теория прочности Мора не содержит критериальных гипотез и основана в первую очередь на логической систематике экспериментальных результатов. Её основное допущение заключается в том, что главное напряжение 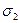не оказывает влияния на прочность. Для получения выражения для 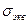строятся круги Мора для предельных напряжённых состояний, т.е. состояний, при которых начинается пластическое деформирование или разрушение. Круги для одноосного сжатия и одноосного растяжения строятся достаточно достоверно, т.к. одноосное растяжение и одноосное сжатие легко реализуется экспериментально. К этим кругам проводится общая касательная, которая в некотором приближении рассматривается как огибающая предельных кругов Мора(диаграмм для предельных напряжённых состояний). Предельные круги Мора для любого напряжённого состояния не должны выходить за огибающую. Опуская дальнейшие геометрические построения, дадим окончательный результат для эквивалентного напряжения:

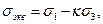(1)

где 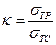- для пластичных материалов.

Для хрупких материалов отношение 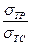заменяется на .

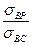Условие прочности запишется в виде:

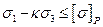(2).

Наилучшие результаты эта теория даёт для случая, когд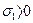а , а 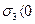. Это обстоятельство существенно, т.к. при решении практических задач напряжённое состояние такого рода встречается чаще других. Для многих пластичных материалов у которых 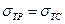теория прочности Мора совпадает с теорией максимальных касательных напряжений.

Билет №11.

1. Сложные виды деформации бруса.

Ответ:

. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми. Основные соотношения, полученные для них, приведены в таблице 7.1

Таблица 7.1

Виды нагружения	Напряжения	Деформации
Растяжение	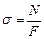. Условие прочности:
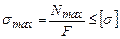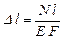Изгиб	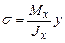. Условие прочности:
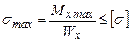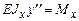Кручение	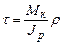. Условие прочности:

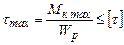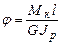Кроме простых видов нагружения бывают и сложные виды нагружения или иначе сложное сопротивление.

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:

* · косой изгиб;

* · внецентренное растяжение;

* · изгиб с кручением.

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.

1. Расчёты статически неопределимых стержневых систем на силовые, температурные и кинематические воздействия.

Ответ:

При эксплуатации конструкции возможно изменение температуры, вызванное условиями работы или сменой времен года. С изменением температуры изменяются линейные размеры элементов конструкции: увеличиваются при нагреве, уменьшаются при охлаждении на величину 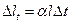, где 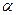- температурный коэффициент линейного расширения (для стали температурный коэффициент линейного расширения 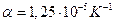); 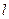- длина элемента; 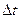- изменение температуры, К.

В статически определимых системах длина стержня может свободно изменяться при их нагреве или охлаждении.

В статически неопределимых системах при изменении температуры возникают дополнительные силы. Если нагреть стержень, жёстко закреплённый по концам, то его длина не может изменяться: этому препятствуют жёсткие заделки. В опорах (заделках) возникают реакции, сжимающие стержень.

1. Понятие о новых теориях прочности.

Ответ:

Критерии прочности и пластичности, рассмотренные в предыдущих параграфах, справедливы для традицион­ных конструкционных материалов — однородных и изо­тропных. Однако в последнее время в различных облас­тях техники, в том числе и в строительстве, все большее распространение получают новые, так называемые ком­позиционные материалы (композиты). Композит пред­ставляет собой полимерную или металлическую матри­цу, армированную высокопрочными волокнами (стеклян­ными, угольными и т. п.). Отличительными признаками этих материалов являются их неоднородность и, как правило, ярко выраженная анизотропия свойств. Послед­нее обстоятельство находит отражение, в том числе и в прочностных свойствах композитов.

Армирование композита может быть однонаправленным (рис. 14.9, а), ортогональным (рис. 14.9, б), симмет­ричным в нескольких направлениях (рис. 14.9, в).

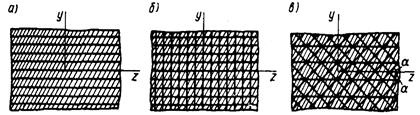
Рис. 14.9. Схемы армирования композитов

При однонаправленном армировании прочность ма­териала в направлении армирования высокая, а в ор­тогональном направлении значительно меньше, потому что определяется в основном прочностью матрицы.

Если подвергнуть однонаправленный композит испы­танию на растяжение или на сдвиг, то разрушение может произойти частично за счет разрыва волокон, а частично за счет скалывания матрицы. Аналогичные соображения оказываются справедливыми и в общем случае армиро­вания композиционных материалов волокнами.

Условие прочности композита можно записать в сле­дующем виде:

.

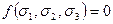В настоящее время известно большое число различ­ных критериев прочности, предложенных для новых кон­струкционных материалов. В частности, один из критери­ев прочности для ортотропных материалов представляет собой обобщение критерия текучести по удельной энер­гии формоизменения и в случае плоского напряженного состояния записывается следующим образом:

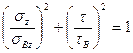, (14.9)

где 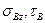— пределы прочности материала при растяже­нии — сжатии в направлении оси z (оси упругой симмет­рии, рис. 14.9, а, б) и при сдвиге; 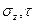— нормальное напряжение в направлении оси z и касательное напряже­ние.

Если материал имеет разные пределы прочности при растяжении и сжатии, то могут быть использованы усло­вия прочности вида

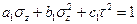, или .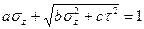

Константы, фигурирующие в этих соотношениях, определяются из опытов на растяжение, сжатие и сдвиг.

Следует обратить внимание на то, что результаты испытаний композитов обладают очень большим случай­ным разбросом и потому указанные константы должны находиться лишь на основе статистического анализа. По­следнее обстоятельство тем более затрудняет выбор на­илучшего критерия прочности композиционного матери­ала.

Среди композитов, применяемых в строительстве, на­ибольшее распространение имеют всевозможные поли­мерные материалы, на прочность которых оказывают большое влияние многие факторы, среди которых в пер­вую очередь нужно назвать температуру и время. Напри­мер, увеличение температуры всего на 20...30°C приводит к заметному снижению прочности указанных материа­лов. Еще более существенным при оценке прочности их является учет временного фактора. Обсуждению этого вопроса посвящена гл. 16.

Билет №12.

1. Виды пространственных деформаций стержня.

Ответ:

Под действием внешних сил любое тело деформируется, т.е. его форма и размеры изменяются, а точки тела меняют положение в пространстве. Пусть имеется тело с приложенными к нему силами Р_i. Мысленно через точку а в направлениях осей у и z проведем бесконечно малые отрезки ав и ас, длины которых dy и dz. После деформации бруса отрезки примут положение, изображенное штриховой линией (рис.1.13). Точка а переместится в положение а₁. Величина аа₁, равная изменению координат точки называется линейным перемещением точки а. Отрезки ав и ас займут новые положения а₁в₁ и а₁с₁. Их длины изменяются на Δdy и Δdz и называются абсолютными линейными деформациями. Угол между начальным положением отрезка ав и конечным - а₁в₁ - называются угловым перемещением b. Линейные перемещения измеряются в единицах длины, угловые - в радианах или градусах. Отношение приращения длины отрезка к его начальной длине представляет собой относительную линейную деформацию, т.е. 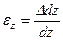. Аналогично 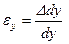. Линейные деформации величины безразмерные. Изменение первоначально угла между отрезками ав и ас после приложения к телу нагрузки, выраженное в радианах, представляет собой угловую деформацию .

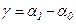Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.

1. Свойства статически неопределимых стержневых систем.

Ответ:

Разность между числом неизвестных и числом независимых уравнений равновесия определяет степень статической неопределимости.

Системы, для которых количество реакций связей превышает число возможных уравнений равновесия, называются статически неопределимыми системами.

1. Классификация видов изгиба. Изгиб балки в главной плоскости инерции.

Ответ:

Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты.

Изгиб называется плоским, если плоскость действия момента проходит через главную центральную ось инерции сечения.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы 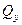изгиб называется поперечным.

Брус, работающий при изгибе, называется балкой.

Билет №13.

1. Главный вектор и главный момент внутренних усилий. Понятие о внутренних силовых факторах.

Ответ:

Внутри любого материала имеются внутренние межатомные силы. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) их, т.е. появление дополнительных внутренних сил. Дополнительные силы взаимодействия, возникающие внутри объекта под действием внешних сил, называются в сопротивлении материалов внутренними силами.

Для определения внутренних усилий используется метод сечений.

Существует шесть составляющих, которые называются внутренними силовыми факторами (В.С.Ф):

N - продольная (нормальная) сила, проекция вектора R на ось z;

Q_x, Q_y - поперечные силы, проекции вектора R на оси x, y соответственно;

M_z=M_к - крутящий момент, составляющая момента M вокруг оси z;

M_x, M_y - изгибающие моменты, составляющие момента M вокруг осей x, y соответственно.

1. Напряжения при чистом сдвиге. Соотношение упругости. Модуль упругости второго рода (модуль сдвига).

Ответ:

Чистый сдвиг

Пусть по граням параллелепипеда действуют главные напряжения 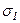=s, 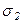= - s , (рис.3.10).

Определим величины нормальных и касательных напряжений, действующих в площадках повернутых под углом 45^о к главным. Из формул (3.1) получим, что

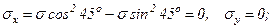
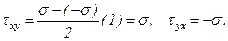
Напряженное состояние, при котором по граням выделенного элемента действуют только касательные напряжения, называется чистым сдвигом, а площадки - площадками чистого сдвига.

Экспериментально установлено, что существует линейная зависимость между углом сдвига g и касательными напряжениями t (рис.3.11), являющейся законом Гука при сдвиге

,

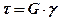где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.

Величина модуля сдвига связана с модулем упругости при растяжении Е и коэффициентом Пуассона ν соотношением

Упругостью называется свойство тел восстанавливать свои первоначальные форму и размеры после снятия нагрузки.

В пределах малых удлинений для большинства материалов справедлив закон Гука - нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации e

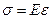. (2.2)

Коэффициент пропорциональности E - модуль продольной упругости, его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.

1. Внутренние силовые факторы и нагрузки.

Ответ:

Существует шесть составляющих, которые называются внутренними силовыми факторами (В.С.Ф):

N - продольная (нормальная) сила, проекция вектора R на ось z;

Q_x, Q_y - поперечные силы, проекции вектора R на оси x, y соответственно;

M_z=M_к - крутящий момент, составляющая момента M вокруг оси z;

M_x, M_y - изгибающие моменты, составляющие момента M вокруг осей x, y соответственно.

По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. Динамические нагрузки (переменные) - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию (например, ударные).

Билет №14.

1. Напряжения в сечении бруса. Понятие о полном, нормальном и касательном напряжении.

Ответ:

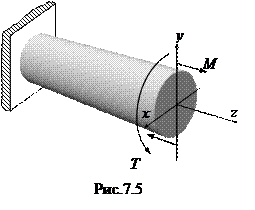При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала

.

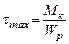При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах

.

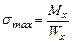1. Расчёт заклёпочных соединений.

Ответ:

Рассмотрим основы практических расчетов на срез заклепочных соединений. Более подробно эти вопросы освещаются в курсах деталей машин и конструкций. На рис. 5.5 показано соединение двух листов заклепками (соединение внахлестку). Соединение разрушается в результате перерезывания заклепок по линии соприкосновения листов. Если разрушение каждой заклепки происходит по одной плоскости среза, то заклепочное соединение называется односрезным, если по двум плоскостям, то соединение называется двухсрезным и т.д.

Учитывая большие трудности, связанные с определением действительного напряженного состояния материала заклепки в зоне разрушения, для упрощения задачи принимаем, что по плоскостям среза действуют только касательные напряжения, которые распределяются по поверхности среза равномерно. Второе допущение устанавливает, что при действии статической нагрузки можно принимать поперечную силу в каждой заклепке равной

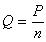где P - сила, действующая на соединение; n - число заклепок.

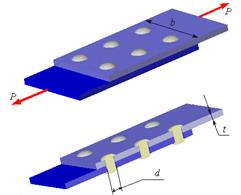
Приняв указанные допущения, получим условие прочности заклепок на срез:

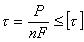
где F=πd2/4 - площадь поперечного сечения заклепки диаметром d, [τ]≈(0.6÷0.8)[σ] - допускаемое касательное напряжение. При двухсрезном или многосрезном заклепочном соединении вместо n в формулу (5.12) следует подставлять общее число срезов заклепок, расположенных по одну сторону стыка.

Кроме расчета на срез заклепочные соединения рассчитывают также на смятие. Проверяют напряжения смятия по площади соприкосновения соединяемых листов и заклепок. С целью приближенного расчета истинная эпюра распределения сжимающих напряжений смятия заменяется приближенной равномерной эпюрой (рис. 5.6). Площадь смятия одной заклепки принимают равной Fсм=dt, где t - толщина соединяемых листов.

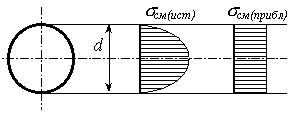
Условие прочности на смятие имеет следующие вид: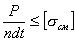

где [σсм]≈(0.5÷0.6)[σ] - допускаемое напряжение на смятие.

В случае склепывания внахлестку двух листов различной толщины надо принимать t=tmin.

Кроме расчета на срез и смятие составляют также условие прочности листа на разрыв

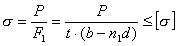
где F1 - площадь сечения листа по ряду заклепок в направлении, перпендикулярном линии действия силы P; n1 - число заклепок в этом сечении; b - ширина листа

1. Чистый изгиб: основные допущения, нормальные напряжения, зависимость между изгибающим моментом и кривизной оси изогнутой балки.

Ответ:

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым.

Определим нормальные напряжения, возникающие при чистом изгибе балки находящейся под действием моментов М_х.

В произвольной точке балки (рис.6.6, т.А) в общем случае могут возникать нормальные напряжения как вдоль продольной оси σ_z, так и вдоль поперечных осей σ_x, σ_y. Однако экспериментально установлено, что нормальные напряжения σ_x, σ_y пренебрежимо малы по сравнению с напряжениями σ_z. Принимается так называемая гипотеза ненадавливания продольных волокон σ_x = 0, σ_y = 0. Поэтому можно принять, что материал балки находится при линейном напряженном состоянии вдоль оси z, и деформации подчиняются закону Гука. То есть нормальные напряжения при изгибе можно определить из формулы .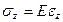

Установим закон изменения деформаций при изгибе балки. Экспериментально получено, что в деформируемой балке поперечные сечения плоские до деформации остаются плоскими и поперечными после деформации, имеет место гипотеза плоских сечений. При этом верхние волокна удлиняются, нижние укорачиваются, а продольная линия не меняет своей длины. Слой балки, не испытывающий при изгибе ни растяжения ни сжатия, называется нейтральным слоем. Линия пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией.

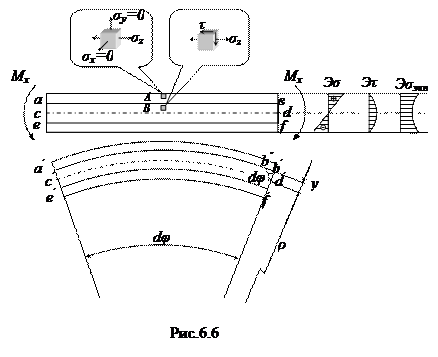Определим относительную деформацию волокна ав ε_z (далее будем обозначать ее просто ε).

,

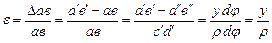где r - радиус кривизны нейтрального слоя,

у - расстояние от нейтрального слоя до рассматриваемого волокна балки.

Подставляя это соотношение в закон Гука, получим:

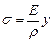(6.1)

т.е. напряжения s линейно зависят от координаты у.

Используя интегральную связь между напряжениями и изгибающим моментом

,

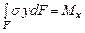подставляя в него соотношение (6.1), получим 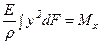, где 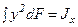- осевой момент инерции сечения.

Тогда получим выражение 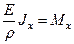, подставляя которое в (6.1) окончательно имеем формулу для нормальных напряжений при изгибе

.

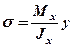Эпюра нормальных напряжений показана на рис.6.6. Как видно, на нейтральной линии они равны нулю, максимального значения напряжения достигают в крайних верхних и нижних волокнах балки.

.

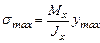Обозначая 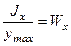, получим формулу для максимальных напряжений в произвольном сечении

,

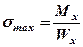где W_x – осевой момент сопротивления сечения изгибу, геометрическая характеристика поперечного сечения.

Билет №15.

1. Связь между напряжениями и внутренними силовыми факторами.

Ответ:

Нормальные и касательные напряжения в каждом поперечном сечении тела связаны определенным образом с внутренними усилиями, действующими в этом сечении. Если рассмотреть элементарную площадку dF поперечного сечения F бруса с действующими по этой площадке напряжениями s, t_х, t_у, получим, что на площадку dF действуют элементарные силы s dF, t_хdF t_уdF. Тогда можно записать следующие интегральные зависимости:

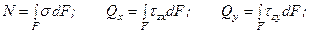
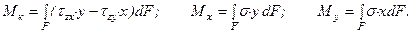
1. Расчёт сварных соединений.

Ответ:

Исходя из принципа равнопрочности сварного стыка и основного металла, а также принимая во внимание, что сварное соединение весьма часто разрушается по основному металлу, нормативное сопротивление (предел текучести) сварного соединения принимают таким же, как для основного металла.

Одинаковыми с основным металлом принимаются и коэффициенты однородности для соединений стыковыми швами, выполненных автоматической сваркой. В случае ручной сварки шлакообразующими электродами коэффициенты однородности соединений в стык в растянутых элементах принимаются одинаковыми с основным металлом только при плотных швах, плотность которых гарантирована специальными мерами контроля над качеством швов; последнее обязательно для ответственных конструкций, особенно работающих на динамическую нагрузку, Если отсутствует специальный контроль, то ввиду большого рассеяния величин прочности сварки для стыковых швов, работающих на растяжение, коэффициент однородности принимается более низкий, чем для основного металла (порядка 0,75). Для сжатых элементов, где небольшая пористость швов не имеет существенного значения, величины коэффициентов однородности принимаются такими же, как для основного металла. В результате для расчета соединений в стык, выполненных ручной сваркой шлакообразующими электродами, получаются два расчетных сопротивления осевым усилиям, равных для конструкций из малоуглеродистой стали: 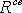= 0,9-24 = 21 кг/мм2 для сжатых элементов, а также для растянутых элементов при специальных мерах контроля (что совпадает с расчетным сопротивлением основного металла) и 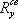= 0,75-24 = 18 кг/мм2 для растянутых элементов при отсутствии специальных мер контроля. Для конструкций из низколегированных сталей соответствующие величины расчетных сопротивлений составляют 29 и 25 кг/мм2.

Расчетное сопротивление срезу принимается при расчете соединений в стык таким же, как для основного металла: 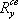= 13 кг/мм2 для конструкций из малоуглеродистой стали и 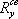=17 кг/мм2 для конструкций из низколегированной стали.

1. Жёсткость и податливость поперечного соединения.

Ответ:

Жёсткость – это способность тела или конструкции сопротивляться деформации.

Кривизна нейтрального слоя изогнутой оси балки прямо пропорциональна изгибающему моменту и обратно пропорциональна величине 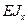, называемой жёсткостью сечения балки при изгибе.

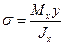
Формула выведена для чистого изгиба бруса, при котором во всех поперечных сечениях момент 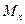одинаков. При поперечном изгибе в сечениях кроме изгибающего момента возникают поперечные силы и, следовательно, касательные напряжения. Поперечные силы вызывают сдвиг сечений, при этом сечения искривляются, а продольные волокна давят одно на другое.

Билет №16.

1. Дифференциальные уравнения равновесия бруса с прямолинейной осью.

Ответ:

Рассмотрим решение задачи об устойчивости сжатого стержня. Пусть стержень, оба конца которого закреплены шарнирно, сжат силой Р_кр (рис.9.2). Стержень искривился так, что в сечении z прогиб составил δ. Приближенное дифференциальное уравнение изогнутой оси балки имеет вид:

.

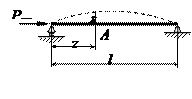
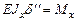Изгибающий момент в сечении z в изогнутом состоянии равен моменту силы Р_кр, но обратного направления, а, следовательно, и знака

.

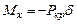Тогда дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости будет

.

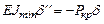Обозначая 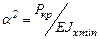(9.1) получим линейное дифференциальное уравнение второго порядка относительно прогиба δ

.

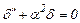Его общее решение имеет вид

,

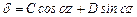где С и D – постоянные интегрирования, определяемые из условий на опорах. На опорах стержня прогиб равен нулю, т.е. 1) при z=0, δ=0;

2) при z=l, δ=0. Подставляя первое условие в уравнение прогибов получим С=0, из второго условия получим .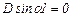

Последнее соотношение справедливо при 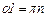, где n – любое целое число.

Откуда 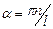, с учетом принятого ранее обозначения (9.1), получим .

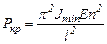Минимальное действительное значение критической силы получится при n=1

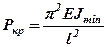. (9.2)

Это и есть формула Эйлера для критической силы.

Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной

.

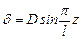1. Энергия деформации при сдвиге.

Ответ:

Удельной потенциальной энергией деформации u называется величина потенциальной энергии деформации U, накопленной в единице объема тела V. Для линейного напряженного состояния:

.

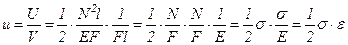Используя принцип независимости действия сил, полученный результат можно обобщить на случай объемного напряженного состояния:

.

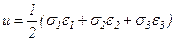В случае площадок общего положения (не главных площадок) выражение для удельной потенциальной энергии приобретает вид:

.

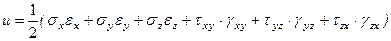Предыдущее выражение можно преобразовать с помощью формул обобщенного закона Гука к виду:

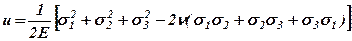. (3.5)

Рассмотрим напряженное состояние чистого сдвига. Запишем выражение удельной потенциальной энергии деформации по площадкам чистого сдвига:

.

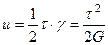С другой стороны чистый сдвиг - это двухосное напряженное состояние с главными напряжениями 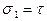; 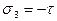, поэтому можно записать u как

.

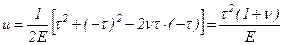Очевидно, величина удельной потенциальной энергии деформации u не должна зависеть от того по каким площадкам она записана, поэтому 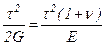, откуда, как упоминалось ранее .

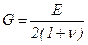Таким образом, постоянные упругости материалов, характеризующие жесткость при растяжении и сдвиге и поперечную деформацию, являются зависимыми. Поэтому достаточно определить лабораторным путем при растяжении две характеристики упругости Е и n, а третья G может быть вычислена аналитически.

1. Внутренние силовые факторы в поперечных сечениях балок при плоском поперечном изгибе.

Ответ: