Центральное растяжение-сжатие

2.1 Продольные силы

1. Внутреннее усилие в поперечном сечении при центральном растяжении

+: продольная сила

–: поперечная сила

–: изгибающий момент

–: крутящий момент

2. Продольная сила в указанном поперечном сечении

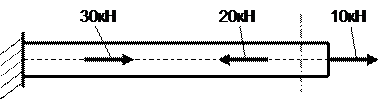
+: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

3. Продольная сила в указанном поперечном сечении

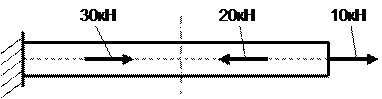
+: - 10 кН

-: 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

4. Продольная сила в указанном поперечном сечении

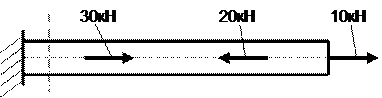
-: - 10 кН

-: 10 кН

+: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

5. Продольная сила в указанном поперечном сечении

+: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

6. Продольная сила в указанном поперечном сечении

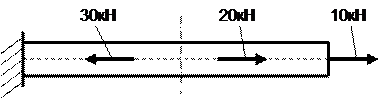
-: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

+: 30 кН

-: - 30 кН

7. Продольная сила в указанном поперечном сечении

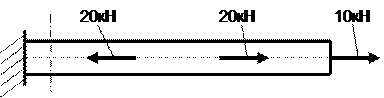
+: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

8. Продольная сила в поперечном сечении (а) стержня

+: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

9. Продольная сила в поперечном сечении (а) стержня

-: 10 кН

+: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

10. Продольная сила в поперечном сечении (b) стержня

+: 10 кН

-: - 10 кН

-: 20 кН

-: - 20 кН

-: 30 кН

-: - 30 кН

2.2 Напряжения при растяжении (сжатии)

1. Рациональное поперечное сечение бруса при растяжении (площадь сечений одинакова)

+: Форма не имеет значения

–: Круглое

–: Квадратное

–: Двутавр

–: Швеллер

2. Формула для определения нормальных напряжений в брусе при растяжении-сжатии:

+:

–:

–:

–:

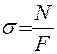
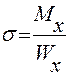
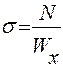
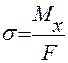
3. Условие прочности при растяжении (сжатии)

+:

–:

–:

–:

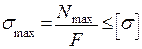
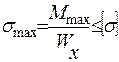
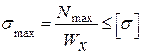
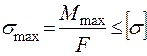
4. Напряжение в поперечных сечениях бруса при растяжении

–: Касательное равномерное

+: Нормальное равномерное

–: Касательное неравномерное

–: Нормальное неравномерное

5. Напряжение в поперечном сечении стержня

+: 5 кН/см²

-: - 5 кН/см²

-: - 45 кН/см²

-: 45 кН/см²

6. Напряжение в поперечном сечении стержня

-: 5 кН/см²

+: – 5 кН/см²

-: – 45 кН/см²

-: 45 кН/см²

7. Напряжение в поперечном сечении стержня

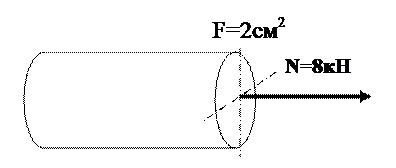
-: – 4 кН/см²

+: 4 кН/см²

-: - 16 кН/см²

-: 16 кН/см²

8. Напряжение в поперечном сечении стержня

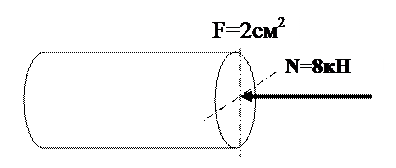
+: – 4 кН/см²

-: 4 кН/см²

-: – 16 кН/см²

-: 16 кН/см²

9. Напряжение в поперечном сечении стержня

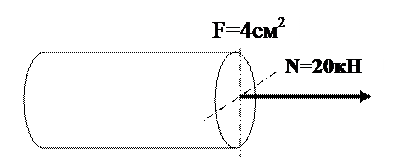
+: 5 кН/см²

-: -5 кН/см²

-: - 80 кН/см²

-: 80 кН/см²

10. Напряжение в поперечном сечении стержня

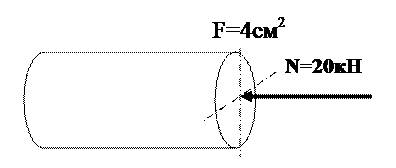
+: - 5 кН/см²

-: 5 кН/см²

-: - 80 кН/см²

-: 80 кН/см²

2.3 Деформации при растяжении

1. Формула для абсолютного удлинения бруса при растяжении

+:

–:

–:

–:

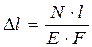
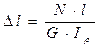
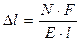
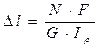
2. Относительная продольная деформация на участке (I) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

+: 0,005

-: - 0,005

-: 0,002

-: - 0,002

-: 0,001

-: - 0,001

3. Относительная продольная деформация на участке (I) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

-: 0,005

+ - 0,005

-: 0,002

-: - 0,002

-: 0,001

-: - 0,001

4. Относительная продольная деформация на участке (II)

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

- - 0,005

- 0,005

-: 0,002

-: - 0,002

+: 0,01

-: - 0,01

5. Относительная продольная деформация на участке (II) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=100кН

EF2=200кН

+: 0,005

- - 0,005

-: 0,002

-: - 0,002

-: 0,001

-: - 0,001

6. Относительная продольная деформация на участке (II) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=100кН

EF2=200кН

+: - 0,005

- 0,005

-: 0,002

-: - 0,002

-: 0,001

-: - 0,001

7. Относительная продольная деформация на участке (II) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

+: - 0,01

-: 0,01

-: - 0,005

- 0,005

-: 0,002

-: - 0,002

8. Относительная продольная деформация на участке (III) стержня

EF3=600кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

+: 0,01

-: - 0,01

-: - 0,005

- 0,005

-: 0,002

-: - 0,002

9. Относительная продольная деформация на участке (III) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

+: 0,01

-: - 0,01

-: - 0,005

- 0,005

-: 0,002

-: - 0,002

10. Относительная продольная деформация на участке (III) стержня

EF3=400кН

P1=1кН

P3=3кН

P2=2кН

II

I

III

EF1=200кН

EF2=300кН

+: - 0,005

- 0,005

-: 0,002

-: - 0,002

-: 0,001

-: - 0,001

2.4 Поперечная деформация. Коэффициент Пуассона

1. Формула для определения относительной поперечной деформации стержня

+:

–:

–:

–:

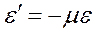
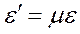
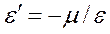
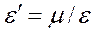
2. Величина коэффициента Пуассона определяется

+: типом материала

–: характером деформирования

–: видом напряженного состояния

–: интенсивностью нагрузки

3. Величина коэффициента Пуассона μ находится в интервале

+: 0 < μ < 0.5

–: - 0.5 < μ < 0

–: - 2 < μ < -1

–:1 < μ < 2

4. Коэффициент Пуассона является характеристикой

+: упругости

–: пластичности

–: прочности

–: устойчивости

5. Коэффициент Пуассона связывает величину поперечной деформации с величиной

+: продольной деформации

–: нормальных напряжений

–: касательных напряжений

–: прогиба

–: угла закручивания

6. Величина поперечной деформации стержня по знаку

+: противоположна величине продольной деформации

–: совпадает с величиной продольной деформации

–: всегда положительна

–: всегда отрицательна

–: определяется видом материала

2.5 Диаграмма растяжения. Основные характеристики диаграммы растяжения

1. Предел прочности – это:

+: Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца

–: Напряжение, при котором деформации растут без увеличения нагрузки

–: Наибольшее напряжение, при котором справедлив закон Гука

–: Наибольшее напряжение, при котором отсутствуют пластические деформации

2. Предел текучести – это:

–: Наибольшее напряжение, при котором справедлив закон Гука

–: Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца

+: Напряжение, при котором деформации растут без увеличения нагрузки

–: Наибольшее напряжение, при котором отсутствуют пластические деформации

3. Предел пропорциональности – это:

+: Наибольшее напряжение, при котором справедлив закон Гука

–: Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца

–: Напряжение, при котором деформации растут без увеличения нагрузки

–: Наибольшее напряжение, при котором отсутствуют пластические деформации

4. Характеристика материала, определяемая статическими испытаниями образцов на растяжение

–: Твердость

–: Предел выносливости

+: Предел прочности

–: Ползучесть

5. Отношение наибольшей силы, которую выдерживает образец, к площади его поперечного сечения

–: Предел текучести

–: Предел выносливости

+: Предел прочности

–: Предел пропорциональности

6. Напряжение, при котором происходит рост деформации без заметного увеличения нагрузки

+: Предел текучести

–: Предел выносливости

–: Предел прочности

–: Предел пропорциональности

7. Наибольшее напряжение, при котором сохраняется пропорциональная зависимость между нагрузкой и удлинением

–: Предел текучести

–: Предел выносливости

–: Предел прочности

+: Предел пропорциональности

2.6 Закон Гука. Модуль упругости.

1. Модуль упругости Е - это:

–: Коэффициент пропорциональности между продольными перемещениями и силами

–: Коэффициент пропорциональности между продольными силами и перемещениями

+: Коэффициент пропорциональности между нормальными напряжениями и линейными деформациями

–: Коэффициент пропорциональности между линейными деформациями и нормальными напряжениями

2. Модуль упругости материала стержня

+:20000 кН/см²

–:10000 кН/см²

–:50000 кН/см²

–:12500 кН/см²

3. Абсолютное удлинение бруса при растяжении

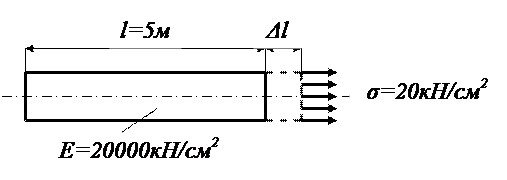
+: 0,005 м

–: – 0,005 м

–: – 0,001 м

–: 0,001 м

–: – 0,002 м

–: 0,002 м

4. Относительная деформация бруса при растяжении

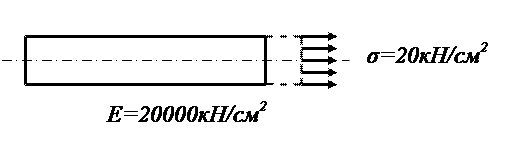
+: 0,001

-: - 0,001

-: 0,004

-: - 0,004

5. Относительная деформация бруса при сжатии

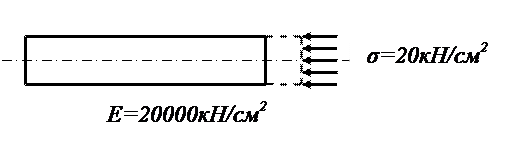
-: 0,001

+: - 0,001

-: 0,004

-: - 0,004

6. Относительная деформация бруса при растяжении

+: 0,001

-: - 0,001

-: 0,004

-: - 0,004

7. Относительная деформация бруса при сжатии

+: -0,001

-: 0,001

-: 0,004

-: - 0,004