Магнитожидкостная цепочка с упругостью пондеромоторного типа
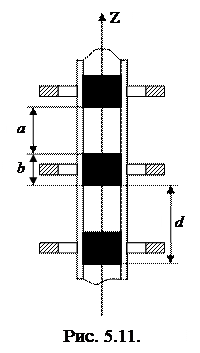
При помощи промодулированного в пространстве магнитного поля можно сформировать систему «жидкостная цепочка» (ЖЦ). Звенья ЖЦ представляют собой капли жидкости, а соединяющими элементами являются упругие газовые полости. На рисунке 5.11 изображена модель такой системы в виде прерывистого жидкостного столбца. Цепочка магнитожидкостных капель стабилизирована системой кольцевых магнитов, расположенных соосно с трубкой и отстоящих друг от друга на d. Система перемычек заключена в абсолютно жесткую цилиндрическую оболочку с постоянным поперечным сечением S; b – длина жидкостного звена, a – толщина газовой полости, d – период идентичности.
 Предполагается, что в цепочке распространяется только продольная звуковая волна (нулевая мода), процессы вязкого трения и теплообмена отсутствуют, жидкость несжимаемая. В таком приближении данная задача решена В.М. Полуниным и Е.Б. Постниковым в 2001 г.
Предполагается, что в цепочке распространяется только продольная звуковая волна (нулевая мода), процессы вязкого трения и теплообмена отсутствуют, жидкость несжимаемая. В таком приближении данная задача решена В.М. Полуниным и Е.Б. Постниковым в 2001 г.
При отсутствии теплообмена в системе процесс распространения упругих волн будет носить адиабатный характер. Смещения жидкостных звеньев из положения равновесия подчиняются гармоническому закону, их значения соответственно по номеру обозначим как Un-1, Un, Un+1.
На упругие свойства системы ЖЦ оказывает влияние газовая и магнитоупругая составляющая, обусловленная взаимодействием магнитной жидкости с источником магнитного поля. Смещение границы раздела фаз U вызвано параллельным действием обоих факторов упругости, поэтому коэффициент квазиупругой силы системы k равен сумме коэффициентов магнитоупругой и газовой полости: k=kр+kg.
Будем считать, что в цепочке распространяется только продольная звуковая волна (нулевая мода), процессами вязкого трения и теплообмена пренебрегаем, жидкость полагаем несжимаемой.
В этом случае к силам, действующим на каплю с номером n со стороны воздушных полостей 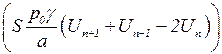 , добавляется пондеромоторная сила, действующая на эту каплю со стороны магнитного поля при ее смещении из положения равновесия.
, добавляется пондеромоторная сила, действующая на эту каплю со стороны магнитного поля при ее смещении из положения равновесия.
При условии совпадения положения равновесия с плоскостью симметрии магнита эта сила равна:
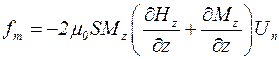 . (5.101)
. (5.101)
В результате второй закон Ньютона для этой капли принимает вид:
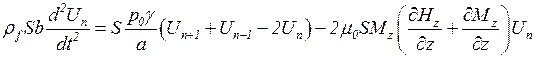 . (5.102)
. (5.102)
Вводя обозначение 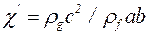 , а также
, а также 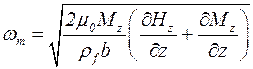 для циклической частоты колебаний капли под действием пондеромоторных сил, запишем уравнение, описывающие распространение волн в цепочке:
для циклической частоты колебаний капли под действием пондеромоторных сил, запишем уравнение, описывающие распространение волн в цепочке:
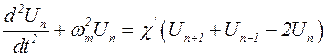 . (5.103)
. (5.103)
Уравнение (5.103) имеет вид стандартного уравнения связанных взаимодействующих осцилляторов. Известно, что его решение имеет вид бегущей волны:
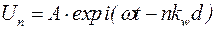 , (5.104)
, (5.104)
причем частота и волновое число связаны дисперсионным уравнением:
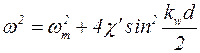 . (5.105)
. (5.105)
Анализ уравнения (5.105) приводит к заключению, что в рассматриваемой системе при возбуждении в ней волн с частотой w распространяются лишь те, длина волны которых попадает в «область прозрачности»:
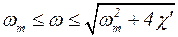 (5.106)
(5.106)
Данная магнитожидкостная цепочка работает как полосовой фильтр звуковых колебаний. На достаточное расстояние распространяются только возмущения с частотами из «окна» (5.106), прочие же экспоненциально затухают с расстоянием от источника. Действие колебательной системы эквивалентно лестничному полосовому LC-фильтру.
Сравнение упругих свойств газовой и магнитной подсистем производится на основе параметра y:
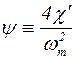 . (5.107)
. (5.107)
В предположении, что магнитная восприимчивость МЖ равна единице, будем иметь:
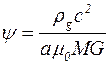 , (5.108)
, (5.108)
где rg – плотность газа; с – скорость звука в газе; М – намагниченность жидкости; G – градиент напряженности магнитного поля; m0 – магнитная постоянная.
Принимая во внимание полученные нами данные для поля кольцевого магнита, при М=20 кА/м, G=4,5×106 А/м2, rg=1,29 кг/м3, с=340 м/с, а=0,1 м, пользуясь выражением (5.108), находим: y»13.
При увеличении "а" на порядок вклады магнитной и газовой упругости становятся близкими друг к другу. Если же y>>1, то роль магнитной упругости мала, а назначение магнитного поля заключается лишь в поддержании формы МЖ–капли.
