III. Работа над новым материалом. Для подготовки к рассмотрению алгоритма проверки деления умножением полезно
Для подготовки к рассмотрению алгоритма проверки деления умножением полезно повторить правило:
Если умножить частное на делитель, то получится делимое.
Для этого можно записать на доске заранее примеры вида:
56 : 7 80 : 20 100 : ? = 50
Решая эти примеры, вызванные к доске ученики должны не только записать ответ, но и дать объяснение:
56 : 7 = 8, так как 8 · 7 (или 7 · 8) равно 56 (56 разделить на 7, получится 8, так как если 8 умножить на 7, получится 56);
80 : 20 = 4, так как 20 · 4 = 80 (или 4 · 20).
После этого следует сформулировать уже хорошо знакомую детям взаимосвязь между компонентами деления и сказать, что на ее использовании основана проверка правильности выполнения действия деления.
После такой подготовки предложить учащимся прочитать объяснение, данное в учебнике, и объяснить тот пример, которым оно проиллюстрировано.
78 : 3 = 26
Дети. Частное умножаю на делитель: 26 · 3 = 78. Сравниваю полученный результат с делимым: 78 = 78. Эти числа равны, значит, деление выполнено верно.
Полезно, чтобы 2–3 раза основные этапы проверки деления умножением были повторены вызванными учениками (один ученик объясняет, что делает сначала, другой – что потом, третий делает вывод). Объяснение всегда должно вестись на конкретном примере.
Для первичного закрепления с пояснениями выполняется задание № 1 (комментирование см. выше).
После этого (на основе изученной ранее связи между числами при делении и проверки деления) учащиеся рассматривают и объясняют решение уравнения из задания № 2.
З а д а н и е № 2.
х : 2 = 14
Дети. Неизвестно делимое. Чтобы найти делимое, надо частное умножить на делитель:
х = 14 · 2
х = 28
28 : 2 = 14
14 = 14
IV. Игротека.
V. Работа над пройденным материалом.
1. Решение задач. Перед решением задачи № 4 учитель вместе с детьми записывает на доске краткую запись:
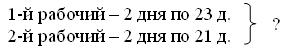
После этого дети должны заметить, что задачу можно решить двумя разными способами.
I способ:
1) 23 + 21 = 44 (д.) – 2 рабочих за 1 день
2) 44 · 2 = 88 (д.)
II способ:
1) 23 · 2 = 46 (д.) – 1-й рабочий за 2 дня
2) 21 · 2 = 42 (д.) – 2-й рабочий за 2 дня
3) 46 + 42 = 88 (д.)
О т в е т: всего 88 деталей за 2 дня.
Затем учащиеся записывают решение задачи самостоятельно любым способом.
Задачу № 5 можно предложить учащимся решить самостоятельно. Учитель оказывает помощь детям, которые затрудняются в решении задачи.
2. Задание № 6 (1, 2) учащиеся выполняют с комментированием у доски. Оно подготавливает учащихся к введению новой темы «Деление с остатком».
№ 6 (1).
Запишите числа от 19 до 30 и подчеркните те из них, которые делятся на 4 без остатка.
№ 6 (2).
Запишите числа от 20 до 30 и подчеркните те из них, которые делятся на 3 без остатка.
3. Для самостоятельной работы на уроке учащимся можно предложить задание № 7.
VI. Итоги урока.
Учитель. Ребята, над чем работали сегодня на уроке?
Учащиеся. Сегодня на уроке мы учились выполнять проверку деления.
Учитель. Что повторяли вы сегодня на уроке?
Учащиеся. Решали задачу двумя способами, решали примеры и уравнения.
Домашнее задание:с. 15, № 7.
У р о к 14. ПРИЕМ ДЕЛЕНИЯ ДЛЯ СЛУЧАЕВ ВИДА
87 : 29; 66 : 22 (с. 16)
Цели: познакомить учащихся с новым приемом внетабличного деления; закреплять ранее изученные случаи внетабличного умножения и деления; совершенствовать навык решения задач и уравнений.
Ход урока
I. Организационный момент.
II. Устный счёт.
В устный счет на уроке включить задание «Расшифруй» (внизу страницы) и задание № 15 на с. 22.
1. Задание «Расшифруй»
14 · 4 7 · 6 18 · 3 8 · 9 16 · 6 7 · 14 27 · 2 9 · 7 5 · 16









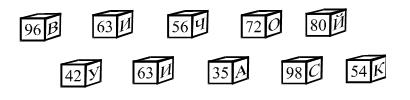
2. Между некоторыми цифрами 1 2 3 4 5, не переставляя их, поставьте знаки действий и, если нужно, скобки так, чтобы значение выражения стало равно: 1) 40; 2) 80.
