Магнитокалорический эффект в нанодисперсной магнитной системе
Магнитокалорический эффект – изменение температуры магнитного вещества при его адиабатном намагничивании или размагничивании.
В переменном однородном магнитном поле температура МЖ колеблется около равновесного значения вследствие магнитокалорического эффекта. Под влиянием теплового расширения объем жидкости также будет испытывать колебания. Определим вклад этого процесса в генерацию упругих колебаний [1].
Пусть магнитное поле, временная зависимость которого задается уравнением H=Ho+Hm×coswt, направлено вдоль плоскопараллельного слоя МЖ. Амплитуда переменной составляющей магнитного поля мала настолько, что выполняется условие Hm<<Ho. При изотермическом наложении магнитного поля, для которого Hn=0, не возникает перепада давления на границе жидкость – вакуум. Однако в случае адиабатного процесса на границе МЖ – вакуум возникает скачок давления, в результате чего при свободной поверхности раздела происходит деформация жидкости. Покажем это. Дифференциал энтальпии Э может быть представлен в виде
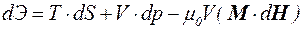 . (4.1)
. (4.1)
Откуда следует
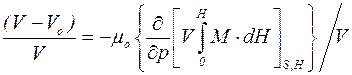 . (4.2)
. (4.2)
Амплитуда деформации жидкости dVm/V при наложении поля Hm может быть получена следующим образом:
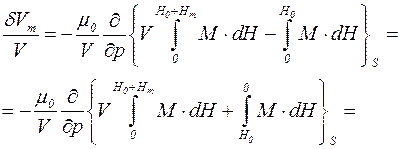
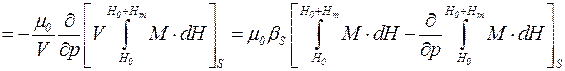 (4.3)
(4.3)
В силу неравенства Hm<<Ho можно принять М=const=Mo, тогда
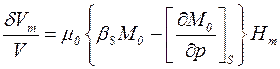 . (4.4)
. (4.4)
Совершим переход от р к плотности r, пользуясь линейным уравнением состояния:
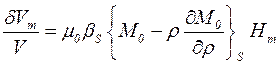 . (4.5)
. (4.5)
При отсутствии релаксации приращение намагниченности при выбранной ориентации вектора H может быть представлено в виде
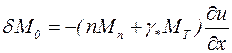 . (4.6)
. (4.6)
Воспользовавшись уравнением непрерывности в форме 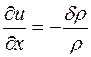 , получим
, получим 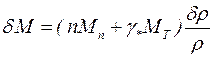 , откуда
, откуда
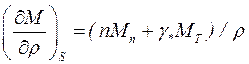 . (4.7)
. (4.7)
Подставляя выражение (4.7) в формулу (4.6), находим
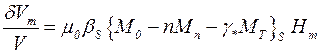 . (4.8)
. (4.8)
Если Mo~n, что выполняется, например, для системы ФЧ, намагничивание которой описывается формулой Ланжевена, то nMn=Mo и
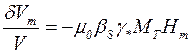 . (4.9)
. (4.9)
Приведем известное в теории магнетизма соотношение для магнитокалорического эффекта:
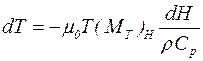 . (4.10)
. (4.10)
Поэтому формулу (4.8) можно представить иначе:
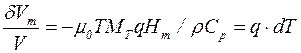 . ( 4.11)
. ( 4.11)
В переменном магнитном поле вследствие магнитокалорического эффекта и свойственного жидкости теплового расширения происходят колебания объема жидкости с частотой изменения поля.
Магнитокалорический эффект выполняет в данном случае функцию одного из возможных механизмов электромагнитного возбуждения упругих колебаний в МЖ. Зависимость амплитуды колебаний от Н определяется множителем МТ в выражении (4.8). Предполагая, что намагничивание жидкости происходит в соответствии с функцией Ланжевена, получаем
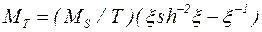 (4.12)
(4.12)
и, следовательно,
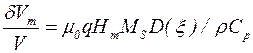 , (4.13)
, (4.13)
где 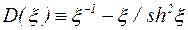 .
.
На рисунке 4.1 показана зависимость относительного изменения величины bξ (прерывистая кривая) и амплитуды упругих колебаний МЖ -ba (сплошная кривая) от напряженности поля Н0.
Зависимость bx(Н) построена в предположении, что m*=2,5×10-19 А×м2 и Т=290 К. Функция D(x) имеет один максимум в точке Н=25,4 кА/м, при этом ее числовое значение составляет 0,348.
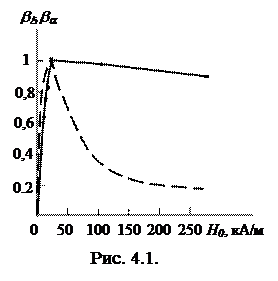 Для оценки dVm/V воспользуемся значениями D(x)=0,35, MS=50 кА/м, Hm=1,5 кА/м, q=0,64×10-3 К-1, r=1250 кг/м3, Ср=2100 Дж/кг×К, подставив которые в выражение (4.6), получаем dVm/V=0,8×10-8.
Для оценки dVm/V воспользуемся значениями D(x)=0,35, MS=50 кА/м, Hm=1,5 кА/м, q=0,64×10-3 К-1, r=1250 кг/м3, Ср=2100 Дж/кг×К, подставив которые в выражение (4.6), получаем dVm/V=0,8×10-8.
Однако экспериментальное значение статической деформации 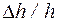 составляет 0,8·10-7, что на порядок превосходит полученную оценку деформации за счет магнитокалорического эффекта. На рисунке 4.1 сплошной линией показана экспериментальная кривая зависимости относительной амплитуды
составляет 0,8·10-7, что на порядок превосходит полученную оценку деформации за счет магнитокалорического эффекта. На рисунке 4.1 сплошной линией показана экспериментальная кривая зависимости относительной амплитуды 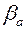 от напряженности магнитного поля H, полученная по данным для образца МЖ на основе магнетита и масла МВП на частоте 2МГц. Положения максимумов теоретической и экспериментальной кривых близки между собой, однако нисходящие ветви их существенно отличаются друг от друга.
от напряженности магнитного поля H, полученная по данным для образца МЖ на основе магнетита и масла МВП на частоте 2МГц. Положения максимумов теоретической и экспериментальной кривых близки между собой, однако нисходящие ветви их существенно отличаются друг от друга.
По-видимому, магнитокалорический эффект в МЖ на основе магнетита не может играть основную роль в электромагнитном возбуждении упругих колебаний в мегагерцовом диапазоне частот.
Наряду с эффектом выделения или поглощения тепла при перемагничивании жидкости, обусловленного выстраиванием ферромагнитных диполей по полю, происходит выделение или поглощение тепла, вызванное собственным магнитокалорическим эффектом ферромагнитной фазы. Оценим его вклад в изменение объема жидкости.
Количество теплоты, выделяемой при намагничивании одной частицы 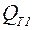 , получим, воспользовавшись выражением (4.10), которое после преобразований дает
, получим, воспользовавшись выражением (4.10), которое после преобразований дает
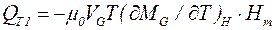 , (4.14)
, (4.14)
где G – индекс твердого ферромагнетика.
Объем твердой фазы МЖ составляет 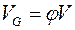 , поэтому тепло, выделяемое в объеме дисперсной системы, может быть найдено из выражения
, поэтому тепло, выделяемое в объеме дисперсной системы, может быть найдено из выражения
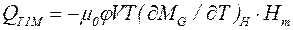 . (4.15)
. (4.15)
Или в расчете на единицу массы жидкости
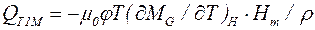 . (4.16)
. (4.16)
Выражение (4.16) позволяет получить приращение температуры жидкости
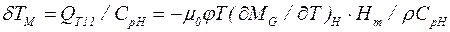 , (4.17)
, (4.17)
где СрH – удельная теплоемкость при p=const и Н=const.
Относительное приращение объема:
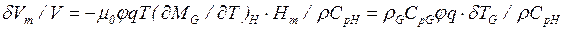 (4.18)
(4.18)
В ферромагнетиках магнитокалорический эффект достигает максимума в точке Кюри 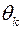 . Если, например, в качестве магнитной фазы выбрать гадолиний – Gd, для которого qk=293 К, то можно получить большой магнитокалорический эффект вблизи комнатной температуры. По данным работы К.П. Белова и сотрудников, при H0=200 кА/м,
. Если, например, в качестве магнитной фазы выбрать гадолиний – Gd, для которого qk=293 К, то можно получить большой магнитокалорический эффект вблизи комнатной температуры. По данным работы К.П. Белова и сотрудников, при H0=200 кА/м, 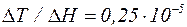 К·м/А, r=7,98∙103 кг/м3, CpG=320 Дж/(кг·К). Следовательно, при Hm=1,5 кА/м
К·м/А, r=7,98∙103 кг/м3, CpG=320 Дж/(кг·К). Следовательно, при Hm=1,5 кА/м 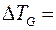 3,75∙10-3 К и
3,75∙10-3 К и 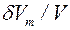 =0,35∙10-6, что почти на два порядка выше результата, даваемого магнитокалорическим эффектом выстраивания диполей в жидкости на основе магнетита и керосина.
=0,35∙10-6, что почти на два порядка выше результата, даваемого магнитокалорическим эффектом выстраивания диполей в жидкости на основе магнетита и керосина.
