Пондеромоторный механизм возбуждения колебаний в цилиндрическом резонаторе с магнитной жидкостью

Воздействие электромагнитного поля на магнитную жидкость может привести к возникновению в ней различного рода колебаний: упругих, поверхностных, колебаний формы. Особое место среди них занимают упругие – звуковые и ультразвуковые колебания, научный интерес к которым не вызывает сомнений. Преобразовательный эффект такого рода мы будем называть магнитоакустическим эффектом (МАЭ).

В прикладном отношении МЖ в рамках рассматриваемой проблемы выступает в качестве материала, при помощи которого осуществляются превращение энергии электромагнитного поля в энергию упругих колебаний. При этом преобразующие устройства обладают рядом преимуществ по сравнению с традиционными твердотельными магнитострикционными и пьезоэлектрическими преобразователями. Эти преимущества заключаются в следующем: рабочее тело преобразователя по сравнению с твердотельным имеет меньшую плотность и скорость звука, что более чем на порядок уменьшает массу излучателя при одинаковой резонансной частоте; поверхность МЖ способна приобретать любую геометрию, задаваемую формой контейнера; возможна плавная перестройка резонансной частоты и диаграммы направленности; равенство волновых сопротивлений МЖ и морской воды предопределяет возможность создания широкополосного источника звуковых колебаний.

Первые попытки решения этой задачи основывались на применении грубых ферросуспензий. Однако, в связи с быстрым расслаиванием таких систем и очень большим затуханием упругих колебаний в них, такого рода преобразователи не могли найти применение. Перечисленных недостатков лишены преобразователи, активными элементами, в которых являются МЖ. Впервые проблемы электромагнитного возбуждения акустических колебаний в МЖ рассмотрены в теоретической работе B. Cary и F. Fenlon. Активный элемент рассматриваемого ими преобразователя имеет форму цилиндрического диска – таблетки. Анализируется случай бесконечного плоскопараллельного слоя, по нормали к которому направлено внешнее магнитное поле. Путем термодинамических преобразований показано, что на границах слоя возникает перепад давлений, обусловленный скачком напряженности магнитного поля. В области технического насыщения допускается возможность функционирования лишь пондеромоторного механизма, с чем связываются надежды на получение источника колебаний, конкурирующего с традиционными магнитострикционными и пьезоэлектрическими преобразователями в диапазоне 100-150 кГц, в котором неэлектропроводные МЖ характеризуются невысокими потерями на вихревые токи и перемагничивание.

Первые результаты экспериментального изучения особенностей функционирования магнитожидкостных преобразователей получены белорусскими учеными А.Р. Баевым и П.П. Прохоренко на частотах 16-26,7 кГц.

В том случае, когда МЖ заполняет полость с определенной геометрией – резонатор, может быть использован простейший источник магнитного поля, основным назначением которого является создание переменной составляющей поля. Резонансное возбуждение колебаний достигается путем подбора частоты изменения вынуждающей силы.

Решению этой задачи посвящены работы В.М. Полунина (1978 г.), в которых рассматривается цилиндрическая модель магнитожидкостного излучателя (МЖИ). В простейшем случае эта модель может быть реализована погружением прямолинейного проводника, по которому протекает переменный ток, в МЖ.

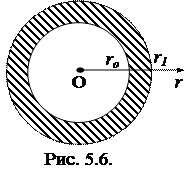В теоретическом аспекте преимущество данной модели состоит в том, что для ее аналитического рассмотрения не возникает необходимости в использовании какой-либо эмпирической или полуэмпирической формулы, определяющей геометрию и временную зависимость магнитного поля. Рассматриваемое магнитное поле – это поле прямолинейного бесконечного проводника с током, геометрия которого, определяемая законом Био-Савара-Лапласа, хорошо известна. Сущность метода изучается на модели, представленной на рисунке 5.6.

Данный метод возбуждения резонансных колебаний в МЖ основан на применении неоднородного магнитного поля, содержащего изменяющуюся во времени по гармоническому закону компоненту. МЖ заполняет пространство между коаксиальными бесконечно длинными цилиндрическими поверхностями, радиусы, которых равны r_o и r₁. В предлагаемой модели используется невязкая, нетеплопроводная и однородная жидкость, особенность намагничивания, которой будет отмечена ниже.

Ограничивающие жидкость цилиндры считаются немагнитными, неэлектропроводными и абсолютно жесткими. Допущение об электрической и магнитной «нейтральности» ограничивающих цилиндров позволяет пренебречь электромагнитной индукцией в них и всеми вытекающими последствиями.

В используемой цилиндрической системе координат ось Z совпадает с осью цилиндров и направлена за чертеж. Волновое уравнение, описывающее смещение частиц жидкости из положения равновесия в цилиндрических координатах, принимает вид

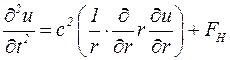, (5.2)

где u(r,t) – смещение частиц от положения равновесия;

r – координата;

t – время;

с – скорость распространения звука в жидкости, являющаяся действительной величиной, поскольку отсутствуют диссипативные процессы, обусловленные вязкостью или теплопроводностью среды;

F_н – вынуждающая сила, которая в рассматриваемой модели связана с неоднородностью магнитного поля, создаваемого осевым током в неэлектропроводной среде.

Правая часть уравнения (5.2) представляет собой отношение силы упругости, действующей на элементарный объем жидкости dV, к массе заключенной в нем жидкости. При наложении неоднородного магнитного поля на объем dV неэлектропроводной МЖ будет действовать пондеромоторная сила 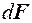, величина и направление, которой могут быть получены в рамках квазистатической гидродинамики изотропной МЖ по формуле:

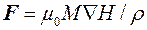. (5.3)

Вынуждающая сила в рассматриваемой модели существенно зависит от вида функции 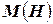, т.е. от конкретного вида уравнения магнитного состояния, которое в свою очередь должно удовлетворять уравнениям Максвелла 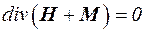и .

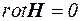С этим требованием согласуется, в частности, линейное уравнение

M=cH, (5.4)

где c – магнитная восприимчивость, и уравнение магнитного насыщения

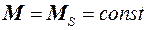. (5.5)

В первом случае на единицу массы будет действовать дополнительная сила F_м, равная

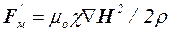. (5.6)

Во втором случае:

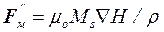. (5.7)

Чтобы обеспечить цилиндрическую симметрию решаемой задачи, используется магнитное поле, создаваемое бесконечным проводником с током, расположенным вдоль оси ОZ. Зависимость тока I от времени задана в виде

I=I₀+I_mּcoswt, (5.8)

где I₀ и I_m – постоянная компонента тока и амплитуда переменной компоненты тока соответственно;

w – круговая частота переменного тока.

В квазистатическом приближении на основе закона Био-Савара-Лапласа получим для H следующее выражение:

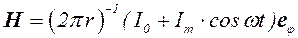, (5.9)

где 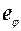– вектор-орт.

Подставляя (5.5) в (5.2) и (5.3), найдем проекцию силы 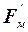и 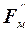на направление вектора-орта:

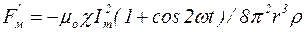; (5.10)

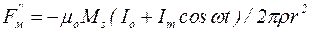. (5.11)

Причем при получении (5.11) предполагается, что амплитуда переменной составляющей тока значительно меньше постоянной составляющей, т.е. 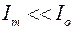, а при получении (5.6) – I_o=0. Из формул (5.10) и (5.11) видно, что в рассматриваемом магнитном поле на каждый цилиндрический элемент жидкости единичной массы действует сила, содержащая стационарную компоненту F_мо и нестационарную компоненту F_м1:

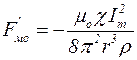; (5.12)

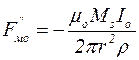; (5.13)

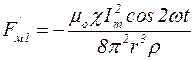; (5.14)

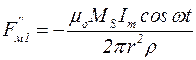. (5.15)

Действие стационарной силы на жидкость при фиксированных цилиндрических границах может привести лишь к некоторому распределению статического давления. Если абсолютное значение этого давления не слишком велико, оно не окажет существенного влияния на характер колебательного движения, и составляющие 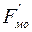и 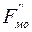можно вообще исключить из дальнейшего рассмотрения. Составляющие 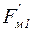и 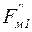следует рассматривать как вынуждающую силу, причем знак минус целесообразно отбросить, что равносильно изменению начальной фазы на p.

В дальнейшем с целью упрощения расчетов рассматривается случай «тонких» цилиндрических слоев, для которых выполняется неравенство

h/r<<1, (5.16)

где hºr₁-r_o – толщина слоя.

Принимая во внимание монотонность зависимосте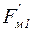й и 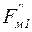от r и малость рассматриваемого интервала изменения r, заменим выражения (5.10) и (5.11) их средним значением в интервале r₁-r_o:

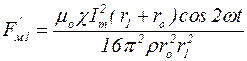; (5.17)

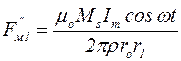. (5.18)

Усреднение (5.14) и (5.15) позволяет воспользоваться для решения дифференциального уравнения (5.12) специальными функциями.

Подставляя последовательно (5.17) и (5.14) в правую часть (5.2), получим два дифференциальных уравнения, имеющих общий вид

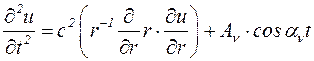. (5.19)

Для реализации случая 1 или случая 2 в уравнении (5.15) необходимо принять соответственно

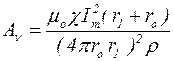и a_n=2w, (5.20)

или

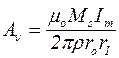и a_n=w. (5.21)

Решение дифференциального уравнения (5.19) выполнено путем разделения переменных r и t, для чего u(r,t) представлено в виде:

u=U(r) ×cosa_nt. (5.22)

После подстановки (5.22) в (5.19) и выполнения простейших преобразований получим новое дифференциальное уравнение:

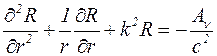, (5.23)

где k=k₁=2w/c для случая 1 и k=k₂=w/c для случая 2.

Дифференциальное уравнение (5.23) является неоднородным, а решение соответствующего однородного уравнения хорошо известно - оно выражается через бесселевы функции нулевого порядка:

R^*= a_oJ_o(kr) + b_oN_o(kr), (5.24)

где J_o – функция Бесселя нулевого порядка;

N_o – функция Неймана нулевого порядка;

a_o и b_o – произвольные постоянные величины.

Чтобы получить общее решение неоднородного уравнения (5.23), к решению (5.24) следует добавить постоянную величину A_n/c²k²:

R^*= a_oJ_o(kr)+b_oN_o(kr)=-A_n/c²k². (5.25)

Как будет показано ниже, наибольшее значение длины резонансной звуковой волны l составляет 2h. Отсюда на основании (5.16) kr>>1 и, следовательно, бесселевы функции можно заменить асимптотическими выражениями

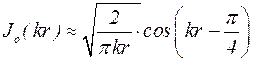; (5.26)

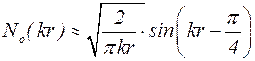, (5.27)

с учетом, которых решение (5.24) принимает вид

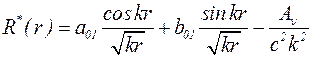. (5.28)

Значения постоянных a_o1 и b_o1 определим из граничных условий R^*(r₀)=0 и R^*(r₁)=0, поскольку ограничивающие цилиндры считаются абсолютно жесткими:

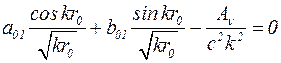; (5.29)

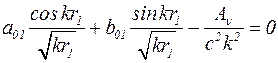. (5.30)

Из системы уравнений (5.29) и (5.30) получено:

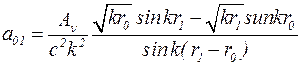; (5.31)

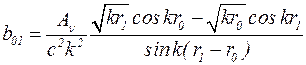. (5.32)

Подставляя a_o1 и b_o1 в (5.28) и полученное в результате этого выражение в (5.22), найдем решения дифференциального уравнения (5.19) применительно к случаю 1 и случаю 2:

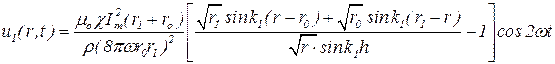(5.33)

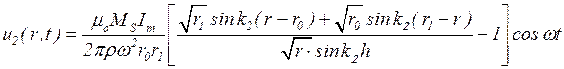. (5.34)

Анализ выражений (5.33) и (5.34), описывающих движение частиц жидкости, показывает, что частицы в условиях данной модели совершают радиальные гармонические колебания с круговой частотой 2w в случае 1 и w в случае 2. Амплитуда колебаний зависит от магнитных параметров МЖ – магнитной восприимчивости c в случае 1 и – намагниченности насыщения М_S в случае 2. Если c=0 или М_S=0, что справедливо для обычных немагнитных жидкостей, то колебаний не возникает. МЖ из огромного количества разнообразных жидких сред, не считая жидкие металлы, характеризуемые высокой электропроводностью, обладают уникальным свойством преобразования энергии электромагнитных колебаний в энергию упругих механических колебаний.

Нетрудно видеть, что при w=w_m=pcm/2h (в случае 1) и w=w_m=pcm/h (в случае 2), где m=1, 2, 3…, знаменатель выражения в квадратных скобках формул (5.33) и (5.34) обращается в нуль, а амплитуда колебаний принимает бесконечно большое значение. Следовательно, при частотах переменного тока w=w_m колебания становятся резонансными. Получение бесконечно больших амплитуд колебаний при резонансе является следствием сделанного предположения об отсутствии диссипации энергии в среде и отсутствия излучения звука в ограничивающие цилиндры.

Рассмотрим конкретный пример. Пусть h=5 мм при r_o=50 мм. Поскольку при резонансе h=ml/2, то длина волны основной резонансной частоты будет равна 10 мм. Принимая для МЖ с=1300 м/с, получим значение основной резонансной частоты n=с/l=130 кГц; реализация ее в случае 1 и в случае 2 достигается применением переменного тока с частотой, соответственно равной 130 и 65 кГц.

Таким образом, описанная методика в принципе может быть использована для непосредственного возбуждения резонансных ультразвуковых колебаний в МЖ. В дальнейшем МЖИ с той же геометрией магнитного поля был рассмотрен в работе Р. Dubbeldaу (1980 г.). Им отмечено, что цилиндрическая модель наиболее полно использует свойства жидкого магнитного материала, и делается вывод о ее применимости также в области звуковых частот 100 – 3000 Гц. Оба поля – постоянное и возбуждающее – имеют азимутальную геометрию и зависят только от радиального расстояния, причем поля создаются токами, текущими по проводникам, намотанным в азимутальном направлении.