Поляризация при отражении и преломлении на границе раздела двух сред
Формальная теория отражения и преломления света строится на основе граничных условий, которым удовлетворяют векторы электромагнитного поля на границе двух сред. Она определяет величины, характеризующие отраженную и преломленную волны, но ничего не говорит о механизме возникновения этих волн.
Граничные условия состоят в том, что на границе раздела (в отсутствии поверхностных зарядов и токов) должны быть непрерывны тангенциальные составляющие векторов 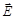 ,
, 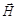 и нормальные составляющие векторов
и нормальные составляющие векторов 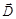 ,
,  .
.
Все эти условия являются следствием макроскопических уравнений Максвелла в интегральной форме, а потому верны для всяких сред, пока последние можно рассматривать как сплошные. Используя граничные условия, в 1821 году Огюстен Жан Френель (1788–1827) получил выражения для комплексных амплитуд преломленной и отраженной волн. Приведем данные уравнения без вывода.
Представим каждую из трех волн (падающую, преломленную, отраженную) в виде наложения двух некогерентных волн, в одной из которых колебания совершаются в плоскости падения луча, а в другой – перпендикулярно этой плоскости. Комплексную амплитуду первой будем обозначать символом ²t², второй – символом ²n². Падающую, преломленную и отраженную волны обозначим индексами ²пад², ²пр²,
²отр ², соответственно. Тогда формулы Френеля запишутся в виде
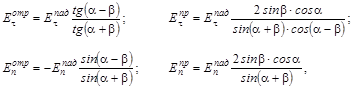 (5.3.1)
(5.3.1)
где a – угол падения, b – угол преломления.
 Формулы (5.3.1) устанавливают соотношения между комплексными амплитудами падающей преломленной и отраженной волн в точке падения луча на границу раздела двух диэлектриков. Если падающая волна была линейно поляризована, то отраженная и преломленная волны будут также линейно поляризованы. При нормальном падении луча исчезает различие между волнами, поляризованными в плоскости падения и перпендикулярно ей.
Формулы (5.3.1) устанавливают соотношения между комплексными амплитудами падающей преломленной и отраженной волн в точке падения луча на границу раздела двух диэлектриков. Если падающая волна была линейно поляризована, то отраженная и преломленная волны будут также линейно поляризованы. При нормальном падении луча исчезает различие между волнами, поляризованными в плоскости падения и перпендикулярно ей.
Если n1 < n2, т.е. a > b, то нормальная составляющая амплитуды отраженной волны меняет знак по сравнению соответствующей амплитудой падающей волны или 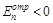 . Это означает, что отражение сопровождается скачкообразным изменением фазы на p. Если n1 > n2, т.е. a < b, то
. Это означает, что отражение сопровождается скачкообразным изменением фазы на p. Если n1 > n2, т.е. a < b, то  – изменения фазы не происходит.
– изменения фазы не происходит.
При скользящем падении, когда a стремится к 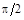 ,
, 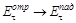 и
и  , тогда как
, тогда как  и
и 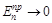 . Таким образом, почти вся энергия, падающая на границу раздела, отражается от нее.
. Таким образом, почти вся энергия, падающая на границу раздела, отражается от нее.
Как видно из формул (5.3.1), 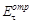 никогда не обращается в ноль. Исключением является случай, когда
никогда не обращается в ноль. Исключением является случай, когда 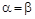 , т.е. n1 = n2. Напротив, при
, т.е. n1 = n2. Напротив, при 
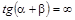 , т.е.
, т.е. 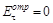 . Таким образом, если линейно поляризованная волна падает так, что вектор
. Таким образом, если линейно поляризованная волна падает так, что вектор 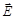 лежит в плоскости падения луча, то при некотором угле падения света отраженная волна исчезает. В этом состоит закон Брюстера. Соответствующий угол aБр называется углом Брюстера. Так как с одной стороны
лежит в плоскости падения луча, то при некотором угле падения света отраженная волна исчезает. В этом состоит закон Брюстера. Соответствующий угол aБр называется углом Брюстера. Так как с одной стороны  , а с
, а с
другой, из закона преломления  , то
, то
 .
.
Таким образом,
 . (5.3.2)
. (5.3.2)
Если неполяризованный свет падает под углом Брюстера, то отраженный свет будет линейно поляризован в плоскости, перпендикулярной плоскости падения луча. Степень поляризации преломленного луча максимальна, однако он поляризован только частично. Если угол падения света отличен от 0 и от aБр, то отраженный и преломленный лучи поляризованы частично. В отраженном луче преобладают колебания, перпендикулярные плоскости падения, в преломленном – преобладают колебания, параллельные плоскости падения луча.
 С точки зрения атомистической теории строения вещества любую среду можно рассматривать как вакуум, в который вкраплены частички вещества (атомы). Под действием падающей волны внутри каждого атома возбуждаются колебания электронов, вследствие чего атомы становятся источниками вторичных волн. Эти волны распространяются между частицами со скоростью света. Возбужденные одной и той же волной вторичные волны являются когерентными и могут интерферировать. Именно интерферирующие вторичные волны дают преломленную и отраженную волну. Колеблющиеся электроны можно представить как линейные гармонические осцилляторы. Вероятность излучения осциллятором волны в направлении его колебаний равна нулю, тогда как наиболее вероятным направлением распространения является направление, перпендикулярное направлению колебаний. Вероятность излучения осциллятора изображают на диаграмме. Эта диаграмма строится так: длина отрезка ОА пропорциональна интенсивности излучения в направлении луча, определяемом углом J.
С точки зрения атомистической теории строения вещества любую среду можно рассматривать как вакуум, в который вкраплены частички вещества (атомы). Под действием падающей волны внутри каждого атома возбуждаются колебания электронов, вследствие чего атомы становятся источниками вторичных волн. Эти волны распространяются между частицами со скоростью света. Возбужденные одной и той же волной вторичные волны являются когерентными и могут интерферировать. Именно интерферирующие вторичные волны дают преломленную и отраженную волну. Колеблющиеся электроны можно представить как линейные гармонические осцилляторы. Вероятность излучения осциллятором волны в направлении его колебаний равна нулю, тогда как наиболее вероятным направлением распространения является направление, перпендикулярное направлению колебаний. Вероятность излучения осциллятора изображают на диаграмме. Эта диаграмма строится так: длина отрезка ОА пропорциональна интенсивности излучения в направлении луча, определяемом углом J.
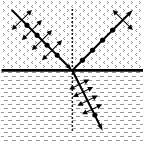
Представим неполяризованную волну, падающую на границу раздела, в виде суперпозиции колебаний, параллельных плоскости падения луча (изображены точками) и перпендикулярно ей (изображены стрелочками). Рассмотрим действие каждой составляющей в отдельности. Первая возбуждает колебания электронов в плоскости падения луча. Следовательно, вторичные волны, имеющие такую ориентацию вектора напряженности, с большей вероятностью можно обнаружить в преломленном луче. Когда свет падает на границу раздела под углом Брюстера, тогда, как отмечалось ранее, угол между отраженным и преломленным лучами равен p/2. Это означает, что колебания электронов должны происходить в направлении отраженного луча. Следовательно, вероятность обнаружения вторичных волн, поляризованных в плоскости падения луча, становится равной нулю. Вторая составляющая возбуждает колебания электронов в плоскости, совпадающей с плоскостью границы раздела сред. Волны, поляризованные в этой плоскости, присутствуют как в отраженном, так и в преломленном свете.
