Рациональные сечения при изгибе

Определим рациональные сечения при изгибе, для этого срав­ним моменты сопротивления простейших сечений.

Осевой момент инерции прямоугольника (рис. 32.4, вывод формулы в лекции 25) ра­вен

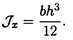
Осевой момент сопротивления прямоуголь­ника

Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).

Вариант на рис. 32.5, б обладает большим сопротивлением изгибу при прочих равных условиях.

Осевой момент инерции круга (рис. 32.6) равен

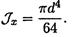
Осевой момент сопротивления круга

Все необходимые расчетные данные (площади, моменты инер­ции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1).

Для материалов, одинаково работающих на растяжение и сжа­тие, выбирают сечения, симметричные относительно оси, вокруг ко­торой совершается изгиб (рис. 32.7).

Пример

Сравним моменты сопротивления двух сечений одинаковой пло­щади: двутавра (рис. 32.7г) и круга (рис. 32.7а).

Двутавр № 10 имеет площадь 12 см², осевой момент инерции 198см⁴, момент сопротивления 39,7см³.

Круг той же площади имеет диаметр осевой

момент инерции J_x = 25,12см⁴, момент сопротивления W_x = 6,2см³.

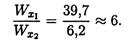
Сопротивление изгибу у двутавровой балки в шесть раз выше, чем у балки круглого сечения.

Из этого примера можно сделать вывод: сечения прямо­угольные, квадратные, круглые и ромбовидные нерациональны (рис. 32.7а, б).

Для материалов, обладающих разной прочностью при растяже­нии и сжатии (хрупкие материалы обладают значительно большей прочностью на сжатие, чем на растяжение), выбирают асимметрич­ные сечения тавр, рельс и др.

Расчет, на прочность при изгибе

Рассчитать на прочность — это значит определить напряжение и сравнить его с допустимым.

Условие прочности при изгибе:

где [σ_иJ — допускаемое напряжение.

По этому неравенству проводят проверочные расчеты после окончания конструирования балки.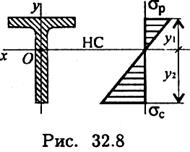

Для балок из хрупких материалов расчеты ведут по растянутой и сжатой зоне одновременно (рис. 32.8).

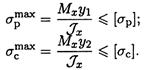
При проектировочном расчете определя­ют потребные размеры поперечных сечений балки или подбирают материал.

Схема нагружения и действующие нагрузки известны.

По условию прочности можно определить нагрузочную способ­ность балки [М_и] = W_x [сг].

Примеры решения задач

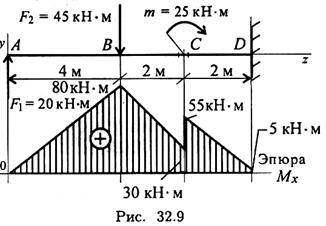
Пример 1. Подобрать размеры сечения балки в виде двутавра. Известна схема нагружения балки (рис. 32.9), материал — сталь, допускаемое напряжение материала при изгибе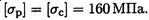

Решение

1. Для защемленной балки реакции в опоре определять не следует.

Проводим расчеты по характерным точкам. Размеры сечения подбираем из расчета по нормаль­ным напряжениям. Эпюру поперечных сил строить необязательно.

Определяем моменты в характерных точках.

М_А = 0; М_В = F₁• 4; М_в = 20 • 4 = 80 кН • м.

В точке С приложен внешний момент пары, поэтому расчет про­водим для левого сечения (без момента) и для правого — с момен­том т.

Выбираем соответствующий масштаб по максимальному значе­нию изгибающего момента. Опасное сечение — сечение балки, где действует максимальный момент. Подбираем размеры балки в опасном сечении по условию прочности

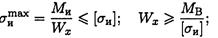
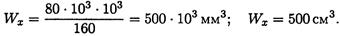
Основываясь на значении W_x = 500 см³ по таблице ГОСТ 8239-89 выбираем двутавр № 30а: момент сопротивления W_x = 518 см³; площадь сечения А = 49,9 см².

Для сравнения рассчитаем размеры балки квадратного сечения (рис. 32.10) при том же моменте сопротивления сече­ния.

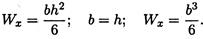
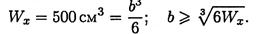
Сторона квадрата Площадь сечения бал­ки А = b² = 14,5² = 210,2 см².

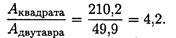
Балка квадратного сечения в 4 раза тяжелее.

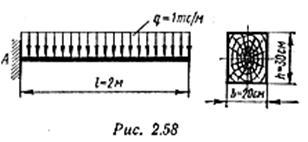
Пример 2. Проверить прочность деревянной балки (рис. 2.58), если[σ] = 100 кгс/см²; [т] = 10кгс/см².

Решение

Максимальные изгибающий момент и попе­речная сила возникают в сечении заделки.

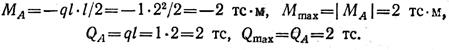
Максимальные нормальные напряжения

т. е. прочность по нормальным напряжениям обеспечена.

Максимальные касательные напряжения

следовательно, и по касательным напряжения прочность обеспечена.

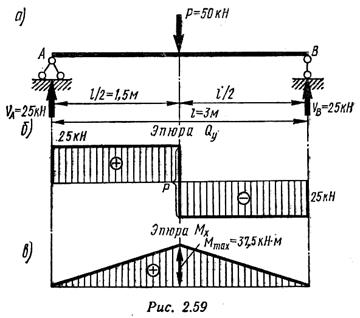
Пример 3. Подобрать сечение стальной балки, изображенной на рис. 2.59, а в трех вариантах: 1) про­катный двутавр, 2) прямоугольник с отношением сторон h/b = 4/3, 3) круг. Определить отношения масс балок пря­моугольного и круглого сечения к массе балки двутавро­вого сечения. Допускаемое напряжение [σ] = 160 Н/мм². Проверить подобранные сечения по касательным напряже­ниям. Допускаемое касательное напряжение [т] = 96 Н/мм².

Решение

Эпюры поперечных сил и изгибающих момен­тов построены на рис. 2.59,6, в.

Максимальный изгибающий момент возникает в сече­нии посередине пролета балки М_хтах= 37,5 кН-м. Тре­буемый момент сопротивления

Подбираем сечение балки в трех вариантах:

— Сечение — прокатный двутавр. По таблице ГОСТ 8239—72 подходит двутавровый профиль № 20а, его момент сопротивления W_x = 237 см³, площадь сечения F₁ = 35,5 см²,

— Сечение — прямоугольник с отношением сторон h/b = 4/3.

Для прямоугольника W_x = bh²/6; подставляя сюда b = 3h/4 и приравнивая требуемому значению, получаем:

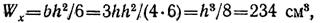
откуда

Площадь сечения F₂ = 12,3_*9,2 = 113 см².

— Сечение — круг.

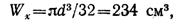
откуда

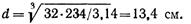
Площадь поперечного сечения

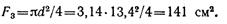
Отношение масс (равное отношению площадей сечений)

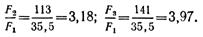
Следовательно, балка прямоугольного сечения тяжелее двутавровой в 3,18 раза, а балка круглого сечения — в 3,97 раза.

Проверим прочность балки по касательным напряже­ниям.

Наибольшая поперечная сила

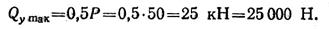
Для двутавра № 20а из ГОСТ 8239—72 находим J_х/S_x = 172 мм, толщина стенки балки b = 0,7 см = 7 мм. Наибольшие касательные напряжения для двутавра

Для прямоугольного сечения h = 123 мм, b = 92 мм

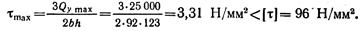
Для круглого сечения d = 134 мм

Во всех случаях максимальные касательные напряже­ния оказались значительно ниже допускаемых.

Пример 4. Определить, какую наибольшую рав­номерно распределенную нагрузку q можно приложить к двухопорной балке пролетом l = 2 м, если ее сечение представляет круг d = 220 мм, а допускаемое напряжение [σ] =100 Н/мм².

Решение

Для данного случая наибольший изгибаю­щий момент возникает посередине пролета

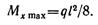
Определяем допускаемое значение наибольшего изги­бающего момента

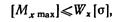
где

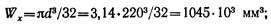
Тогда

Приравниваем вычисленное значение допускаемого изги­бающего момента его значению, выраженному через на­грузку:

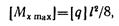
откуда

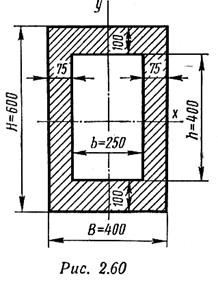Пример 5.Определить допускаемый изгибающий момент для чугунной балки, сечение которой изображено на рис. 2.60. Допускаемые напряжения на растяжение [σ_р]=300 кгс/см², на сжатие [σ_с] = 800 кгс/см².

Решение

Момент инерции сечения вычисляем как раз­ность моментов инерции большого и малого прямоуголь­ников

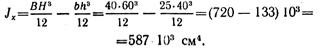
Осевоймомент сопротивления

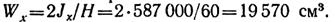
Допускаемый изгибающий момент определяем из расчета по наибольшим растягивающим напряжениям

то же, по наибольшим сжимаю­щим напряжениям

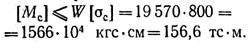
Меньший из вычисленных моментов [М_р] = 58,7 тс-м опре­деляет допускаемую нагрузку балки.

Таким образом, в чугунной балке симметричного сече­ния допускаемая нагрузка ограничивается прочностью растянутых волокон. Чтобы для чугунной балки допускае­мая нагрузка была одинакова по условиям прочности растянутых и сжатых волокон, сечение ее должно быть несимметричным относительно нейтральной оси. Расстоя­ния от нейтральной оси до крайних волокон растянутой зоны у_р и сжатой у_с должны удовлетворять отношению

Этого можно добиться, в частности, применив несимметричный двутавр, у которого горизонтальная полка, находящаяся в растянутой зоне, толще, чем полка, расположенная в сжатой зоне.

Контрольные вопросы и задания

1. Напишите формулу для определения нормального напряже­ния при изгибе в любой точке поперечного сечения.

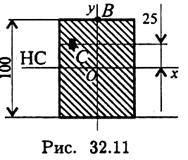
2. Нормальное напряжение в точке В поперечного сечения 120МПа. Определите напряжение в точке С (рис. 32.11).

3. В каком случае (рис. 32.12) балка выдержит большую нагрузку?

4. Напишите формулы для определения момента инерции и мо­мента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин.

5. Напишите условие прочности при изгибе.

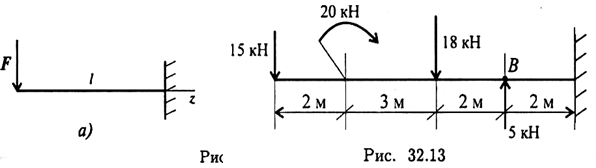
6. Определите изгибающий момент в точке В (рис. 32.13), ис­пользуя метод характерных точек.

7. Подберите размеры поперечного сечения балки в виде швел­лера. Максимальный изгибающий момент 15кН-м; допускаемое на­пряжение материала балки 160 МПа.

ЛЕКЦИЯ 33