Уравнения Навье-Стокса, уравнение энергии, уравнения переноса компонент смеси

Какая математика используется программами, реализующими методы вычислительной гидродинамики?

·Дифференциальные уравнения основных процессов представляют собой мат. формулировку законов сохранения.

Входящие в уравнения переменные представляют собой удельные величины, т.е. величины, отнесенные к единице объема или массы (например, плотность, концентрация, энергия, энтальпия).

·Дивергенция

Пусть J – поток некоторой величины Ф;

Ф={u, v, w, Y_n, h) – функция Ф может принимать значение любой из функций, указанных в скобках.

,

,

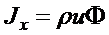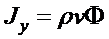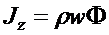
V = (iu+jv+kw)

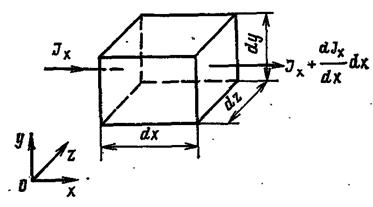
Рис.2. Баланс потоков через контрольный объем.

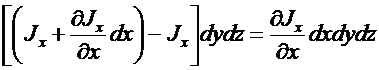
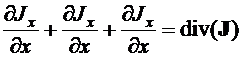
· Для стационарного процесса в отсутствие источников div(J) = 0,

Если величина Ф меняется во времени, то изменение потока

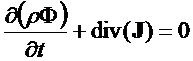(2.1)

Производная по времени описывает скорость изменения свойства Ф в единицу времени.

Если в объеме есть источники, то

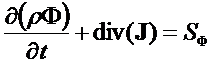(2.2)

Закон сохранения концентрации химической компоненты

Пусть Ф=Y_n – массовая концентрация компоненты n,

J=rVY_n+Г_n, где Г_n – диффузионный поток компоненты n.

Согласно закону Фика

Г_n = -D_ngrad(Y_n) =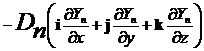

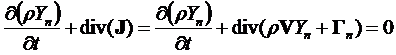
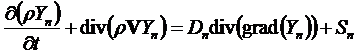
Уравнение энергии

· будем полагать, что скорость течения мала, подвод тепла от трения пренебрежимо мал, l = Const, C_p = Const.

Ф=h – удельная энтальпия, h=C_pT

J=rVh-l×grad(T)

l – коэффициент теплопроводности

подставляя Ф и J в уравнение (2.1) получим

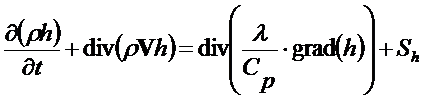
Таким образом, мы можем записать общий вид дифференциального уравнения

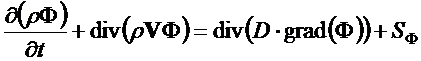
Это уравнение записано в векторной форме;

В тензорной форме это уравнение имеет вид

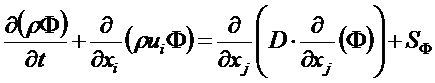
Это сокращенная форма записи; в декартовых координатах i=1,2,3, j=1, 2, 3. Если индекс повторяется, то это означает суммирование, например,

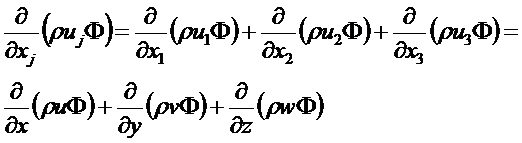
Уравнение неразрывности в принятых обозначениях запишется

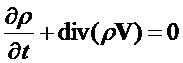
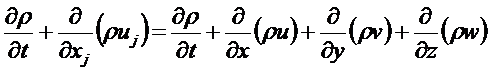
Диффузионная часть потока в тензорной форме запишется:

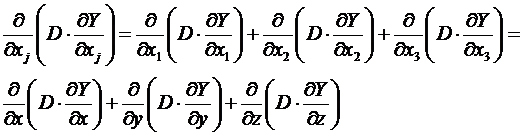
Уравнения газовой динамики (уравнения Навье-Стокса). Тензорная запись уравнений Навье-Стокса.

Мы запишем систему уравнений для решения задач газовой динамики в упрощенном виде. Во-первых, для несжимаемой жидкости, во-вторых, для плоского (2D) течения. Выглядит эта система так

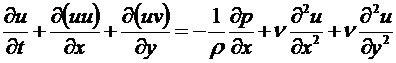
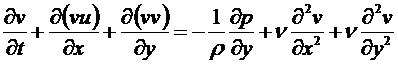
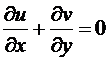
Первые два уравнения – это уравнения движения в проекции на координатные оси, третье уравнение – уравнение неразрывности.

Напомню о тензорной записи этой системы. Тензорная запись получается короче, поэтому мы будем ее использовать.

Будем обозначать координатные оси х₁, х₂, х₃;

компоненты вектора скорости u₁, u₂, u₃;

Тогда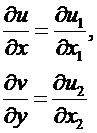

и т.д.

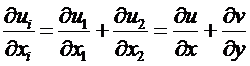
Таким образом, уравнение неразрывности мы можем записать

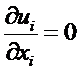
При записи уравнении движения будем использовать 2 индекса, первый индекс относится к оси, в проекции на которую записано уравнение, а второй – изменяется в соответствии с компонентой вектора скорости. Два уравнения мы запишем, таким образом, как одно.

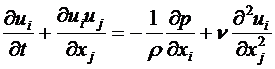
(Расшифровка записи).

Как решать эту систему уравнений?