Графики элементарных функций и их свойства

Свойства функции

Определить свойства функций и заполнить таблицу:

1. Область определения
2. Множество значений
3. Нули функции
4. Четность, нечетность
5. Периодичность
6. Монотонность
7. Экстремумы

Функция, её график	Свойства функции
Линейная функция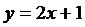
Степенная функция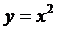
Степенная функция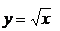
Показательная функция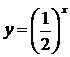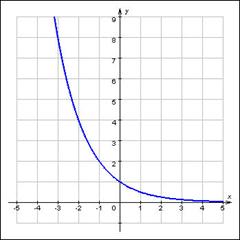
Логарифмическая функция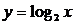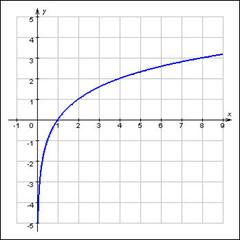
Тригонометрическая функция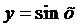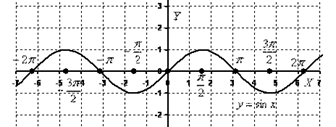
Тригонометрическая функция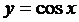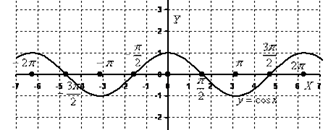
Тригонометрическая функция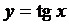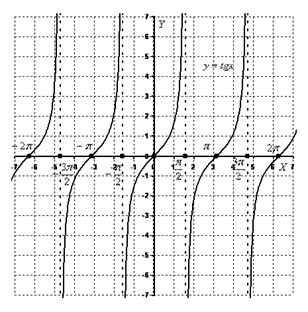
Тригонометрическая функция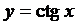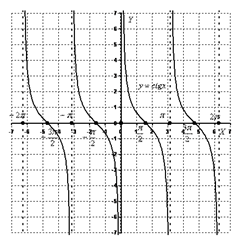

Вычисление производных рациональных и сложных функций.

Найти производные заданных функций:

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

л) y=

м)

н)

о)

п)

р)

с)

т)

у)

ф)

х)

ц)

ч)

ш)

Найти производные высших порядков:

1)y = sin 3x; n = 101

2)y = ln(1 + x); n = 1010

3). y = 23x;

4) y = sin2 x; n = 103

5). y = cos2 x; n = 110

6). y = (4x + 1)

7) y = xcosx, n = 10

Дифференциал функции

Найти дифференциалы функции:

а) f(x) = 2 - 3x + x3

б) f(t) = t2 + cos3t – 5

в)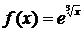

Исследование функций при помощи производных

Алгоритм исследования функции:

Какие точки называются точками разрыва?

Какие точки являются точками разрыва первого рода?

Какие точки являются точками разрыва второго рода?

Классифицировать точки разрыва:

Что такое асимптота?

Функция имеет асимптоты:(перечислить)

Как найти вертикальную асимптоту

Как найти наклонную асимптоту?

Когда функция имеет горизонтальную асимптоту?

Как найти экстремумы функции?

Как найти точки перегиба функции?

Какие функции являются периодическими?

Как определить четность и нечетность функции?

Как вычислить точки пересечения функции с осями координат?

Тема 1. 2 Интегральное исчисление

Составить таблицу неопределенных интегралов:

ТАБЛИЦА

Методы интегрирования

Перечислить методы интегрирования

Найдите неопределенные интегралы, приводя их к каноническому виду:

1.	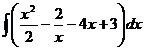5.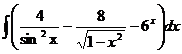
2.	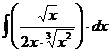6.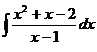
3.	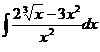7.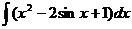
4.	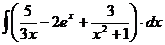8.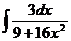

Найдите неопределенные интегралы методом подстановки или подведением под знак дифференциала:

1.	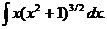6.	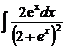11.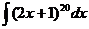
2.	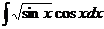7.	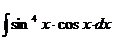12.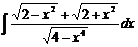
3.	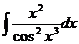8.	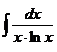13.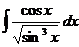
4.	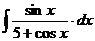9.	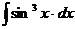14.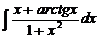
5.	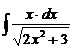10.	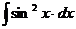15.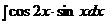

Интегралы, вычисленные методом подстановки:

Интегралы, вычисленные методом подведения под знак дифференциала:

Найдите неопределенные интегралы методом интегрирования по частям:

1.	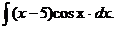6.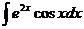
2.	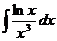7.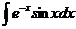
3.	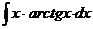8.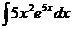
4.	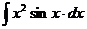9.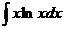
5.	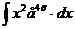10.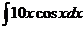

Определенный интеграл. Риложения определенного интеграла.

Напишите формулу Ньютона – Лейбница:

Методы вычисления определенных интегралов

1) Метод непосредственного интегрирования

Найдите определенные интегралы методом непосредственного интегрирования:

1.

2.

3.

2) Метод подстановки

Найдите определенные интегралы методом подстановки:

1.

2.

3.

3) Метод интегрирования по частям

Найдите определенные интегралы методом интегрирования по частям:

1.

2.

Приложения определенного интеграла

Найти площадь фигуры, ограниченной линиями и сделать эскиз площади, полученной фигуры:

а)

б) y = x, y = x², x = 2

Найти объем тела, полученного вращением

а) вокруг оси Ох криволинейной трапеции, ограниченной гиперболой , прямыми х = 1, х = 4 и осью Ох

б) вокруг оси Оу криволинейной трапеции, ограниченной линиями х² = 4у, у = 4, х = 0.

РАЗДЕЛ 2. ЛИНЕЙНАЯ АЛГЕБРА