Четыре арифметических операции

· Сложение. К концу года класс должен с легкостью складывать двузначное число и однозначное (например, 57 + 6).

· Вычитание. К концу года класс должен с легкостью вычитать однозначное число из двузначного (например, 52 – 6), а также двузначное из двузначного, если ответом будет однозначное число (например, 72 – 69).

· Ученики должны приобрести более глубокое понимание понятий умножения и деления, например:
3 х 2 = __ спросите: «Сколько будет три раза по 2?»
12 : 3 = __ спросите: «Сколько раз три помещается в двенадцати?»

· К концу года дети должны уметь выполнять все четыре операции (и обратные к ним, на той же странице) и знать разницу между ними. (Задачи пока не должны быть сложными).

· Введение сложения и вычитания в столбик будет сделано в третьем классе. Вся письменная работа с вычислениями совершается в строчку (например, 9=5+4, 5+4=9).

· Ориентация во времени.

Дети должны знать дни недели и месяцы года. Понятия «завтра» и «вчера» должны постоянно использоваться.

Чудеса чисел

Мир чисел должен быть наполнен чудесами и вызывать восхищение. Один из способов показать это – рисовать геометрические фигуры, отображающие отношение таблицы умножения и круга, разделенного на 10 или 12 частей.

Уроки и темы для второго класса

Расписание

В расписании снова стоит 12 недель математики. Первая эпоха должна проходить где-то в октябре, вторая в январе, а третья весной. Каждая эпоха длится 4 недели, а в конце года проводится неделя повторения.

Не забудьте!

· Каждый день мы вспоминаем предыдущий урок.

· Каждый день мы даем детям что-то новое.

· Каждый день ученики отрабатывают новый материал и некоторые другие темы на выбор учителя.

Повторение пройденного материала

· Большинство указанных ниже тем были введены ранее. Для того, чтобы дети хорошо усвоили материал, его нужно систематически повторять. Очевидно, что мы не можем каждый день повторять все темы. Учителю нужно решить, какие из тем нужно повторять каждый день, даже во время других эпох. Обратите внимание, что эта работа не должна занимать более 10 минут в день.

Мир чисел

· Счет в пределах 100 – свободно, в пределах 1000 – без затруднений (вперед и назад). Дети должны уверенно считать без всякой помощи.

· Числовые диктанты. Числовые диктанты помогают детям осваивать большие числа, которые появились при знакомстве с разрядами. Диктанты продолжаются и после того, как работа с разрядами закончена. Ученики должны уверенно писать числа от 1 до 1000.

· Язык. Обратите внимание на правильное произнесение названий больших чисел.

Таблица сложения и вычитания

· Помните, что таблица умножения/деления это тема номер один для второго класса.

· К концу года класс должен уверенно работать с каждым рядом таблицы от 1 до 12. Это потребует ежедневной систематической работы!

· Табличными умножением и делением занимаются одновременно. Дети должны получить переживания того, как связаны умножение и деление.

Работа с четырьмя арифметическими операциями

Ученики продолжают ежедневно отрабатывать вычислительные навыки, а также формируют стратегии вычислений. Дети должны решать довольно много примеров, чтобы почувствовать уверенность в этой деятельности. Постарайтесь придумывать интересные задания. Например, можно предложить провести серию вычислений, так чтобы ответы образовали некую последовательность:

18 + 17 = 35
21 + 14 = 35
29 + 6 = 35
А затем появляется «сюрприз» - другой ответ!
16 + 18 = 34

Время

Мы рассматриваем названия дней недели, месяцев и времен года на главном уроке, а потом время от времени коротко возвращаемся к этой теме, чтобы ученики могли свободно пользоваться этими понятиями.

Устный счет

· Проводите устный счет ежедневно (10 минут или меньше).

· Устный счет помогает детям освоится с четырьмя операциями.

· Примеры вычислений: 28+5, 14:2, 8х5, 86-3, 76-74, 42-6, 72-69.

· Нахождение середины. Сначала такие задания должны быть легкими и становиться все сложнее в следующих классах. Примеры:
Какое число находится посередине между 25 и 29?
Какое число находится посередине между 5 и 13?
Какое число находится посередине между 5 и 23?
Какое число находится посередине между 25 и 31?

Текстовые задачи

Во втором классе задачи должны представлять собой образные истории. Более простые задачи решаются на устном счете. Вот несколько примеров:

· В пустой автобус сели 8 пассажиров. На следующей остановке 3 человека вышли, и 4 вошли. Сколько человек поедет дальше?

· Мама и двое детей пошли в магазин. Они купили 24 апельсина. Апельсины выглядели так аппетитно, что все трое съели по одному апельсину. По пути домой дети встретили друга, и вместе с ним дети съели по одному апельсину. Сколько апельсинов оказалось в сумке у мамы, когда они пришли домой?

· Папа работал осенью в саду. В дупле на дереве он нашел 5 орехов, 6 он нашел зарытыми на земле, а еще 8 – на полке в сарае. Сколько всего орехов нашел папа?

Тетрадь для упражнений

Во втором классе хорошо завести тетрадь для упражнений. Все, что подделывается во время двигательных упражнений, может быть записано в тетрадь. Такая тетрадь помогает детям научиться организовывать свою работу. Конечно, все записи в тетради должны быть сделаны аккуратно.

Эпоха 1: Разряды и таблица умножения

Новый материал и содержание эпохи

· Таблица умножения

o На первой эпохе математики во втором классе мы продолжаем заниматься таблицей умножения.

o Помните, что нашей целью является, чтобы к концу года класс уверенно себя чувствовал со всеми рядами таблицы умножения от 1 до 12. Это требует ежедневной систематической работы и тщательного планирования.

· Разряды

o Гномы и сокровища. Мы можем придумать историю о гномах, добывающих драгоценные камни. Они придумывают, как вести учет камням, как их считать. Очень хорошо, если дети сначала попытаются придумать свою систему для этого. Можно воспользоваться такой идеей: кучки по 10 камней кладутся в мешочки, кучки из 10 мешочков кладутся в маленькие корзинки, 10 корзинок помещаются в тележку на колесах и т.д. Таким образом, число 3785 будет представлено тремя тележками, семью корзинками, восемью мешочками и пятью отдельными камнями. Эту историю можно проиллюстрировать в тетрадях для главного урока. Из нее можно далее развить другую исторю, возможно, не столь подробную…

o Лесопилка. У дровосека есть лесопилка, которая производит доски на продажу. Из досок делают связки по 10 штук в каждой. 10 связок укладывают в ящики, 10 ящиков составляют один вагон. Таким образом, число 2497 будет представлено двумя вагонами, четырьмя ящиками, девятью связками и семью отдельными досками. Эта история хороша для изучения разрядов. Дети могут использовать для нее палочки от мороженого. Дайте детям побольше палочек, около 2400, и попросите их разложить палочки, как это сделал дровосек, чтобы потом можно было легко сосчитать.

· Четыре арифметических операции. Работайте над стратегиями сложения и вычитания. Дети должны свободно складывать в пределах 24, и с легкостью в пределах 100. Эта работа продолжается весь год.

Движение

· Счет с шагами. Возьмите любое числа между 100 и 1000 и попросите класс считать перед и назад. Далее перейдите к работе в малых группах и индивидуальной.

· Хлопки и топанье. Ритмически прорабатывайте таблицу умножения с хлопками и топаньем. Например, для ряда на 4: четыре (хлопаем в ладоши) это (хлопаем по коленям) один (хлопаем в ладоши) раз (руки скрещены) четыре (хлопаем в ладоши). Для такой работы вы можете придумать очень много различных вариантов.

· Двенадцатичастный круг. Каждый ряд таблицы умножение можно вывести из двенадцатичастного круга. Мы хотим показать именно круг из двенадцати частей, так как он представляет космическую реальность. Дети в этом возрасте все еще сильно связаны с космосом, миром из которого они пришли. Дети знают этот круг на примере часов, им знакомы также 12 месяцев (вторая эпоха). Мы можем проводить эту работу для каждого ряда таблицы умножения (начиная с 2). Например, возьмем ряд на 5. Дети сидят в кругу на стульях, обозначающих числа на часах. Один ребенок берет клубок ниток и встает в центр круга. Ученик, сидящий на стуле, обозначающем 12 (а также 0) держит конец нити. Ребенок с клубком делает пять шагов и приходит к числу 5. Номер 5 берет нить, и все говорят: «Пять это один раз по пять.» Таким образом, ребенок в центре проходит все числа из таблицы умножения на пять вплоть до 60=12х5. Клубок обходит круг несколько раз. Когда процесс закончен, оказывается, что мы вместе связали чудную 12-конечную звезду.

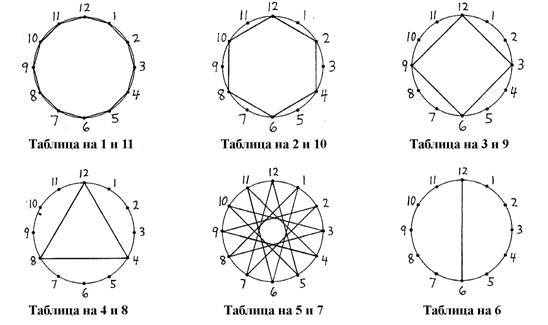
· Десятичастный круг.

o Только что описанный процесс можно провести и для 10-частного круга. В этом случае, мы начинаем с десяти стульев, каждый из которых обозначает числа он 0 до 9. Геометрическая фигура строится в соответствии с количеством единиц в числах из определенного ряда таблицы.

o Например, для таблицы на 4 нитка проходит от 4 (4=1х4) к 8 (8=2х4), к 2 (так как на третьем шаге 12=3х4, где 2 это количество единиц у числа 12), к 6 (16=4х4), к 0 (20=5х4), а затем единицы повторяются, и нитка снова приходит к тем же детям: 24=6х4, 28=7х4, 32=8х4, 36=9х4, 40=10х4, 44=11х4 и наконец, 48=12х4. Мы создали пятиконечную звезду, которая будет воспроизводиться все снова и снова, как бы долго мы не двигались вперед, и даже если мы дойдем до 100=25х4 (ну, это было бы слишком амбициозно), то мы все равно получим пять пятиконечных звезд, располагающихся одна поверх другой!

o Почему таблицы на 6 и 4 дают одну и ту же геометрическую фигуру? Потому что у них есть одинаковые качества! Последняя цифра в числах таблицы умножения на 4 повторяется через каждые пять шагов (4, 8, 2, 6, 0), а у таблицы на 6 происходит то же самое, но наоборот (6, 2, 8, 4, 0). Аналогично, таблицы на 1, на 9 и на 11 порождают одинаковую десятистороннюю звезду (декагон); таблицы на 2, 8 и 12 дают пентагон; таблицы на 3 и 7 дают прекрасную десятиконечную звезду.

o Несомненно, все это может стать для второклассников замечательным открытием! Они могут обнаружить, что для любых двух чисел в сумме дающих десять, их таблицы умножения произведут одну и ту же геометрическую фигуру, но движение будет совершаться в противоположные стороны. Это происходит потому, что последние знаки в этих таблицах одинаковы, но выстроены в обратном порядке.

· Идеи для упражнений с движением можно найти в книге Хеннинга Андерсена «Активная арифметика».