Независимые испытания. Формула Бернулли

Что такое независимые испытания? Практически всё понятно уже из самого названия. Пусть производится несколько испытаний. Если вероятность появления некоего события 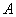в каждом из них не зависит от исходов остальных испытаний. При этом под словосочетанием «независимые испытания» часто подразумевают повторные независимые испытания– когда они осуществляются друг за другом.

Простейшие примеры:
– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.

Совершенно ясно, что вероятность выпадения орла либо решки в любом испытании не зависит от результатов других бросков. Аналогичное утверждение, естественно, справедливо и для кубика.

А вот последовательное извлечение карт из колоды не является серией независимых испытаний – как вы помните, это цепочка зависимых событий. Однако если карту каждый раз возвращать обратно, то ситуация станет «такой, какой надо».

Задача 1

Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна 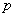. Найти вероятность того, что:

а) стрелок попадёт только один раз;
б) стрелок попадёт 2 раза.

Решение: условие сформулировано в общем виде и вероятность попадания в мишень при каждом выстреле считается известной. Она равна 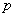(если совсем тяжко, присвойте параметру какое-нибудь конкретное значение, например, ).

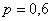Коль скоро, мы знаем 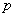, то легко найти вероятность промаха в каждом выстреле:
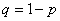, то есть, «ку» – это тоже известная нам величина.

а) Рассмотрим событие «Стрелок попадёт только один раз» и обозначим его вероятность через 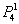(индексы понимаются как «одно попадание из 4-х»). Данное событие состоит в 4-х несовместных исходах: стрелок попадёт в 1-й или во 2-ой или в 3-й или в 4-й попытке.

По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий: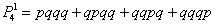

Упростим результат с помощью комбинаторной формулы количества сочетаний:
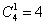способами можно выбрать попытку, в которой стрелок попал.

И, поскольку в каждом случае имеет место 1 попадание и 3 промаха, то:
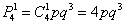– вероятность того, что стрелок попадёт только один раз из 4-х

б) Рассмотрим событие «Стрелок попадёт два раза» и обозначим его вероятность через 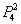(«два попадания из 4-х»). Здесь вариантов становится больше, попадания возможны:

в 1-й и 2-й попытках или в 1-й и 3-й попытках или в 1-й и 4-й попытках иливо 2-й и 3-й попытках
или во 2-й и 4-й попытках илив 3-й и 4-й попытках.

Таким образом, по тем же теоремам сложения и умножения вероятностей:

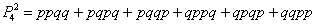
Рациональнее придерживаться более компактной схемы:
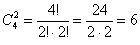способами (перечислены выше) можно выбрать 2 попытки, в которых произойдут попадания.

И, поскольку в любом исходе ровно 2 попадания и 2 промаха, то:
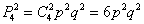– вероятность того, что стрелок попадёт 2 раза из 4-х.

Формулой Бернулли

Pn(k)=Ckn⋅pk⋅qn−k,q=1−p.

В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности
, .
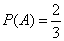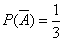По формуле Бернулли требуемая вероятность равна
.
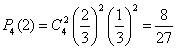