Определение множества Эджворта - Парето

Методические указания

по выполнению курсовой работы по дисциплине

«Теория принятия решений»

для студентов заочной формы обучения

Задача 1. Обоснование решений в условиях риска

Суть статистического способа заключается в том, что изучается статистика потерь и прибылей, имевших место на данном или аналогичном производстве. Устанавливаются величина и частотность получения той, или иной экономической отдачи. На основе оставляется наиболее вероятный прогноз на будущее. Применительно к экономическим задачам методы теории вероятности сводятся к определению вероятности наступления событий и к выбору из возможных событий самого предпочтительного. Исходить следует из наибольшей величины математического ожидания, которое равно абсолютной величине этого события, умноженной на вероятность его наступления.

Главные инструменты статистического метода расчета экономического риска:

- вариация

- дисперсия

- стандартное (среднеквадратическое) отклонение.

Величина риска, или степень риска, может быть измерена двумя критериями: 1) среднее ожидаемое значение, 2) колеблемость (изменчивость) возможного результата.

Среднее ожидаемое значение – это то значение величины события, которое связано с неопределенной ситуацией. Оно является средневзвешенной всех возможных результатов, где вероятность каждого результата используется в качестве частоты, или веса, соответствующего значения. Таким образом, вычисляется предположительный результат.

В ситуации риска реализуется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им соответствующих вероятностей. При этом пользуются:

ü известными, типовыми ситуациями;

ü предыдущими распределениями вероятностей на основании статистики предшествующих периодов или результатов выборочных обследований;

ü субъективными оценками, сделанными аналитиками, ЛПР самостоятельно или с привлечением экспертов.

Однако использование в качестве измерителей риска абсолютных показателей вариации не всегда является обоснованным. В частности необходимо сделать выбор наиболее рационального варианта из множества потенциально возможных решений. Возможность проведения сравнительной оценки вариантов решения дает относительный показатель вариации – коэффициент вариации ( ), который рассматривается в качестве показателя оценки степени риска. Чем больше значение коэффициента вариации, тем больше неопределенности для получения запланированного результата, и, следовательно, тем больше степень риска. Таким образом, рассматривая коэффициент вариации в качестве критерия обоснования решений в условиях риска, следует помнить, что этот критерий должен стремиться к минимуму:

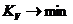
Коэффициент вариации рассчитывается как отношение среднеквадратического отклонения (σ) к математическому ожиданию случайной величины (МО), выраженное в процентах:

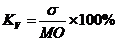
Для интерпретации полученного значения коэффициента вариации может быть использована следующая шкала:

- малая степень риска;

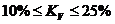- средняя степень риска;

- высокая степень риска.

Математическое ожидание случайной величины (например, ожидаемый размер прибыли) и среднеквадратическое отклонение могут быть рассчитаны следующим образом:

1. Если имеется полная информация о распределении случайной величины, используют формулы:

, ,

где x_i – прогнозная оценка случайной величины в i-м состоянии;

p_i – вероятность i-й прогнозной оценки;

.

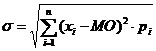2. Если известны только размах вариации случайной величины (x_min и x_max) и соответствующие вероятности (p_min и p_max) – расчет производится на основе предположения о β-распределении случайной величины с использованием формул (p_min > p_max):

;

.

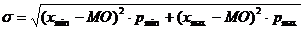3. Если известен только размах вариации (а вероятности не известны), то на основании предположения о β-распределении случайной величины величину отклонения можно оценить приближенно:

.

Задача 2. Обоснование решений в условиях неопределенности

Выбор рациональной альтернативы (стратегии) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности.

Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи представлено в виде матрицы выигрышей (a_ji) игры с природой:

Матрица игры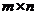

Si xj	S1	S2	…	Sn
x1	a11	a12		a1n
x2	a21	a22		a2n
…	…
xm	am1	am2		amn

x_j – стратегии сознательного игрока, ;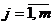

S_i – состояния природы, ;

a_ji – выигрыш сознательного игрока при использовании им стратегии x_j, если состоянием природы будет S_i.

1. Критерий Лапласа.

Данный критерий предполагает равновероятность состояний внешней среды и рекомендует выбор стратегии с максимальным средним выигрышем:

К_Л = .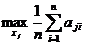

Вероятности состояний природы p_i равны между собой:

.

2. Критерий Байеса.

Этот критерий учитывает вероятности состояний природы и рекомендует выбор стратегии с максимальным среднеожидаемым выигрышем:

К_Б = , .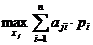

3. Критерий Вальда (максиминный критерий, критерий крайнего пессимизма, критерий наибольшей осторожности).

Данный критерий ориентируется на худшее состояние внешний среды и рекомендует выбор стратегии с максимальным гарантированным выигрышем в таких условиях:

К_В = .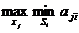

4. Критерий Сэвиджа (минимаксного риска).

Критерий минимаксного риска ориентируется на самую неблагоприятную обстановку и рекомендует выбор стратегии с минимальным риском:

К_С = .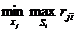

Для использования данного критерия необходимо перейти от матрицы выигрышей к матрице рисков.

Риск (r_ji) – разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием природы будет состояние S_i, и выигрышем, который игрок получит, не имея этой информации при использовании стратегии x_j:

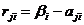, (при заданном i).

5. Критерий Гурвица (компромиссный критерий, критерий пессимизма-оптимизма).

Этот критерий учитывает индивидуальные предпочтения сознательного игрока к пессимизму и оптимизму. Для его использования необходимо задать значение коэффициента пессимизма α, α [0,1]:

К_Г = .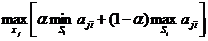

Возможны следующие характерные случаи использования критерия Гурвица:

1) если a = 1, то

К_Г¹ = .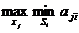

В этом частном случае критерий Гурвица совпадает с критерием Вальда (крайнего пессимизма).

2) если a = 0, то

К_Г⁰ = .

В этом частном случае критерий Гурвица совпадает с критерием крайнего оптимизма.

3) если a = 0,5, то

К_Г^0,5 = .

Задачи 3и 4. Обоснование решений в условиях многовариантности и

Многокритериальности

Для выполнения задач 3 и 4 расчетной части курсовой работы студентам необходимо применить один из методов экспертного или системного анализа для обоснования управленческих решений. Описания некоторых процедур обоснования решений приведены ниже.

Метод парных сравнений

Экспертам предлагается произвести сравнение n альтернатив А₁, А₂, …, А_n попарно, с тем, чтобы установить наиболее значимую в каждой паре. Для облегчения этой процедуры составляют матрицы парных сравнений, в которых все сопоставляемые альтернативы записываются дважды: по горизонтали и по вертикали. Каждый эксперт, заполняющий такую матрицу, должен проставить на пересечении сравниваемых альтернатив оценку с использованием определенной шкалы, например:

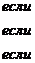
и .

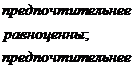
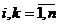Матрица парных сравнений

	А1	А2	…	Аn
А1	×	a12	…	a1n
А2	a21	×	…	a2n
…	…	…	…	…
Аn	an1	an2	…	×

Если процедура сравнения выполняется несколькими экспертами, то в результате сложения одноименных элементов частных матриц составляется суммарная матрица, отражающая предпочтения всех экспертов.

В таких условиях веса альтернатив определяются следующим образом:

· определяется цена каждой альтернативы как сумма оценок по строке матрицы –

;

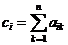· вычисляются искомые веса альтернатив путем нормирования цен альтернатив –

, .

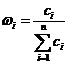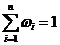Алгоритм Кемени – Снелла

Эвристический алгоритм Кемени – Снелла предназначен для определения результирующего ранжирования альтернатив. Реализуется алгоритм в несколько этапов.

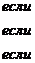
1. Исходя из частных ранжирований n альтернатив А₁, А₂, …, А_n определяются матрицы бинарных предпочтений (по каждому эксперту Э₁, Э₂, …, Э_m) с оценками :

и ..

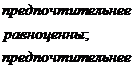
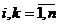Например, известны частные ранжирования 8 экспертами 4 альтернатив (в экспертизе использован метод предпочтений):

Эj	Аi
А1	А2	А3	А4
Э1
Э2
Э3
Э4
Э5
Э6
Э7
Э8

Исходя из указанных частных ранжирований, определяем матрицы бинарных предпочтений каждого эксперта с оценками .

Э1

А1

А2

А3

А4

Э2

А1

А2

А3

А4

Э3

А1

А2

А3

А4

Э4

А1

А2

А3

А4

А1

×

-1

-1

+1

А1

×

+1

+1

+1

А1

×

-1

-1

+1

А1

×

+1

-1

+1

А2

+1

×

-1

+1

А2

-1

×

+1

+1

А2

+1

×

+1

+1

А2

-1

×

-1

-1

А3

+1

+1

×

+1

А3

-1

-1

×

+1

А3

+1

-1

×

+1

А3

+1

+1

×

+1

А4

-1

-1

-1

×

А4

-1

-1

-1

×

А4

-1

-1

-1

×

А4

-1

+1

-1

×

Э5

А1

А2

А3

А4

Э6

А1

А2

А3

А4

Э7

А1

А2

А3

А4

Э8

А1

А2

А3

А4

А1

×

-1

-1

+1

А1

×

+1

-1

-1

А1

×

-1

+1

А1

×

-1

+1

А2

+1

×

+1

А2

-1

×

-1

-1

А2

+1

×

+1

+1

А2

×

-1

+1

А3

+1

×

+1

А3

+1

+1

×

+1

А3

-1

×

+1

А3

+1

+1

×

+1

А4

-1

-1

-1

×

А4

+1

+1

-1

×

А4

-1

-1

-1

×

А4

-1

-1

-1

×

2. Определяется матрица потерь с оценками :

, .

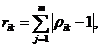
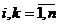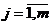По данным примера определим матрицу потерь с оценками :

Матрица потерь

	А1	А2	А3	А4
А1	×	9
А2		×
А3			×
А4				×

Например, элемент 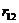рассчитан следующим образом:

.

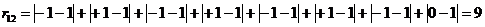3. Выполняется обработка матрицы потерь в несколько циклов. В каждом цикле рассчитываются суммы оценок потерь по строкам матрицы, находится альтернатива с минимальной суммой, которая исключается из матрицы потерь.

Выполним обработку матрицы потерь по данным примера:

Циклы вычислений
А1	24 (=9+13+2)	11 (=9+2) ←min А1 исключается из матрицы	-
А2	20 (=7+9+4)	11 (=7+4) ←min А2 исключается из матрицы	-
А3	10 (=3+7+0)←min А3 исключается из матрицы	-	-
А4	42 (=14+12+16)	26 (=14+12)

4. Находится результирующее ранжирование альтернатив (ранжирование определяется порядком исключения альтернатив из матрицы потерь).

Результирующее ранжирование альтернатив в примере получено таким: .

Метод анализа иерархий

Метод анализа иерархий (МАИ) разработан американским исследователем Томасом Саати. Этот метод ориентирован на сложные системные задачи с плохой структурой (слабоструктуризованные и неструктуризованные), которые решаются в условиях многовариантности, многокритериальности, неопределенности и риска.

Метод основан на структуризации решаемой задачи в виде многоуровневой иерархической модели (выполняется декомпозиция решаемой сложной задачи на более простые составляющие) и активном использовании процедур парных сравнений, учитывающих субъективные предпочтения ЛПР.

МАИ прошел апробацию и доказал свою эффективность на самых разных уровнях управления; позволяет работать с неполными и неточными исходными данными, представленными в различной форме – в виде количественных оценок, качественных оценок, оценок типа «да» - «нет», интервальных оценок, результатов ранжирования и др.; постоянно развивается и используется в компьютерных системах поддержки принятия решений различных уровней и назначения (например, Expert Choice, Decide, ПРАИС).

Недостатком метода является большой объем данных, которые запрашиваются у пользователя СППР в процессе решения сложной системной задачи.

На основе МАИ могут быть решены следующие задачи:

ü задачи планирования и управления (планирование инвестиций, разработка программ развития предприятий, отраслей экономики, территорий и др.);

ü задачи проектирования (выбор проектов строительства сооружений различного назначения, вариантов конструкций, модификаций изделий и др.);

ü задачи прогнозирования (разработка сценариев развития отраслей экономики, научных направлений и различных систем);

ü задачи реинжиниринга бизнес-процессов и организаций;

ü задачи принятия компромиссных решений в конфликтных ситуациях.

Для реализации процедур парных сравнений (при заполнении матриц парных сравнений) Т. Саати предложил использование следующей шкалы оценок:

1 – А_j и А_i одинаково важны;

3– А_j незначительно важнее, чем А_i;

5– А_j значительно важнее, чем А_i;

7 – А_j явно важнее, чем А_i;

9– А_j абсолютно превосходит А_i.

Примечание: j - строки, i - столбцы матрицы; допускаются промежуточные оценки 2, 4, 6, 8 и используются обратные (например, ⅓, ⅛).

Матрице парных сравнений свойственна обратная симметричность: интенсивность предпочтения А_j над А_i обратна интенсивности предпочтения А_i над А_j.

Для расчета весов критериев и получения оценок альтернатив по результатам парных сравнений Т. Саати разработал 4 вычислительных приближенных алгоритма (методы получения приоритетов объектов сравнения):

1. Суммируются элементы каждой строки матрицы; полученные значения нормируются - сумма каждой строки делится на общую сумму.

2. Элементы столбцов суммируются; для каждой суммы находится обратное значение; полученные значения нормируются.

3. Каждый элемент столбца нормируется относительно суммы элементов по столбцу; нормированные элементы строк суммируются; полученные значения делятся на n - число альтернатив или критериев (объектов).

4. Для каждой строки находится средняя геометрическая величина (n элементов строки перемножаются, и извлекается корень степени n); полученные значения нормируются.

Указанные алгоритмы обеспечивают достаточную для практики точность, причем они расположены в порядке возрастания точности – наилучшее приближение дает применение четвертого алгоритма. Точное решение получается путем возведения матрицы в произвольно большие степени и деления суммы каждой строки на общую сумму элементов матрицы.

Оценка степени согласованности при заполнении матрицы парных сравнений производится по формуле:

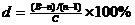
где В – расчетная величина, получаемая следующим образом: суммируются оценки по каждому столбцу матрицы, затем сумма каждого столбца умножается на вес соответствующей альтернативы, после этого полученные значения суммируются;

С – коэффициент, определяемый по данным таблицы:

n
С			0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49

Если d≤20%, то достигнута приемлемая степень согласованности при заполнении матрицы парных сравнений. В противном случае необходимо пересмотреть исходные данные и заново заполнить матрицу парных сравнений.

Рассмотрим сущность метода на примере выбора рационального варианта для размещения офиса.

Некоторая фирма провела анализ рынка офисных помещений и отобрала несколько потенциально возможных вариантов:

Критерии оценки альтернатив	Варианты офисных помещений
А1	А2	А3	А4	А5
К1 – общая площадь помещений, кв.м
К2 – состояние помещений	требуется ремонт	не требуется ремонт	требуется ремонт	требуется ремонт	выполнен косметический ремонт
К3 – возможность парковки	нет	нет	есть	нет	есть
К4 – уровень телефонизации, кол-во линий
К5 – стоимость помещений, у.е./кв.м

Система предпочтений на множестве частных критериев: К₁, К₂, К₅, К₃, К₄.

Множество Парето оптимальных вариантов офисных помещений – А₂, А₃, А₅.

Определим рациональный вариант для размещения офиса на основе МАИ.

Этап 1.Решаемая задача представляется в виде многоуровневой иерархической модели

Рациональный офис

Уровень1

(стратегическая цель)

К5

К4

К3

К2

К1

Уровень 2

(множество критериев)

А5

А3

А2

Уровень 3

(множество альтернатив)

Этап 2.Выполняется сравнение критериев попарно по их важности; рассчитываются веса частных критериев

Используя шкалу оценок Т. Саати, заполняем матрицу парных сравнений критериев по важности:

	К1	К2	К3	К4	К5
К1
К2	1/2
К3	1/6	1/5			1/3
К4	1/8	1/7	1/3		1/5
К5	1/4	1/2

Расчет весов частных критериев произведем по алгоритму 4:

Находим средние геометрические по строкам матрицы (извлекаем корень 5-й степени из произведений элементов строк матрицы):

К₁ – 3,288; К₂ – 2,036; К₃ – 0,506; К₄ – 0,260; К₅ – 1,134.

Нормализуем полученные значения (делим каждую среднюю на общую сумму):

3,288+2,036+0,506+0,260+1,134=7,224;

ω₁ = 3,288/7,224 = 0,455; ω₂ = 2,036/7,224 = 0,282; ω₃ = 0,07; ω₄ = 0,036; ω₅ =0,157.

Этап 3. Выполняется сравнение альтернатив попарно по их предпочтительности по каждому критерию в отдельности

Используя ту же шкалу оценок, заполняем матрицы парных сравнений альтернатив по каждому критерию и рассчитываем оценки альтернатив по алгоритму 4:

К1	А2	А3	А5	оценка альтернативы
А2		1/9	1/2	0,07
А3				0,80
А5		1/8		0,13
К2	А2	А3	А5	оценка альтернативы
А2				0,75
А3	1/8		1/5	0,06
А5	1/6			0,19
К3	А2	А3	А5	оценка альтернативы
А2		1/7	1/7	0,06
А3				0,47
А5				0,47

К4	А2	А3	А5	оценка альтернативы
А2			1/4	0,25
А3	1/6		1/8	0,06
А5				0,69
К5	А2	А3	А5	оценка альтернативы
А2		1/8	1/3	0,08
А3				0,83
А5		1/7		0,09

Этап 4.Определяются обобщенные скалярные оценки альтернатив

Находится сумма произведений оценок, полученных каждой альтернативой в парных сравнениях по каждому критерию, и весов соответствующих критериев:

Q(A₂)= 0,07·0,455+0,75·0,282+0,06·0,07+0,25·0,036+0,08·0,157=0,27;

Q(A₃)=0,546; (max)

Q(A₅)=0,185.

Этап 5. Выбирается рациональное решение по критерию максимума обобщенной скалярной оценки

Наибольшее значение обобщенной скалярной оценки получено у варианта А₃, следовательно, он и является рациональным вариантом для размещения офиса фирмы.

Метод функционально стоимостного анализа (ФСА)

Метод ФСА предусматривает двухкритериальную оценку альтернатив – по критерию эффективности (Э) и критерию стоимости (С). Метод ФСА включает 5 основных операций:

1) построение модели эффективности;

2) построение модели стоимости;

3) формирование альтернатив (вариантов решений);

4) построение обобщающего критерия;

5) выбор рациональной альтернативы.

При построении моделей используется вся объективная и субъективная информация. Выходные данные моделей синтезируются в обобщающий критерий, позволяющий анализировать альтернативные варианты. Базируясь на обобщенных оценках альтернатив, возможно выбрать рациональное решение. Выбор обобщающего критерия осуществляется на основе субъективных суждений лица, принимающего решение (ЛПР).

Обобщающий критерий может иметь следующий вид:

ü максимум эффективности при фиксированной стоимости: ;

ü минимум стоимости при постоянной эффективности:

;

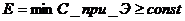ü максимум удельной эффективности:

;

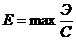ü минимум удельной стоимости:

;

ü максимум разности эффективности и стоимости:

.

Методические указания

по выполнению курсовой работы по дисциплине

«Теория принятия решений»

для студентов заочной формы обучения

Задача 1. Обоснование решений в условиях риска

Суть статистического способа заключается в том, что изучается статистика потерь и прибылей, имевших место на данном или аналогичном производстве. Устанавливаются величина и частотность получения той, или иной экономической отдачи. На основе оставляется наиболее вероятный прогноз на будущее. Применительно к экономическим задачам методы теории вероятности сводятся к определению вероятности наступления событий и к выбору из возможных событий самого предпочтительного. Исходить следует из наибольшей величины математического ожидания, которое равно абсолютной величине этого события, умноженной на вероятность его наступления.

Главные инструменты статистического метода расчета экономического риска:

- вариация

- дисперсия

- стандартное (среднеквадратическое) отклонение.

Величина риска, или степень риска, может быть измерена двумя критериями: 1) среднее ожидаемое значение, 2) колеблемость (изменчивость) возможного результата.

Среднее ожидаемое значение – это то значение величины события, которое связано с неопределенной ситуацией. Оно является средневзвешенной всех возможных результатов, где вероятность каждого результата используется в качестве частоты, или веса, соответствующего значения. Таким образом, вычисляется предположительный результат.

В ситуации риска реализуется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им соответствующих вероятностей. При этом пользуются:

ü известными, типовыми ситуациями;

ü предыдущими распределениями вероятностей на основании статистики предшествующих периодов или результатов выборочных обследований;

ü субъективными оценками, сделанными аналитиками, ЛПР самостоятельно или с привлечением экспертов.

Однако использование в качестве измерителей риска абсолютных показателей вариации не всегда является обоснованным. В частности необходимо сделать выбор наиболее рационального варианта из множества потенциально возможных решений. Возможность проведения сравнительной оценки вариантов решения дает относительный показатель вариации – коэффициент вариации ( ), который рассматривается в качестве показателя оценки степени риска. Чем больше значение коэффициента вариации, тем больше неопределенности для получения запланированного результата, и, следовательно, тем больше степень риска. Таким образом, рассматривая коэффициент вариации в качестве критерия обоснования решений в условиях риска, следует помнить, что этот критерий должен стремиться к минимуму:

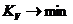
Коэффициент вариации рассчитывается как отношение среднеквадратического отклонения (σ) к математическому ожиданию случайной величины (МО), выраженное в процентах:

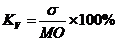
Для интерпретации полученного значения коэффициента вариации может быть использована следующая шкала:

- малая степень риска;

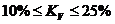- средняя степень риска;

- высокая степень риска.

Математическое ожидание случайной величины (например, ожидаемый размер прибыли) и среднеквадратическое отклонение могут быть рассчитаны следующим образом:

1. Если имеется полная информация о распределении случайной величины, используют формулы:

, ,

где x_i – прогнозная оценка случайной величины в i-м состоянии;

p_i – вероятность i-й прогнозной оценки;

.

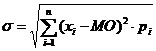2. Если известны только размах вариации случайной величины (x_min и x_max) и соответствующие вероятности (p_min и p_max) – расчет производится на основе предположения о β-распределении случайной величины с использованием формул (p_min > p_max):

;

.

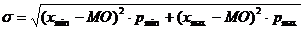3. Если известен только размах вариации (а вероятности не известны), то на основании предположения о β-распределении случайной величины величину отклонения можно оценить приближенно:

.

Задача 2. Обоснование решений в условиях неопределенности

Выбор рациональной альтернативы (стратегии) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности.

Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи предста