Контрольный тест после изучения раздела I « Интегральное исчисление и дифференциальные уравнения»
1). Вставить пропущенное слово: функция 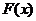 называется первообразной для функции
называется первообразной для функции 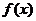 на множестве
на множестве 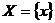 , если ……………… этой функции и дифференциал равны соответственно
, если ……………… этой функции и дифференциал равны соответственно 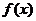 и
и  , то есть
, то есть  и
и 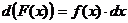 .
.
2). Что такое неопределенный интеграл функции?
1. Совокупность всех первообразных функций;
2.сумма всех значений функции;
3. произведение функции на ее производную;
4. квадрат дифференциала.
3). Как называется интеграл один из пределов который бесконечен?
1. неопределенный; 2. собственный;
3. несобственный; 4. замечательный.
4). Выберите правильный ответ:
Геометрический смысл определенного интеграла состоит в том, что определенный интеграл равен:
1. мгновенной скорости движения тела;
2. длине дуги в прямоугольных координатах;
3. объему тела вращения;
4. площади соответствующей криволинейной трапеции.
5) Среди приведенных ниже высказываний найдите ошибочные:
1. Интеграл произведения нескольких функций есть произведение интегралов от этих функций;
2. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная;
3. Определенный интеграл можно вычислить с помощью формулы Ньютона-Лейбница;
4. Величина определенного интеграла не зависит от обозначения переменной интегрирования.
6). Интеграл  вычисляется с помощью замены
вычисляется с помощью замены
1) 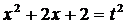 ; 2)
; 2) 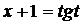 ; 3)
; 3) 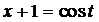 ; 4)
; 4) 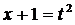 .
.
7).Найти первообразную функции 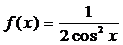 , график которой проходит через точку
, график которой проходит через точку 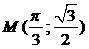
8). Вычислить площадь фигуры, ограниченной линиями у=х2–2х+1, у =2.
1). 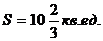 2).
2). 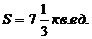 3).
3). 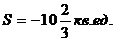 4)
4) 
9). Интеграл вида:  вычисляется по формуле интегрирования по частям, если f(x) равно:
вычисляется по формуле интегрирования по частям, если f(x) равно:
1) 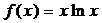 ; 2)
; 2) 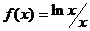 ; 3)
; 3)  ; 4)
; 4) 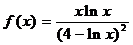 .
.
10).Найти первообразную функции f(x)=3x2–1, график которой проходит через точку M(0;2):
1). F(x) = x3 – x + 2; 2). f `(x) = x3 – x + 2;
3). F(x) = x3 – x + C; 4) f `(x) = x3 – x + C.
11). Определить тип дифференциального уравнения 
1. Линейное; 2. Бернулли; 3. Однородное; 4. С разделяющимися переменными
12). Укажите общее решение дифференциального уравнения 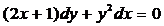
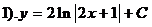 ;
; 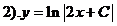 ;
; 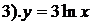 ;
;  .
.
13). Дано линейное однородное дифференциальное уравнение  Найти его общее решение.
Найти его общее решение.
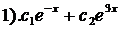 ;
; 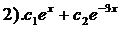 ;
; 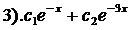 ;
; 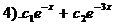 .
.
14). Дифференциальным уравнением называется любое уравнение, содержащее …………, искомую функцию и ее производные любых порядков.
1. Независимую переменную; 2. Зависимую переменную;
3. Первообразную функции; 4. Неизвестный параметр.
15). Линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида:
1. 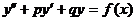 2.
2. 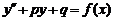 3.
3. 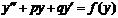 4.
4.  .
.
16). Если характеристическое уравнение линейного дифференциального уравнения второго порядка с постоянными коэффициентами имеет один корень  (два совпавших корня), то общее решение данного уравнения имеет вид:
(два совпавших корня), то общее решение данного уравнения имеет вид:
1).  2)
2)  3)
3) 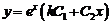 4).
4). 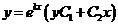 .
.
17). Укажите тип дифференциального уравнения: 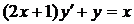
1. С разделяющимися переменными; 2. Однородное; 3. Линейное.
18). Дано линейное однородное дифференциальное уравнение  . Найти его общее решение.
. Найти его общее решение.
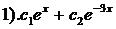
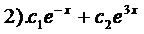
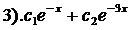

РАЗДЕЛ II. РЯДЫ
Глава 4. ЧИСЛОВЫЕ РЯДЫ
Основные понятия. Сходимость ряда. Необходимый признак сходимости
Определение.Числовым рядом называется бесконечная последовательность чисел 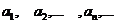 , соединенных знаком сложения, то есть
, соединенных знаком сложения, то есть
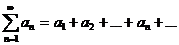 (13.1)
(13.1)
где числа 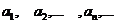 называются членами ряда,
называются членами ряда, 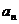 - общим членом ряда.
- общим членом ряда.
Ряд (13.1) считается заданным, если известен его общий член 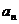 .
.
Пример.
1) 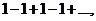
2) 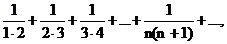
3) 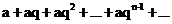
Ряд можно задать с помощью общего члена, например, 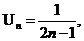 определяет следующий ряд:
определяет следующий ряд: 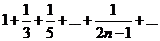
Определение. Частичной суммой 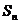 числового ряда называетсясуммаего первых n членов,
числового ряда называетсясуммаего первых n членов,
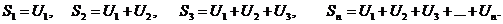
Определение.Суммой числового ряда S называется предел последовательности его частичных сумм, если этот предел существует
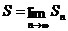 ,
,
причем ряд называется сходящимся, в противном случае, если же 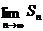 не существует, или
не существует, или 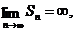 то ряд называется расходящимся.
то ряд называется расходящимся.
Пример.Исследовать на сходимость ряды
а). 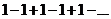
б). 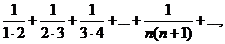
Решение:
а). Рассмотрим ряд 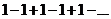 . Найдем его частичные суммы
. Найдем его частичные суммы 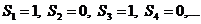 Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
Последовательность его частичных сумм 1,0,1,0.1,0... не имеет предела, следовательно ряд расходится.
б). Рассмотрим ряд
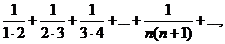
найдем его частичные суммы:
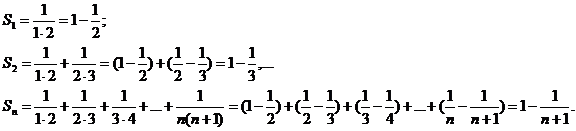
Так как 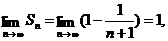 то рассматриваемый ряд сходится: его сумма равна 1.
то рассматриваемый ряд сходится: его сумма равна 1.
