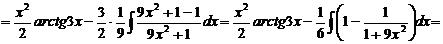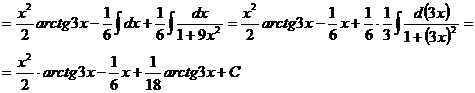Глава 1. неопределенный интеграл
Первообразная функция и неопределенный интеграл
Определение. Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x)
Определение. Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 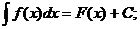
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства неопределенного интеграла
1. 
2. 
3. 
4. 
где u, v, w – некоторые функции от х.
5. 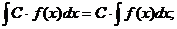
Таблица основных интегралов
| Интеграл | Значение | Интеграл | Значение | ||
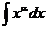 | 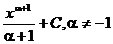 | 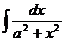 | 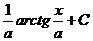 | ||
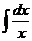 | 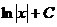 | 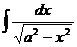 | arcsin  + C + C | ||
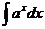 | 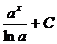 | 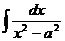 | 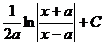 | ||
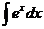 | ex + C | 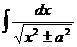 | ln 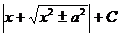 | ||
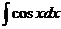 | sinx + C | 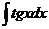 | -ln½cosx½+С | ||
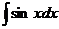 | -cosx + C | 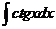 | ln½sinx½+ C | ||
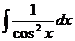 | tgx + C | 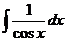 | 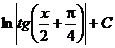 | ||
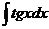 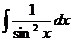 | -ctgx + C | 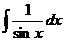 | 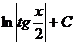 |
Методы интегрирования
1. Непосредственное интегрирование.Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием.
Пример.
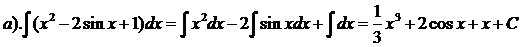
Проверка:
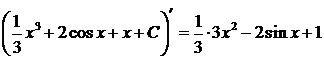
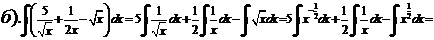
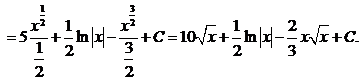
Проверка:
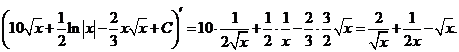
2. Способ подстановки (замены переменных).Если требуется найти интеграл 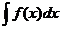 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
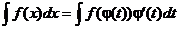
Пример.
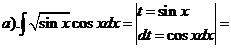
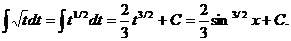
Проверка:
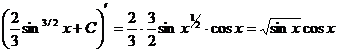
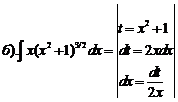
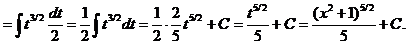
Проверка:
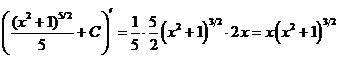
Интегрирование по частям
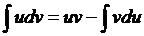
Формула интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Замечание: Если в подынтегральной функции имеется множитель вида 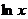 ,
, 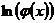 ,
, 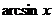 ,
, 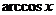 ,
, 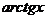 ,
, 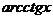 , то их удобно принимать в качестве
, то их удобно принимать в качестве 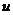 , так как они легче дифференцируются.
, так как они легче дифференцируются.
Если подынтегральная функция имеет вид 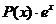 ,
, 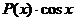 ,
, 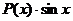 ,
, 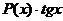 ,
, 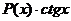 , то за
, то за 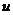 удобно принимать
удобно принимать 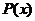 , где
, где 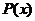 - это некоторый многочлен, причем формулу интегрирования по частям необходимо применять столько раз, какова степень многочлена.
- это некоторый многочлен, причем формулу интегрирования по частям необходимо применять столько раз, какова степень многочлена.
Пример.
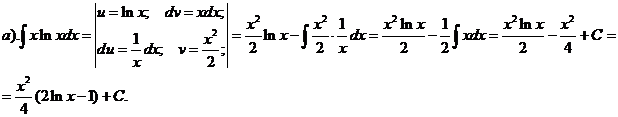 Проверка:
Проверка:
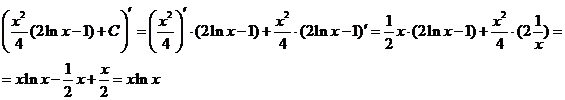
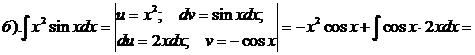
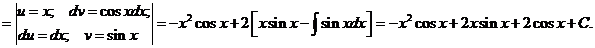 Проверка:
Проверка:
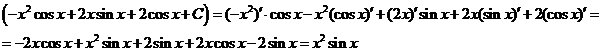
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Примеры решения типовых задач
№ 1. Найти интеграл следующих функций:
а). 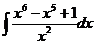 б).
б). 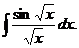 в).
в). 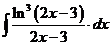 г).
г). 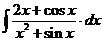
д). 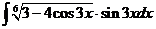 е).
е). 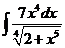 ж).
ж). 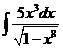 з).
з). 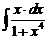
и). 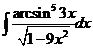 к).
к). 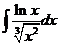 л).
л). 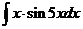 м).
м). 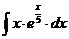 н).
н). 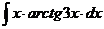
Решение:
а). 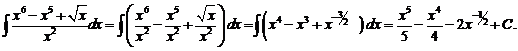
б) Воспользуемся подстановкой x=t2. Тогда 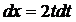 , получим:
, получим:
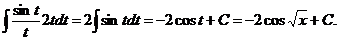
в). Если под интегралом содержится логарифмическая функция, то удобно принять ее за новую переменную, если под знаком интеграла присутствует производная этой функции (с точностью до постоянного множителя).
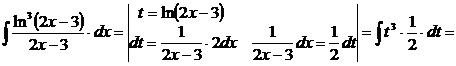
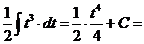
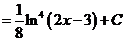
г). 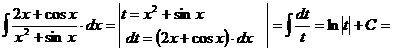

д). За новую переменную удобно взять подкоренное выражение, если под интегралом присутствует также его производная с точностью до постоянного множителя.
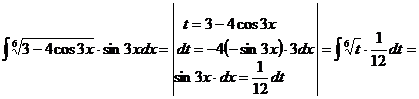
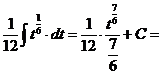
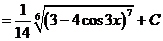
е). 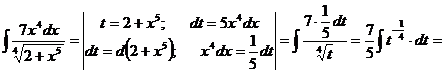
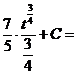
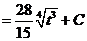
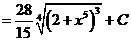
ж). Новая переменная иногда выбирается из следующих соображений: в знаменателе стоит разность постоянной и квадрата некоторой функции. Эту функцию мы принимаем за новую переменную, если в числителе присутствует ее производная (с точностью до постоянного множителя).
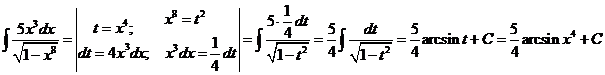 з). Подстановка выбирается аналогично предыдущему примеру.
з). Подстановка выбирается аналогично предыдущему примеру.
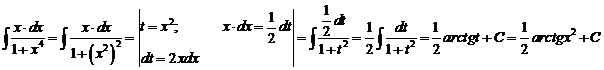
и). За новую переменную иногда выбирают функцию, стоящую в основании степени, если подынтегральное выражение содержит производную этой функции с точностью до постоянного множителя. 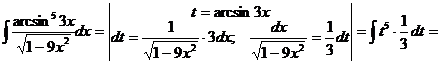
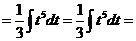
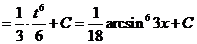
к). 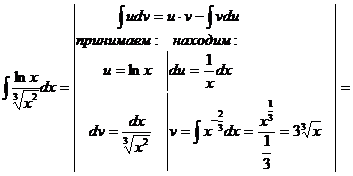
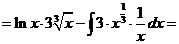
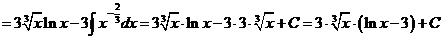
л). 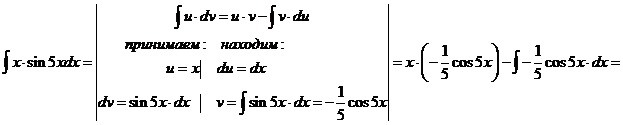
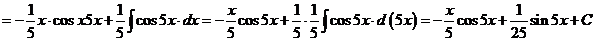
м). 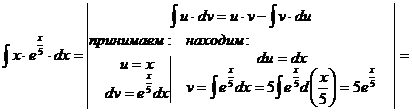
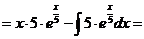
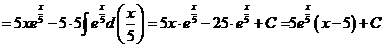
н). 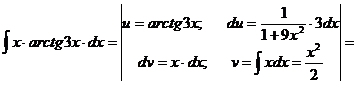
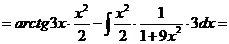
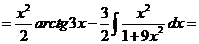
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем вчислителе прибавим иотнимем единицу, после чего разобьем интеграл на два табличных: