Тема 5. ФункциИ двух независимых переменных
При изучении этой темы следует усвоить определения частных производных и правила их вычисления, обратить внимание на схему нахождения частных производных высших порядков. При решении задач на экстремум нужно придерживаться последовательности действий по исследованию функции.
Вопросы для изучения и самопроверки
1. Определение функции двух и нескольких переменных. Область определения.
2. Частные производные функции двух переменных.
3. Полный дифференциал функции двух переменных.
4. Частные производные высших порядков.
5. Условия экстремума функции двух переменных.
6. Схема исследования функции двух переменных на экстремум.
Задачи 121 –140.Найти частные производные 1–го порядка функции двух переменных.
121. а) 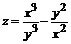 ; ; | б) 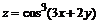 . . |
122. а) 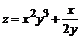 ; ; | б) 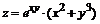 . . |
123. а) 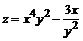 ; ; | б) 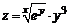 . . |
124. а) 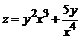 ; ; | б) 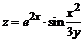 . . |
125. а) 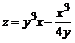 ; ; | б) 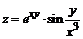 . . |
126. а) 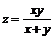 ; ; | б) 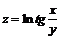 . . |
127. а) 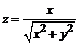 ; ; | б) 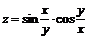 . . |
128. а) 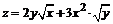 ; ; | б) 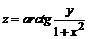 . . |
129. а) 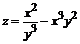 ; ; | б) 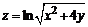 . . |
130. а) 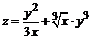 ; ; | б) 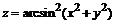 . . |
131. а) 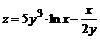 ; ; | б) 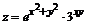 . . |
132. а) 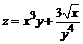 ; ; | б) 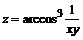 . . |
133. а) 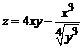 ; ; | б) 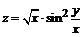 . . |
134. а) 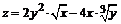 ; ; | б) 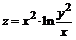 . . |
135. а) 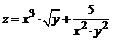 ; ; | б) 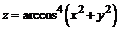 . .  |
136. а) 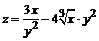 ; ; | б) 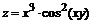 . . |
137. а) 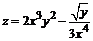 ; ; | б) 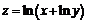 . . |
138. а) 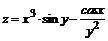 ; ; | б) 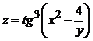 . . |
139. а) 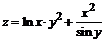 ; ; | б) 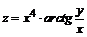 . . |
140. а) 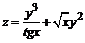 ; ; | б) 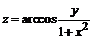 . . |
Решение типовых примеров
П р и м е р ы. Найти частные производные 1-го порядка заданных функций..
1. 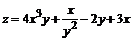 .
.
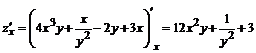 .
.
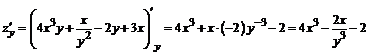 .
.
2. 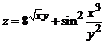 .
.
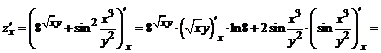
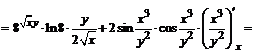
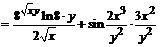 ;
;
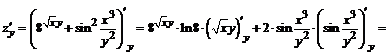
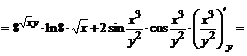
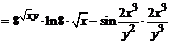 .
.
Задачи 141–160.Исследовать на экстремум заданные функции.
141. 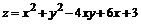 .
.
142. 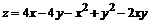 .
.
143. 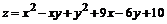 .
.
144. 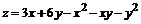 .
.
145. 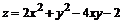 .
.
146. 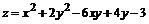 .
.
147. 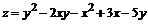 .
.
148. 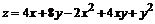 .
.
149. 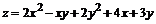 .
.
150. 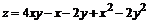 .
.
151. 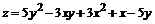 .
.
152. 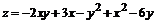 .
.
153. 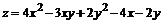 .
.
154. 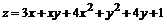 .
.
155. 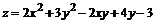 .
.
156. 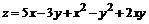 .
.
157. 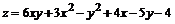 .
.
158. 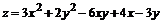 .
.
159. 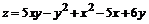 .
.
160. 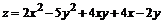 .
.
Решение типового примера
Найти экстремум функции 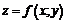 , если
, если 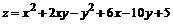 .
.
Р е ш е н и е.
1. Областью определения функции являются все точки координатной плоскости 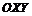 .
.
2. Находим частные производные первого порядка:
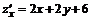 ;
; 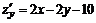 .
.
Приравняем частные производные к нулю, решив полученную систему, получим критическую точку
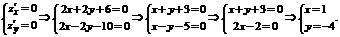
Точка 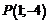 – стационарная, подозрительная на экстремум.
– стационарная, подозрительная на экстремум.
3. Находим частные производные второго порядка:
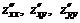 ;
;
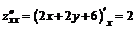 ;
; 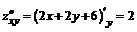 ;
; 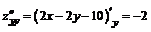 .
.
Таким образом получаем
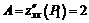 ;
; 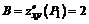 ;
; 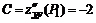 .
.
Составим выражение 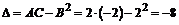 .
.
Так как 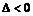 следовательно точка
следовательно точка 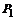 не является точкой экстремума.
не является точкой экстремума.
Тема 6. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Для решения задач по этой теме нужно обратить внимание на определения первообразной и неопределенного интеграла, свойства неопределенного интеграла, усвоить таблицу основных интегралов и основные методы интегрирования. Успех в решении задач достигается правильным выбором метода интегрирования и накопленным опытом вычисления интегралов. Особое внимание уделить методам подстановки и интегрирования по частям. При вычислении интегралов от рациональных дробей нужно усвоить методику разложения рациональных дробей на простейшие дроби и их интегрирование.
Вопросы для изучения и самопроверки
1. Понятие первообразной.
2. Неопределенный интеграл и его свойства.
3. Таблица интегралов.
4. Основные методы интегрирования.
5. Рациональные дроби, разложение на простейшие дроби.
6. Интегрирование простейших дробей.
7. Интегрирование рациональных дробей.
Задачи 161–180.Найти неопределенные интегралы и результаты проверить дифференцированием.
161. а) 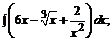 б)
б) 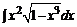 ;
;
в) 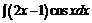 .
.
162. а) 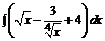 ; б)
; б) 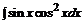 ;
;
в)  .
.
163. а) 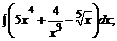 б)
б) 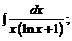
в) 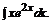
164.а) 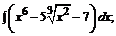 б)
б) 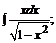
в) 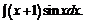
165. а) 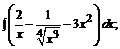 б)
б) 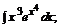
в) 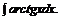
166. а) 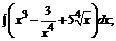 б)
б) 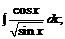
в) 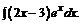
167. а) 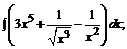 б)
б) 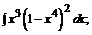
в) 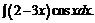
168. а) 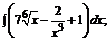 б)
б) 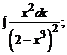
в) 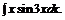
169. а) 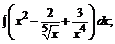 б)
б) 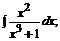
в) 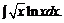
170. а) 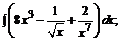 б)
б) 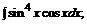
в) 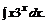
171. а) 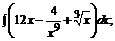 б)
б) 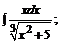
в) 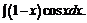
172. а) 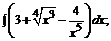 б)
б) 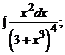
в) 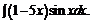
173. а) 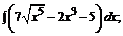 б)
б) 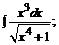
в) 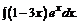
174. а) 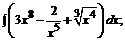 б)
б) 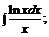
в) 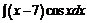
175. а) 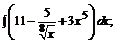 б)
б) 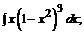
в) 
176. а) 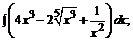 б)
б) 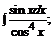
в)  .
.
177. а) 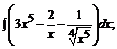 б)
б) 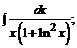
в) 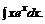
178. а) 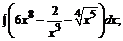 б)
б) 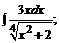
в) 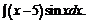
179. а) 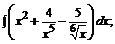 б)
б) 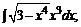
в) 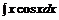
180. а) 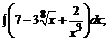 б)
б) 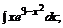

в) 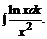
Решение типовых примеров
При решении примеров рекомендуется использовать свойства неопределенного интеграла, таблицу интегралов, применять методы замены переменной и интегрирования по частям в неопределенном интеграле.
Основная таблица интегралов
1. 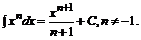 2.
2. 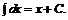
3. 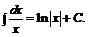 4.
4. 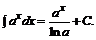
5. 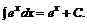 6.
6. 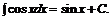
7. 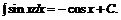 8.
8. 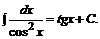
9. 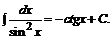 10.
10. 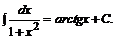
11. 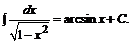
П р и м е р ы.Найти неопределенные интегралы и результаты проверить дифференцированием.
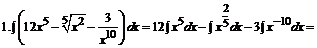
= 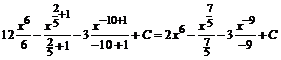 =
=
= 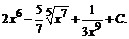
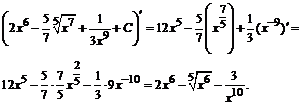
При решении примера использовались свойства степени: 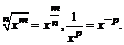
2. 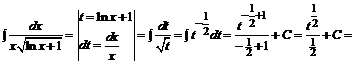
= 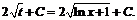
При решении примера применялся метод замены переменной.
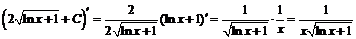 .
.
3. 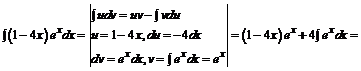
= 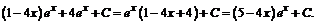
При решении примера применялся метод интегрирования по частям.