Дифференциальное уравнение упругой линии балки примет вид

.

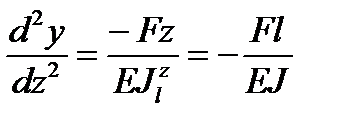Последовательно интегрируя данное уравнение, получим:

;

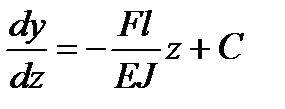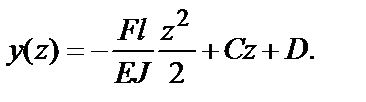
Постоянные интегрирования находим из начальных условий:

при z = l ;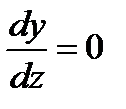

при z = l y(z) = 0.

Из первого уравнения из начальных условий

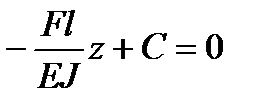, откуда ;

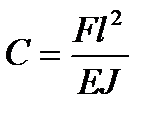Из второго уравнения из начальных условий

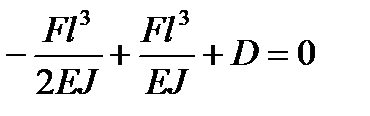, откуда .

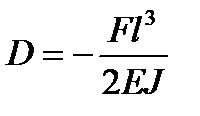Подставляя найденные значения постоянных интегрирования в уравнения перемещений балки при z = 0, получим:

;

.

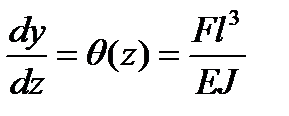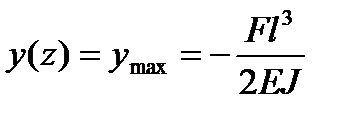В балке постоянного сечения по длине

.

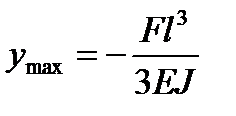Следовательно, балки равного сопротивления изгибу, обладая такой же прочностью в заделке, как и балка постоянного сечения, имеют в полтора раза больший прогиб. Подобного рода системы используются в технике при изготовлении рессор, которые должны обладать достаточной прочностью и большой гибкостью. Так, например, обыкновенная автомобильная рессора имеет такой же закон изменения жесткости, как рассмотренная выше балка.

9.12. Расчет статически неопределимых балок.

Основная система. Расчетные уравнения.

Теорема о трех моментах. Способ сравнения деформаций

Неразрезными называют балки, лежащие более чем на двух опорах и не имеющие промежуточных шарниров. Они являются статически неопределимыми и рассчитываются с помощью метода сил.

У статически определимой балки должно быть три реакции (для плоской задачи, рис. 9.29).

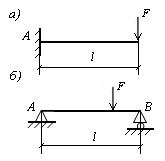
Рис. 9.29. Схемы статически

определимых балок

С добавлением промежуточных опор балка становится статически неопределимой (рис. 9.30). Степень статической неопределимости определяется по формуле

S = n – 3,

где n – число опорных связей для балки (рис. 9.30).

S = 5 – 3 = 2.

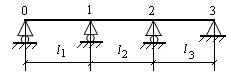
Рис. 9.30. Схема неразрезной балки

Если все опоры являются шарнирными (одна опора обязательно должна быть неподвижной), то степень статической неопределимости определяется по количеству внутренних опор. Опоры нумеруются слева направо, начиная с 0. Номер пролета определяется номером правой опоры.

Рассмотрим многопролетную балку, опирающуюся на m шарнирных опор (рис. 9.31, а). У такой балки возникает m вертикальных реакций, и она является (m – 2) раза статически неопределимой. Для решения задачи выбираем основную систему (О.С.). Для неразрезной балки наиболее рациональной основной системой является основная система с врезанными над внутренними опорами шарнирами (рис. 9.31, б).

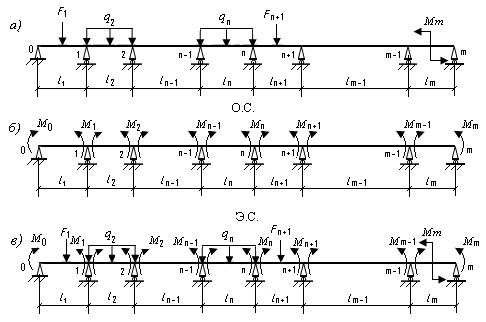
Рис. 9.31. Заданная, основная и эквивалентная системы неразрезной балки

При этом неразрезная балка распадается на отдельные однопролетные балки, имеющие по одной общей опоре. Лишними неизвестными являются изгибающие моменты в опорных сечениях. Действие заданной нагрузки распространяется только на пролет, в котором она приложена. Влияние ее на другие пролеты выражается опорными изгибающими моментами М_i.

Эквивалентной системой (Э.С.) называется ряд простых шарнирно опертых балок, нагруженных заданной нагрузкой и неизвестными изгибающими моментами x_i (рис. 9.31, в). Таким образом,

М₁ = х₁; М₂ = х₂; …; М_п = х_п,

направления моментов приняты положительными.

Составим уравнение совместности деформаций, которое выражает отсутствие взаимного угла поворота сечений над промежуточными опорами (рис. 9.32).

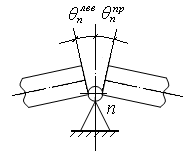
Рис. 9.32. Схема деформаций n

Промежуточного шарнира

Таким образом, ; .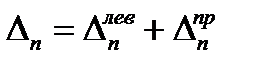

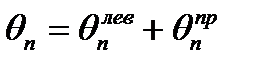Поскольку основная система состоит из отдельных двух опорных балок, то для решения уравнения совместности деформаций требуется рассмотреть только два пролета, примыкающих к n-й опоре, т. е. пролеты (n – 1) и (n + 1).

Таким образом, от полного канонического уравнения по n-му направлению

х₀δ_п0 + х₁δ_п1 + х₂δ_п2 + … + х_п-1δ_п(п-1) + х_пδ_пп + х_п+1δ_п(п+1) + …+ х_mδ_пm +

+ Δ_пр = 0,

останется уравнение

х_п–1δ_п(п–1) + х_пδ_пп + х_п+1δ_п(п+1) + Δ_пр = 0.

Все остальные коэффициенты вида δ_ij равны нулю, так как единичная эпюра 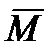от х_п распространяется только на два прилегающих пролета (рис. 9.33, а).

Учитывая, что EJ = const, применим способ Верещагина и определим коэффициенты и свободный член полученного уравнения:

;

;

;

.

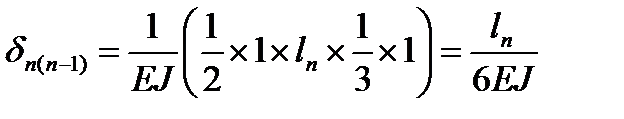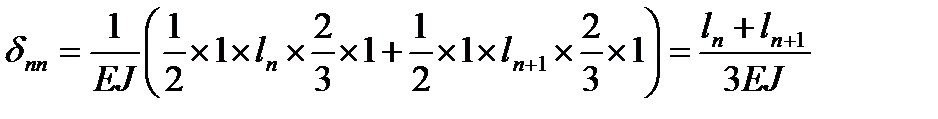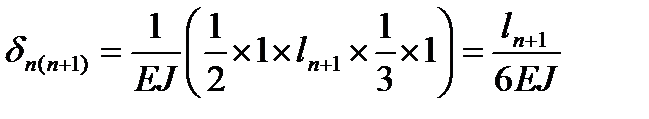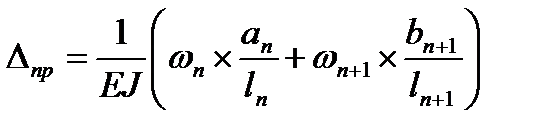На грузовой эпюре М_р (рис. 9.33, д):

ω₁, ω_п+1 – площадь грузовой эпюры;

а_п, а_п+1 – расстояние от центра тяжести эпюры до левой опоры пролета;

b_п, b_п+1 – расстояние от центра тяжести эпюры до правой опоры пролета.

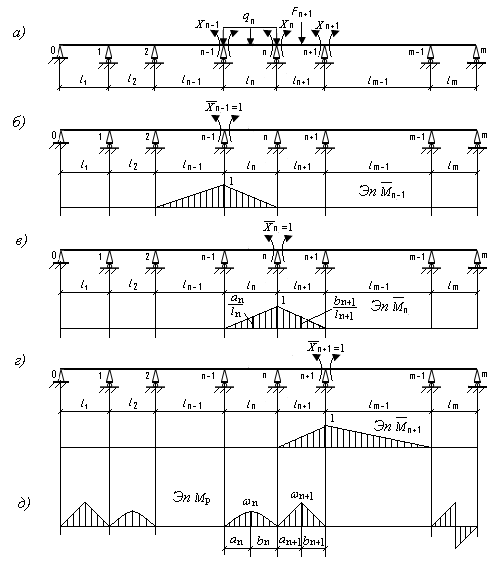
Рис. 9.33. Схема для решения уравнения совместности деформаций

для n-й опоры неразрезной балки

Подставив найденные коэффициенты и свободный член в уравнение совместности деформаций для n-й опоры и учитывая, что М₁ = х₁; М₂ = х₂; …; М_п = х_п, получим уравнение трех моментов:

М_п–1l_n + 2 М_п(l_n + l_n+1) + M_n+1l_n+1 = –6R_n^ф,

где 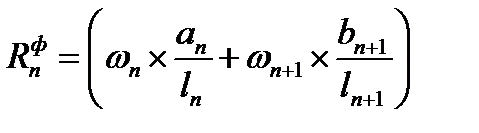– фиктивная реакция на п-йопоре.

Уравнения трех моментов составляют, продвигаясь по балке слева направо для пары пролетов. Следующее уравнение составляют, продвигаясь на один пролет вправо. В итоге получается система стольких уравнений, сколько раз неразрезная балка является статически неопределимой.

В каждой системе неизвестными являются опорные моменты над промежуточными опорами. Моменты над крайними опорами всегда известны (равны нулю или создаются внешней нагрузкой, приложенной на консоли).

Решение системы уравнений выполняется методом последовательного исключения неизвестных.

Если в пролете эпюра М_р имеет сложную форму, то она разбивается на простые составляющие, и фиктивная реакция определяется способом Верещагина как алгебраическая сумма составляющих, с учетом знака площади каждой части эпюры.

Если левый или правый конец балки защемлен, то для удобства составления уравнений трех моментов заделку заменяют дополнительным пролетом нулевой длины.

Для определения деформаций балки при изгибе можно использовать способ сравнения деформаций, который рассмотрим на конкретном примере (рис. 9.34, а).

Выполняем решение уравнения совместности деформаций у_В = 0. Прогиб точки B в основной системе, под действием равномерно распределенной нагрузки q и опорной реакции R_В, складывается из двух прогибов: одного, вызванного лишь нагрузкой q, и другого, вызванного опорной реакцией R_В (рис. 9.34, б, в).

Таким образом,

у_В = y_q + y_RB = 0.

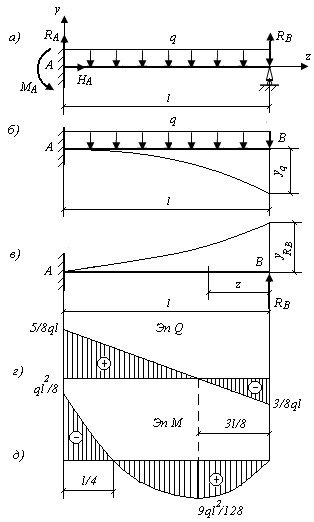
Рис. 9.34. Схема балки для определения перемещений

способом сравнения деформаций

Определим эти прогибы:

;

;

,

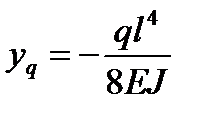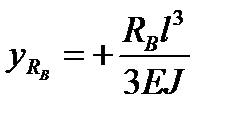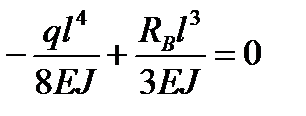отсюда

.

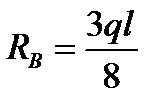Подставим значение лишней реакции R_В в уравнения статики для заданной системы (рис. 9.34, а), получим:

;

.

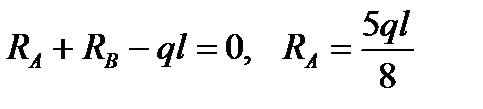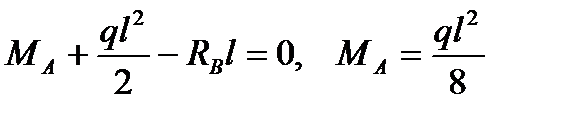Составим общие уравнения моментов и поперечных сил для правой части балки (рис. 9.34, а):

;

.

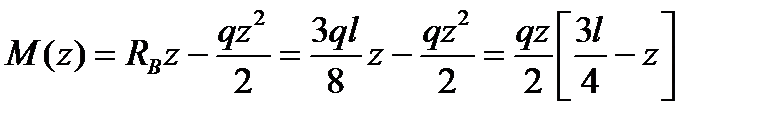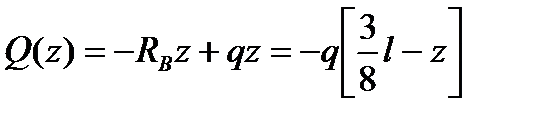Определим ординату z, при которой изгибающий момент в правой части балки принимает экстремальное значение:

,

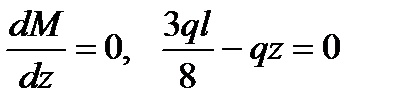отсюда

.

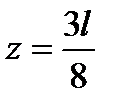Таким образом,

.

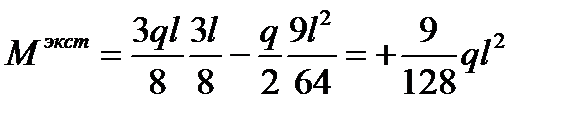Эпюры моментов и поперечных сил изображены на рис. 9.34, г, д.

Пример расчета

Задача 1.Для балки, изображенной на рис. 9.35, а, построить эпю-ры поперечных сил и изгибающих моментов.

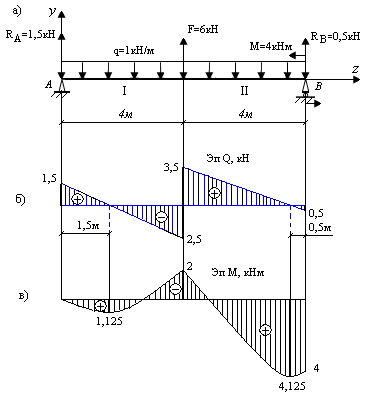
Рис. 9.35. Схема построения эпюр Q и M

для однопролетной балки

Решение.

1. Определим опорные реакции:

;

.

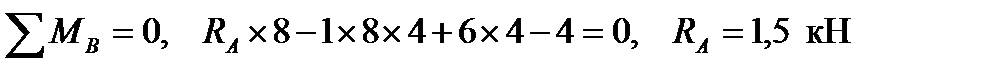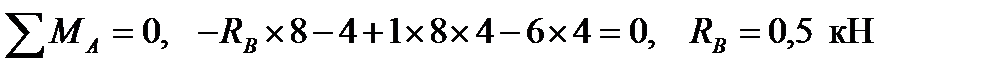2. Выполним проверку:

,

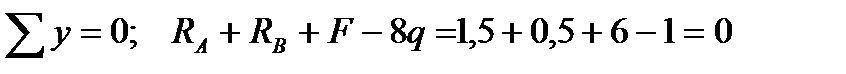реакции определены верно.

3. Разбиваем балку на участки (рис. 9.35, а).

4. Составим общие уравнения Q и М для каждого участка балки. Обходим балку слева направо:

1-й участок: 0 ≤ z₁ ≤ 4 м;

;

.

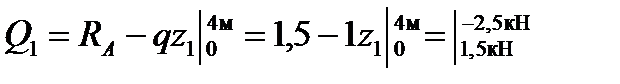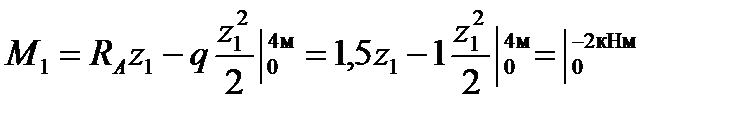Определим экстремальное значение момента на 1-м участке:

Q₁ = R_A – qz₁ = 1,5 – 1z₁ = 0, z₁ = 1,5 м;

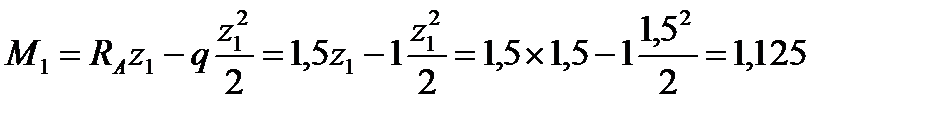кНм.

Обходим балку справа налево:

2-й участок: 0 ≤ z₂ ≤ 4 м;

;

.

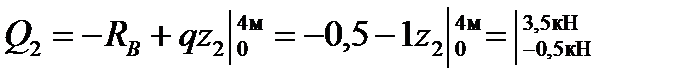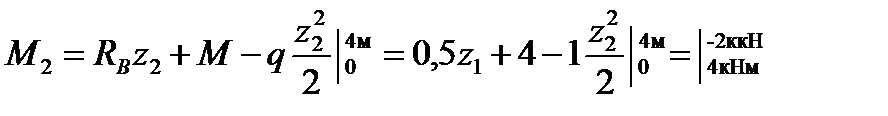Определим экстремальное значение момента на 2-м участке:

Q₂ = –R_В + qz₂ = –0,5 + 1z₂ = 0, z₂ = 0,5 м;

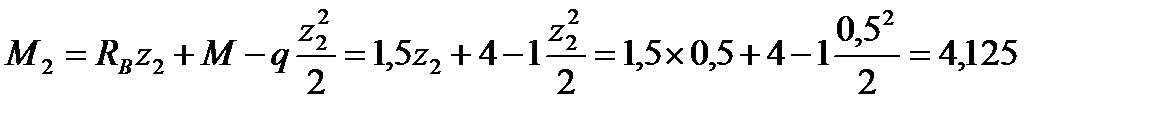кНм.

5. По полученным значениям ординат строим окончательные эпюры Q и M (рис. 9.35, б, в).

Задача 2. Для балки, изображенной на рис. 9.36, а, построить эпюры поперечных сил и изгибающих моментов.

Решение.

1. Определим опорные реакции:

;

.

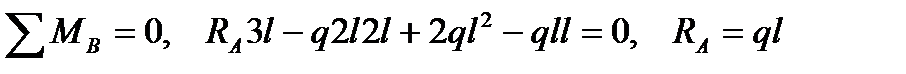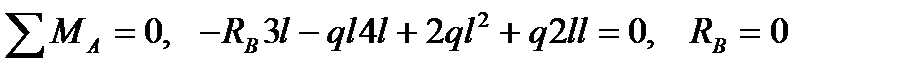2. Выполним проверку:

,

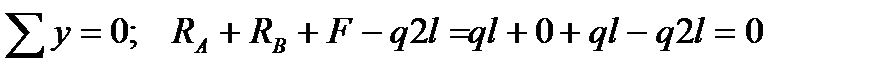реакции определены верно.

3. Разбиваем балку на участки (рис. 9.36, а ).

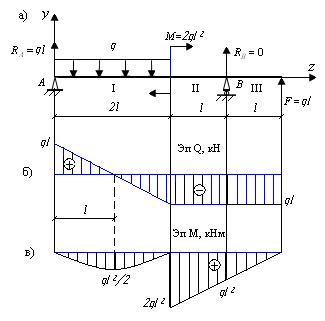
Рис. 9.36. Схема построения эпюр Q и M

для однопролетной балки

4. Составим общие уравнения Q и M для каждого участка балки. Обходим балку слева направо:

1-й участок: 0 ≤ z₁ ≤ 2l;

;

.

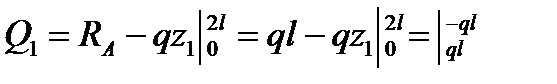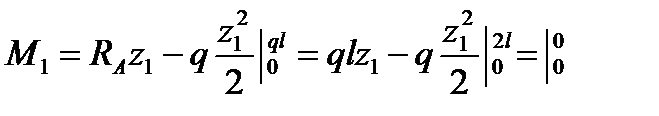Определим экстремальное значение момента на 1-м участке:

Q₁ = R_A – qz₁ = ql – qz₁ = 0, z₁ = l м;

.

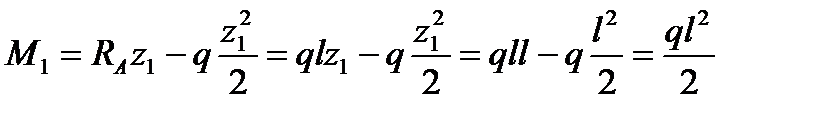2-й участок: 0 ≤ z₂ ≤ l;

;

.

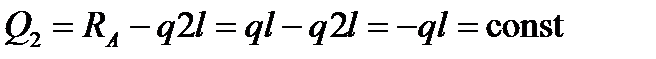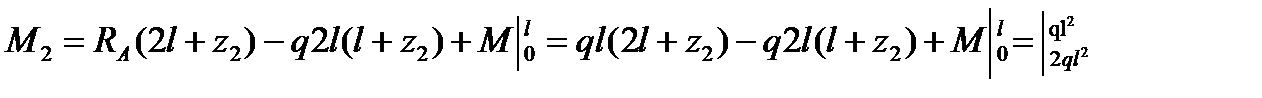Обходим балку справа налево:

3-й участок: 0 ≤ z₃ ≤ l;

Q₁ = –F = –const;

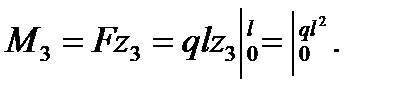
5. По полученным значениям ординат строим окончательные эпюры Q и M (рис. 9.36, б, в).

Задача 3.Для балки, изображенной на рис. 9.37, а, построить эпюры поперечных сил и изгибающих моментов.

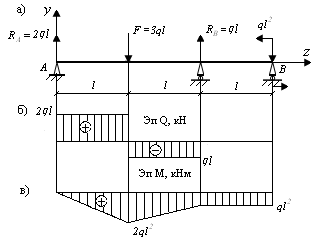
Рис. 9.37. Схема построения эпюр Q и M

для однопролетной балки

Решение.

По аналогии с решениями предыдущих задач определяем орди-наты эпюр Q и M. Окончательные эпюры Q и M изображены на рис. 9.37, б, в.

Задача 4.Проверить прочность балки таврового сечения при [σ]_р = 30 МПа и [σ]_сж = 60 МПа (рис. 9.38, а).

Решение.

1. Определим координаты центра тяжести таврового сечения относительно оси, проходящей по нижнему основанию сечения (рис. 9.38, б):

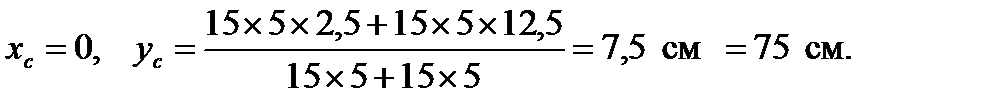
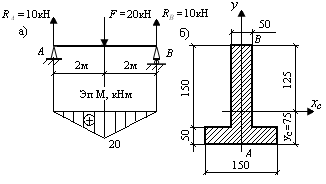
Рис. 9.38. Схема однопролетной балки для расчета на прочность

2. Определим осевой момент инерции таврового сечения относительно оси x_c:

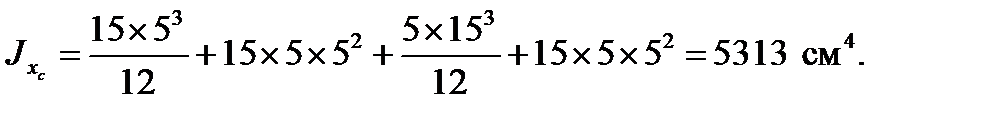
3. Определим моменты сопротивления таврового сечения в сечениях, наиболее удаленных от оси x_c:

- растянутая зона

;

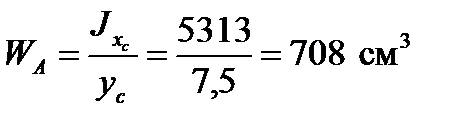- сжатая зона

.

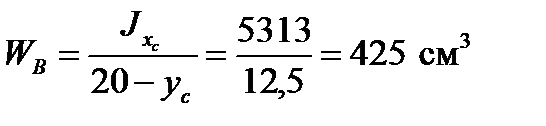4. Определим максимальный изгибающий момент в поперечных сечениях балки:

.

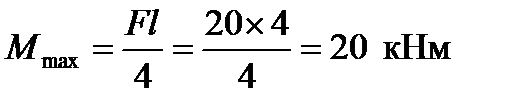5. Определим нормальные напряжения в сечениях А и B:

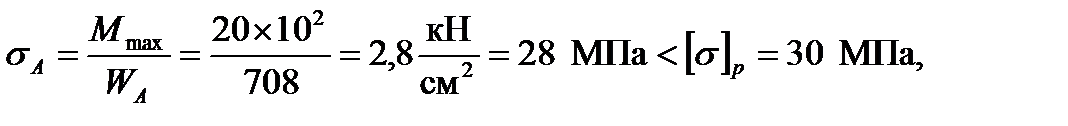
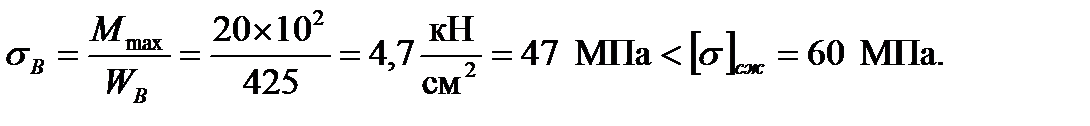
Условие прочности соблюдается.

Задача 5.Для заданной схемы нагружения балки (рис. 9.39, а) подобрать прямоугольное сечение, [σ] = 200 МПа.

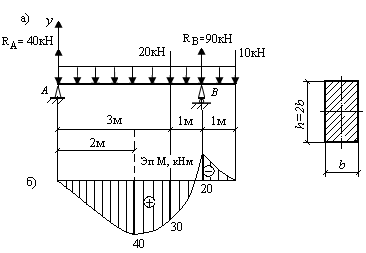
Рис. 9.39. Схема однопролетной балки для определения

размеров сечения

Решение.

1. Определим опорные реакции:

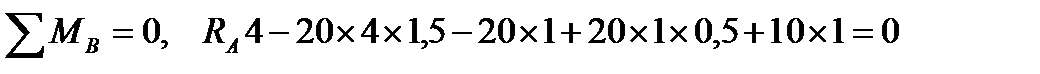, R_A = 40 кН;

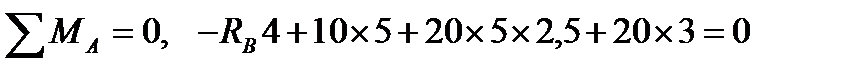, R_В = 90 кН.

2. Строим эпюру изгибающих моментов, которая изображена на рис. 9.39, б. По эпюре определяем значение M_max = 40 кНм.

3. Из условия прочности находим момент сопротивления прямоугольного сечения:

,

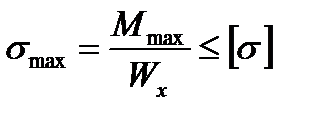откуда ,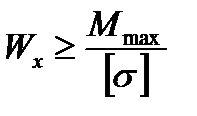

далее ;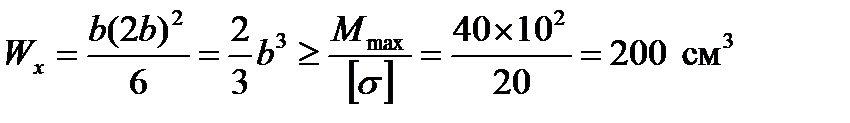

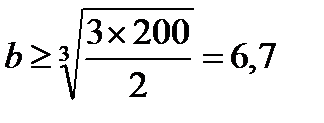см,

окончательно b = 6,7 см, h = 2b = 13,4 см.

Задача 6.Для балки, изображенной на рис. 9.40, а, подобрать сечение, состоящее из двух швеллеров, [σ] = 160 МПа.

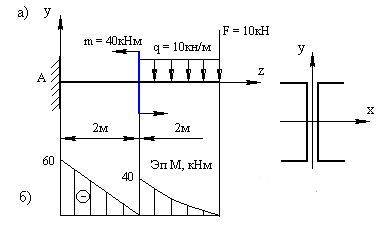
Рис. 9.40. Схема консольной балки

для подбора поперечного сечения

Решение.

1. Строим эпюру изгибающих моментов, двигаясь по балке от конца консоли к заделке (рис. 9.40, б). М_max = 60 кНм.

2. Из условия прочности определим момент сопротивления составного сечения балки:

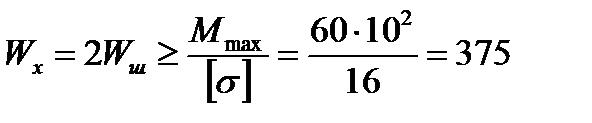см³,

откуда W_ш = 188 см³.

По ГОСТ 8240–72 подбираем швеллер № 22 с моментом сопротивления W_х = 192 см³.

Задача 7.Двутавровая балка № 36 загружена, как указано на рис. 9.41, а. Определить допускаемую грузоподъемность балки, если [σ] = 160 МПа.

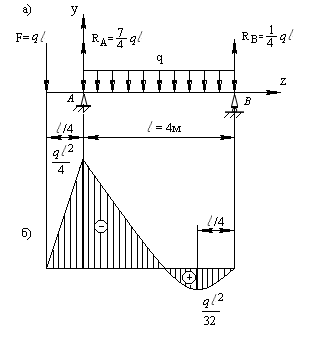
Рис. 9.41. Схема двутавровой балки для расчета

допускаемой грузоподъемности

Решение.

1. По ГОСТ 8239–72 для двутавра № 36 W_х = 743 см³.

2. Из условия прочности

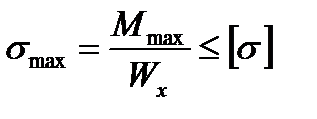
определим

,

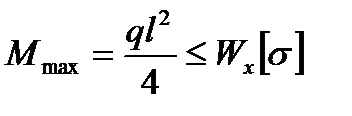тогда 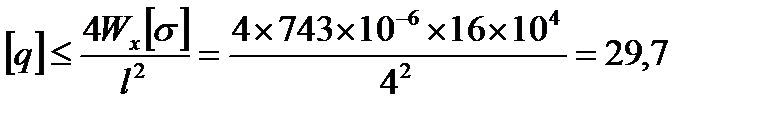кН/м,

[F] = [q]l = 29,7 ´ 4 = 118,9 кН.

Задача 8.Интегрированием дифференциального уравнения изогнутой оси балки, изображенной на рис. 9.42, определить прогиб и угол поворота конца консоли.

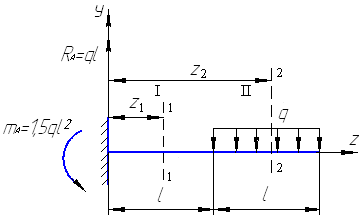
Рис. 9.42. Схема консольной балки для определения

перемещений

Решение.

1. Определим опорные реакции в заделке:

;

.

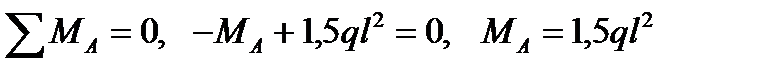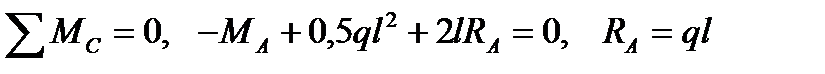2. Разобьем балку на участки (рис. 9.42) и составим уравнения упругой линии для каждого из них:

1-й участок:

,

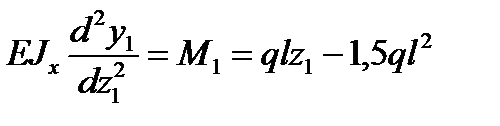проинтегрируем дважды это уравнение, получим:

;

.

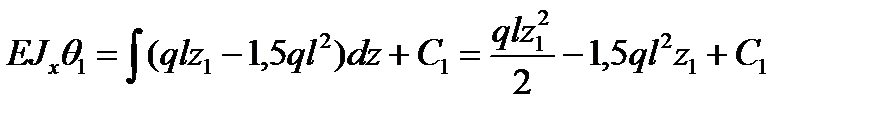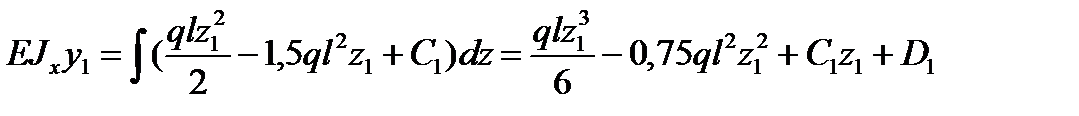2-й участок:

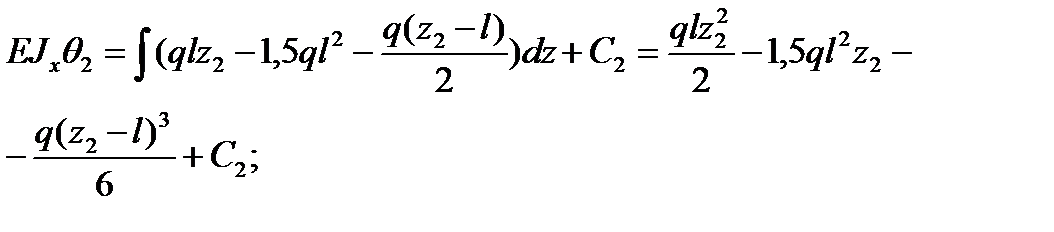
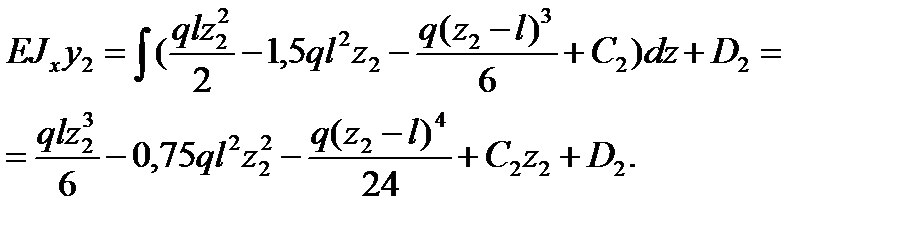
Рассмотрим начальные условия:

при z₁ = l = z₂; θ₁ = θ₂; С₁ = С₂ = С;

при z₁ = l = z₂; у₁ = у₂; D₁ = D₂ = D;

при z₁ = 0; θ₁ = 0; С = 0;

при z₁ = 0; у₁ = 0; D = 0.

Тогда последние два уравнения принимают вид:

;

,

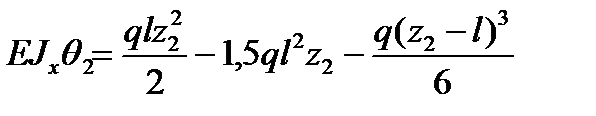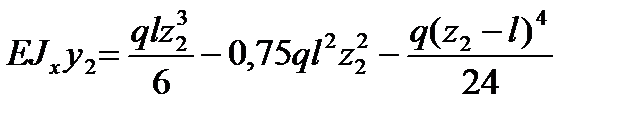тогда при z₂ = 2l; ;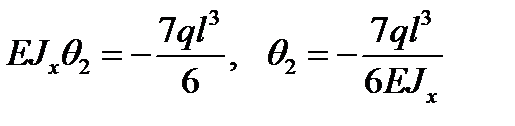

.

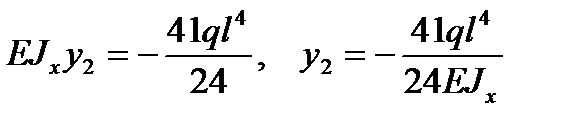9.14. Контрольные вопросы

1. Что такое чистый изгиб, поперечный изгиб и продольно-поперечный изгиб?

2. Внутренние силовые факторы при изгибе.

3. Как определяются нормальные и касательные напряжения при изгибе?

4. Построение эпюр М и Q при изгибе.

5. Дифференциальное уравнение изогнутой оси балки.

6. Условие прочности и жесткости при изгибе.

7. Рациональное сечение балки при изгибе.

8. Формула Журавского для определения касательных напряжений при изгибе.

9. Построение эпюр М и Q для простейших сечений при изгибе.

10. Определение перемещений при изгибе – аналитический, графоаналитический методы.

11. Метод начальных параметров.

12. Уравнение трех моментов при расчете неразрезных балок.

Кручение