Дифференциальное уравнение изогнутой оси балки

При поперечном изгибе ось балки принимает вид кривой, расположенной в плоскости действия внешних нагрузок. При этом точки оси получают поперечные перемещения у, а поперечные сечения совершают повороты относительно своих нейтральных осей на угол θ, равный углам наклона касательной и изогнутой оси балки (рис. 9.22).

Прогибы и углы поворотов поперечных сечений в балках являются функциями координаты z. Их определение необходимо для расчета балки на жесткость.

Рассмотрим изгиб балки в одной из главных плоскостей, например, в плоскости yz. Как показывает практика, элементы сооружений испытывают незначительные деформации (y_max/l = 10^-2…10^-3, где y_max - максимальный прогиб; l - пролет балки).

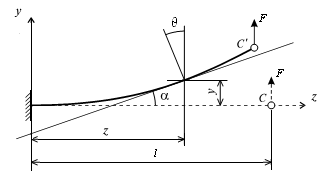
Рис. 9.22. Схема кривой оси балки при поперечном изгибе

В данном случае неизвестными функциями, определяющими положение точек поперечных сечений балки, являются y (z) и θ (z) = a (z). Из геометрических построений (рис. 9.22) видно, что угол наклона касательной к оси z и угол поворота поперечного сечения при произвольном значении z равны между собой. В силу малости углов поворота сечений имеем:

θ (z) ≈ tg θ (z) = y′ (z).

Из курса высшей математики известно, что кривизна плоской кривой y (z) выражается формулой

.

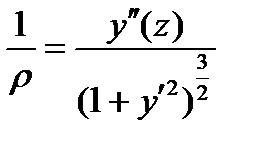Если в последнем выражении отбросить величину второго порядка малости, то с учетом формулы

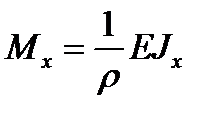
после несложных математических преобразований получим дифференциальное уравнение изогнутой оси балки:

,

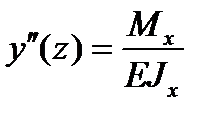где J_x – момент инерции поперечного сечения балки относительно ее

нейтральной оси;

Е - модуль упругости материала;

EJ_x - жесткость балки.

Данное уравнение в общем случае справедливо для чистого изгиба балки, т. е. когда изгибающий момент M_x имеет постоянное значение, а поперечная сила Q_y равна нулю. Это уравнение используется и в случае поперечного изгиба, при котором искривлениями поперечных сечений за счет их сдвигов пренебрегаем (гипотеза плоских сечений).

Введем еще одно упрощение, связанное с углом поворота поперечного сечения. Если изогнутая ось балки является пологой кривой, то углы поворота сечений можно принимать равными первой производной от прогибов. Отсюда следует, что прогиб балки принимает экстремальные значе­ния в тех сечениях, где угол поворота равен нулю.

В общем случае для того чтобы найти функции прогибов y (z) и углов поворота j (z), необходимо решить последнее уравнение с учетом граничных условий между смежными участками.

Для балки, имеющей несколько участков, определение формы упругой линии является достаточно сложной задачей, так как уравнение изогнутой оси балки, записанное для каждого участка, после интегрирования содержит две произвольные постоянные.

На границах соседних участков прогибы и углы поворота сечений являются непрерывными функциями. Это позволяет определить необходимое число граничных условий для вычисления произвольных постоянных интегрирования.

9.10. Способы определения перемещений при изгибе

Метод непосредственного интегрирования дифференциального уравнения упругой линии балки.

Уравнение 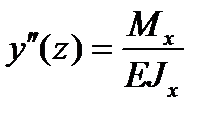дает возможность вычислить линейные и угловые перемещения сечений. Первое интегрирование дифференциального уравнения определяет закон изменения углов поворота сечений по длине балки:

.

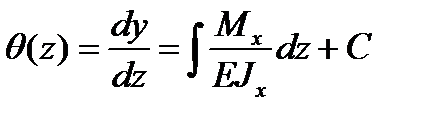Второе интегрирование полученного выражения позволяет определить функции прогибов точек упругой линии по длине балки:

.

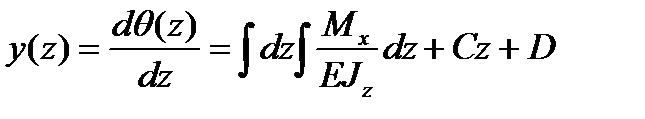При вычислении интегралов сначала составляем аналитические выражения изгибающего момента и жесткости в зависимости от координаты сечения z, в котором определяются перемещения. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления балки. Для однопролетной балки прогибы над опорами равны нулю. Для защемленной в опорном сечении балки прогиб и угол поворота равны нулю.

Рассмотрим пример. Найти перемещения консоли постоянного сечения, загруженной на свободном конце силой F (рис. 9.23).

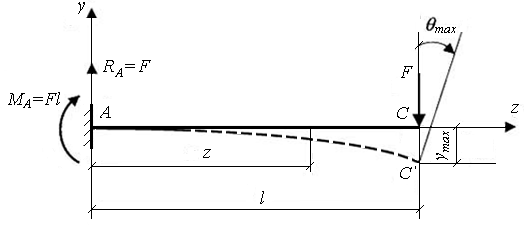
Рис. 9.23. Схема консольной балки, загруженной на свободном конце

силой F

В заделке возникает вертикальная реакция R_A = F и изгибающий момент М_A = Fl. Начало координат поместим на левом конце балки. Изгибающий момент в произвольном сечении, расположенном на расстоянии z от начала координат, определяется по формуле

M(z) = R_Az – M_A = Fz – Fl,

далее с учетом уравнения упругой линии имеем:

.

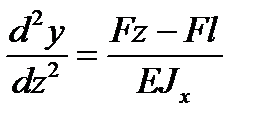Если жесткость балки – величина постоянная, то интегрируя уравнение упругой линии, получим:

;

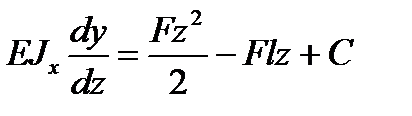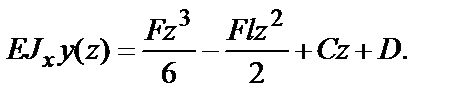
Для нахождения постоянных интегрирования С и D используем граничные условия.

При z = 0 (левый конец балки – заделка) угол поворота и прогиб равны нулю, тогда

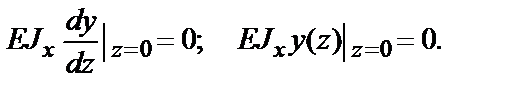
Подставляя эти значения в интегралы, находим, что С = D = 0,
тогда

;

.

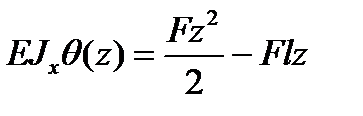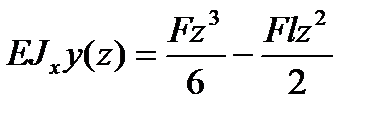Определим максимальные значения перемещений:

;

.

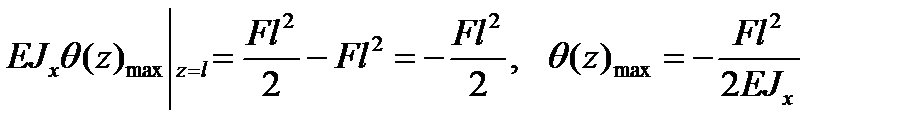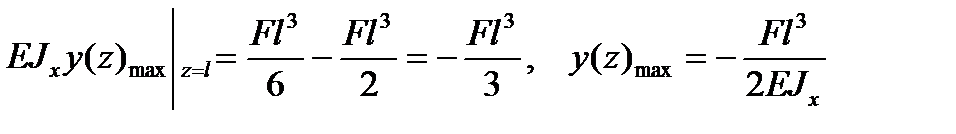Знак «минус» в формуле угла поворота свидетельствует о том, что поворот сечения происходит по часовой стрелке, знак «минус» в формуле прогиба указывает на то, что прогиб происходит вниз (не совпадает с положительным направлением оси у).

Если балка по условиям нагружения разбивается на п участков, то из условий непрерывности и плавности упругой линии необходимо составить и решить систему 2п уравнений. Совместное решение системы уравнений позволит найти постоянные интегрирования и получить для каждого участка уравнения прогибов и углов поворота. Необходимость совместного решения системы уравнений осложняет задачу, поэтому непосредственное интегрирование применяют только в тех случаях, когда число участков невелико (один, максимум два).

Метод начальных параметров.

Рассмотрим балку постоянной жесткости, загруженную положительными сосредоточенными моментами, силами и равномерно распределенной нагрузкой. Они считаются положительными, если вызывают в сечении положительный изгибающий момент (рис. 9.24).

Начало координат возьмем на левом конце балки, ось z направим вправо, ось у – вверх. Разобьем балку на ряд участков.

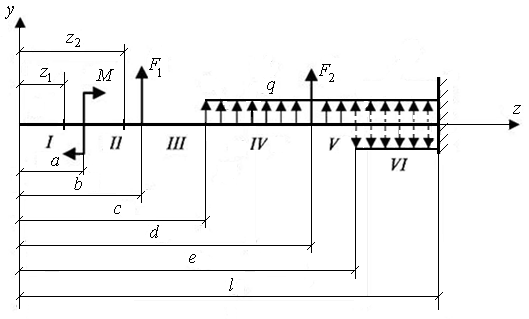
Рис. 9.24. Схема к расчету балки методом начальных параметров

Первый участок:

0 ≤ z₁ ≤ α; М(z) = 0,

тогда

,

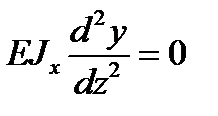проинтегрируем уравнение упругой линии, получим:

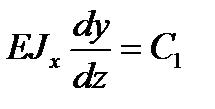; EJ_xy(z) = C₁z + D₁.

Второй участок:

α ≤ z₂ ≤ b, M(z) = M.

Умножим изгибающий момент на величину (z₂ – a)⁰, равную единице:

M(z) = M(z₂ – α)⁰;

,

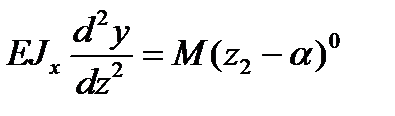после интегрирования имеем:

.

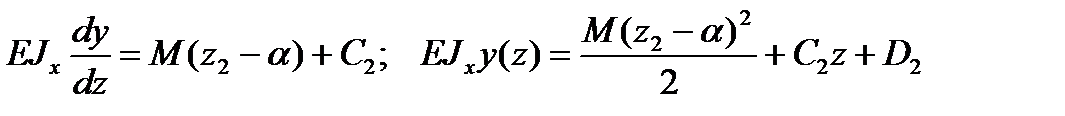Постоянные интегрирования определим из условия, что упругая линия не имеет разрывов и изломов и является плавной кривой. На границе первого и второго участков имеем:

,

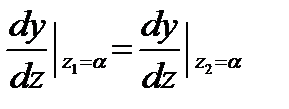для п участков балки получим: С₁ = С₂ = … = С_п = С;

,

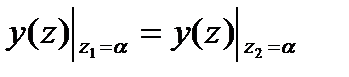тогда для п участков балки: D₁ = D₂ =…= D_n = D.

Определим физический смысл постоянных интегрирования С и D. Если обозначить угол поворота и прогиб в начале координат через θ₀и у₀, то из уравнения упругой линии получим:

С = EJ_xθ₀; D = EJ_xy₀ – начальные параметры.