Нормальные напряжения при изгибе. Эпюры напряжений

В сечении балки, взятом на участке чистого изгиба, возникает только один изгибающий момент

.

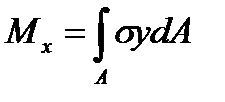Следовательно, в сечении действуют нормальные напряжения σ (рис. 9.3).

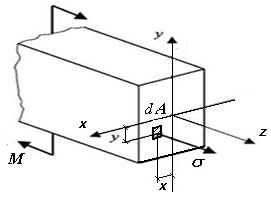
Рис. 9.3. Схема внутренних сил при чистом изгибе

Продольная сила N и изгибающий момент М_у будут равны нулю, т. е.

;

.

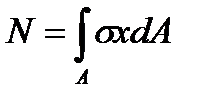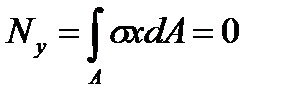Из формулы для определения изгибающего момента М_х нельзя определить величину нормальных напряжений σ, так как неизвестно, как они распределены по сечению.

Задача определения напряжений σ в сечении балки является статически неопределимой. Пусть отдельное волокно при изгибе испытывает простое растяжение или сжатие. Тогда для него можно записать закон Гука как при растяжении:

σ = Еε.

Чтобы найти относительную деформацию ε на участке чистого изгиба, выделим элемент балки длиной dz и рассмотрим его деформацию.

Сечения mn и m₁n₁ остаются плоскими и поворачиваются на угол dφ/2. Волокна нейтрального слоя искривляются, но их длина не изменяется. Радиус кривизны нейтрального слоя обозначим ρ. Тогда имеем:

dz = OO₁ = ρdφ.

Волокно АВ, расположенное на расстоянии у от нейтрального слоя, удлиняется, радиус его кривизны составляет ρ + у (рис. 9.4).

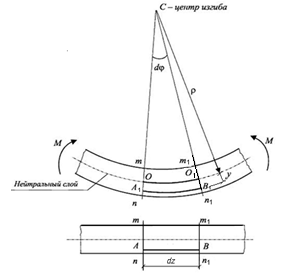
Рис. 9.4. Схема деформации элемента балки длиной dz

Относительное удлинение волокна:

.

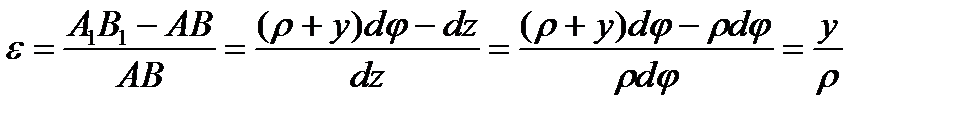Тогда .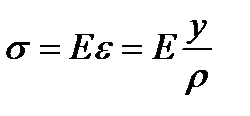

Подставим данное выражение в формулу для М_х:

.

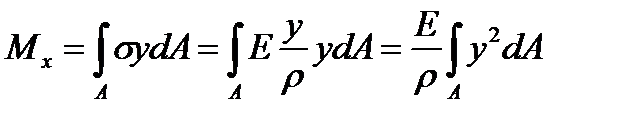Учитывая, что

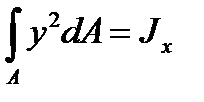
представляет момент инерции сечения относительно оси x, можно записать

.

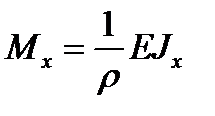Откуда

.

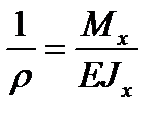Величина EJ_x называется жесткостью поперечного сечения при изгибе.

Из вышеприведенной формулы видно, что если балка изготовлена из однородного материала(Е = const) и имеет постоянное сечение (J_x = const), то при чистом изгибе (М = const) ее ось искривляется по дуге окружности (ρ = const). Подставим в формулу для определения σ значение кривизны, получим:

.

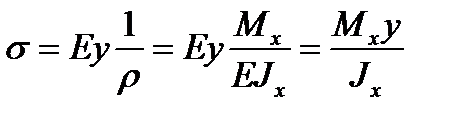Из формулы видно, что нормальные напряжения распределяются по сечению неравномерно и достигают наибольшего значения в точках, наиболее удаленных от нейтральной оси. При положительном изгибающем моменте нижние волокна будут растянуты (ρ > 0), а верхние волокна сжаты (ρ < 0).

Определим положение нейтральной оси сечения z. Для этого приравняем к нулю N и М_y:

;

.

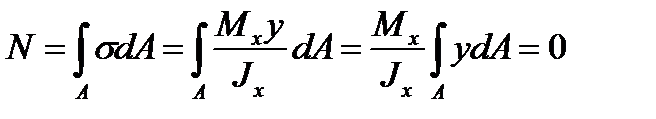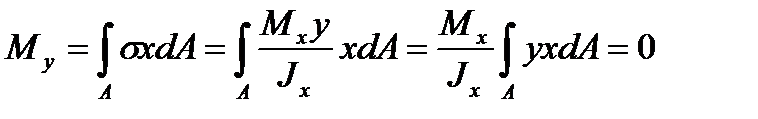Так как

,

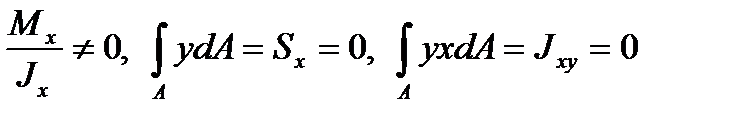то на основании этого делаем заключение, что нейтральная ось z проходит через центр тяжести сечения, а оси x и у являются главными центральными осями сечения. Эпюра напряжений для сечений, имеющих горизонтальную ось симметрии, всегда будет иметь вид, представленный на рис. 9.5.

При положительном изгибающем моменте все волокна, расположенные выше нейтральной линии, являются сжатыми, а ниже ее – растянутыми.

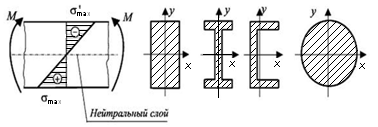
Рис. 9.5. Эпюра распределения нормальных напряжений в сечениях

с горизонтальной осью симметрии

Максимальные нормальные напряжения возникают при у = у_max. Таким образом,

.

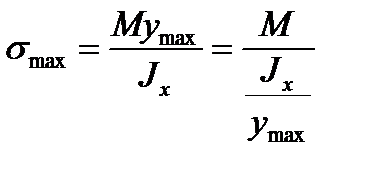Отношение осевого момента инерции к расстоянию от наиболее удаленной точки сечения до нейтральной оси называется осевым моментом сопротивления, т. е.

.

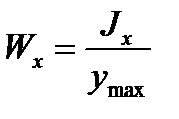Момент сопротивления измеряется в сантиметрах кубических (см³) и зависит от формы и размеров поперечного сечения, тогда

.

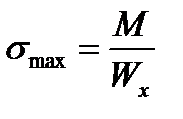Если сечение не имеет горизонтальной оси симметрии (рис. 9.6), то расстояния от нейтральной оси до крайних нижних и крайних верхних волокон различны.

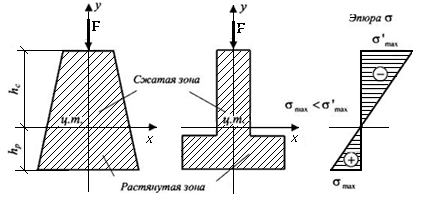
Рис. 9.6. Эпюра распределения нормальных напряжений

в сечениях без горизонтальной оси симметрии

Обозначим их через h_p и h_ссоответственно. Тогда напряжения в крайних волокнах выразятся формулами:

; .

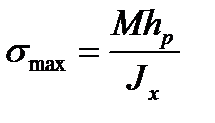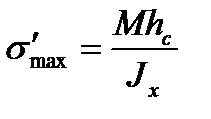9.3. Построение эпюр изгибающего момента М

и поперечной силы Q при изгибе

При расчете балок на изгиб необходимо знать законы распределения внутренних усилий в поперечных сечениях и уметь строить эпюры внутренних силовых факторов.

Рассмотрим три основных типа опорных связей балки.

1. Шарнирно-неподвижная опора (рис. 9.7, а- левая опора балки), ограничивающая горизонтальное и вертикальное перемещение опорной связи и лишающая систему двух степеней свободы.

2. Шарнирно-подвижная опора (рис. 9.7, а - правая опора балки), ограничивающая вертикальное перемещение опорной связи и лишающая систему одной степени свободы.

3. Жесткая заделка (рис. 9.7, б), не допускающая поворота и перемещений по вертикали и горизонтали сечения балки, примыкающего к опоре и лишающая систему трех степеней свободы.

Рассмотрим построение эпюр М и Q на конкретном примере (рис. 9.7, а). Решение задачи начинаем с вычерчивания расчетной схемы, приложив к балке внешние активные и реактивные силы. Заданная система является статически определимой, следовательно, из условий равенства нулю суммы моментов всех сил относительно шарнирных закреплений определяем вертикальные реакции в опорах:

;

.

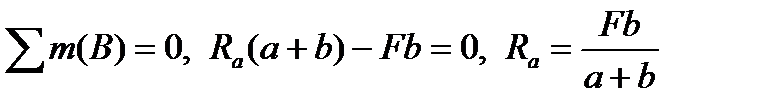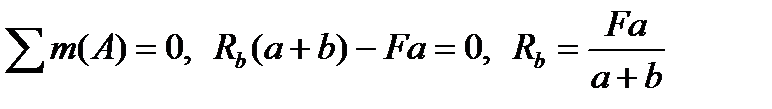Для определения реакции Н_А имеем:

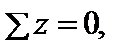откуда Н_А = 0.

Для проверки правильности вычислений воспользуемся условием равенства нулю суммы всех вертикальных сил Sу = 0, откуда получим:

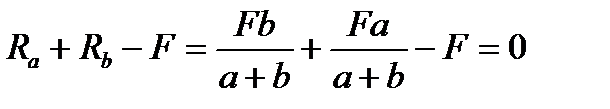, реакции найдены верно.

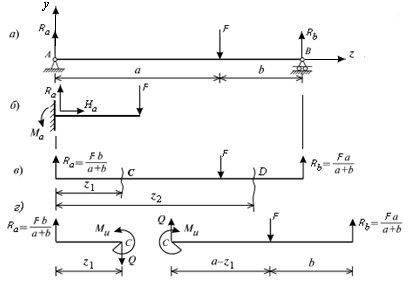
Рис. 9.7. Расчетная схема однопролетной балки

Для определения внутренних силовых факторов (изгибающего момента М(z) и поперечной силы Q(z)), как функций от продольной координаты z, воспользуемся методом сечений. Для получения этих зависимостей разбиваем балку на участки, границами которых являются следующие сечения: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенной нагрузки; сечения, в которых скачкообразно изменяется жесткость балки; точки, где происходит изменение положения элементов стержневой системы со сложной структурой.

Заданная балка (рис. 9.7, в) состоит из двух участков - первого (0 £ z₁£ a) и второго (a £ z₂ £ a + b). Рассматривая последовательно сечения, принадлежащие к первому и второму участкам, и равновесие отсеченных частей балки при действии на них всех внешних сил и внутренних усилий, составим общие уравнения для внутренних силовых факторов.

В системе координат y0z, принятой на рис. 9.8, а, положительный момент вызывает растяжение нижних волокон балки. При построении эпюры М(z) положительные ординаты откладываются вниз от нулевой линии, отрицательные – вверх.

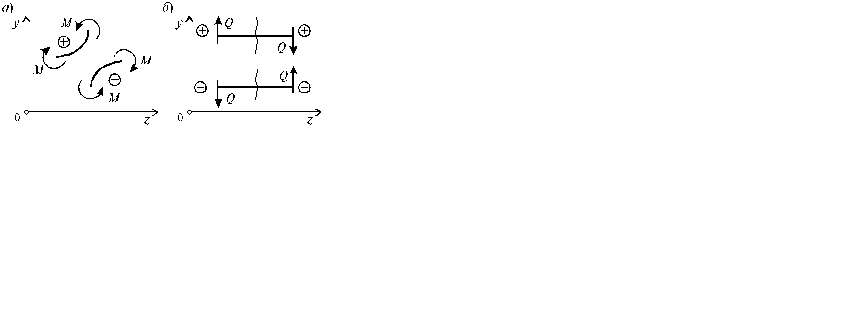
Рис. 9.8. Правило знаков для изгибающих моментов

и поперечных сил

Для поперечных сил, независимо от направления координатных осей, устанавливается следующее правило знаков: если результирующая поперечная сила Q_y вращает рассматриваемую часть балки по ходу часовой стрелки, то она считается положительной, в противном случае - отрицательной (рис. 9.7, б). При построении эпюры Q(z) положительные ординаты откладываются вверх от нулевой линии, отрицательные – вниз.

Из условия равновесия SM_x = 0; Sy = 0 отсеченной части балки (рис. 9.7, г), расположенной левее от сечения z₁ (первый участок), имеем:

M_x (z₁) = R_a z₁; Q_y = R_a.

Для определения M_x и Q_y на втором участке рассмотрим равновесие отсеченной части балки, расположенной правее от сечения z₂ (рис. 9.7, г), т. е. SM_x = 0; Sy = 0, откуда

M_x (z₂) = R_b (a + b - z₂); Q_y = -R_b.

Эпюры M_x и Q_y построены на растянутых волокнах и изображены на рис. 9.9.

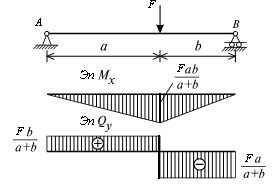
Рис. 9.9. Построение эпюр М_х и Q_у при изгибе