Внешние силы и их классификация

Все конструкции машин и инженерные сооружения в процессе эксплуатации находятся в постоянном взаимодействии между собой и с внешней средой. Силы взаимодействия отдельных элементов с внешней средой или соседними элементами называются внешними силами. Если они известны в начальной стадии расчета, то их называют активными силами или нагрузками, если не известны – их называют реактивными силами или просто реакциями.

На основании аксиомы связей реакции связей можно рассматривать как внешние силы. Внешние силы можно классифицировать по нескольким основным признакам.

1. По способу передачи на тело:

а) поверхностные силы, которые передаются на тело через поверхность (давление газов в цилиндрах, давление грунта на нож скрепера, грейдера или бульдозера);

б) объемные силы, которые передаются на тело через объем (собственный вес, магнитные силы, силы инерции);

в) распределенные силы, которые непрерывно распределены по некоторой части поверхности. Их величина задается интенсивностью;

г) сосредоточенные силы, которые передаются на тело по небольшой части поверхности. Для упрощения их действие заменяют действием равнодействующей, которую называют сосредоточенной силой. Аналогично вводится понятие сосредоточенной пары сил или момента.

2. По характеру действия во времени:

а) статические – силы, медленно изменяющиеся во времени, не вызывающие существенных сил инерции;

б) динамические – силы, быстро изменяющиеся во времени, вызывающие большие силы инерции, которые необходимо учитывать в расчетах. Динамические силы могут быть ударными, внезапно приложенными и вибрационными;

в) повторно-переменные – силы, действия которых периодически повторяются многократно.

3. По длительности действия во времени:

а) постоянные силы, которые действуют на элемент конструкции в процессе эксплуатации (собственный вес, вес оборудования и т. п.);

б) временные силы, которые действуют на элемент конструкции в течение определенного промежутка времени (вес поезда или автомобиля на мосту, вес монтажного оборудования и т. д.).

1.5. Основные гипотезы и принципы механики материалов

Для упрощения решения практических задач в механике материалов приняты следующие основные упрощающие гипотезы, касающиеся в основном свойств материала.

Гипотеза сплошности. Предполагается, что материал заполняет форму тела сплошным образом и эта сплошность не нарушается под действием внешних воздействий и деформации тела.

Гипотеза изотропности и однородности. В окрестности любой точки тела физико-механические свойства материала одинаковы во всех направлениях и не изменяются при переходе к другим точкам и по всему объему тела.

Гипотеза идеальной упругости и линейности деформирования. Деформации тела прямо пропорциональны действующим нагрузкам и полностью исчезают после снятия нагрузки.

Гипотеза малых деформаций. В механике материалов рассматривают только перемещения и деформации, величины которых малы по сравнению с размерами деформируемого тела. Это дает возможность пренебрегать изменением расположения внешних нагрузок при деформировании тел и составлять уравнения равновесия статики без учета этих изменений.

Приведем также общие принципы, на которых базируются расчеты в механике материалов.

Принцип независимости действия сил. Основывается на гипотезах об идеальной упругости материала и малых деформациях. Согласно этому принципу деформации и перемещения в любой точке тела, вызванные системой нагрузок, равны сумме деформаций и перемещений, вызванных каждой нагрузкой отдельно, и не зависят от порядка их приложения.

Принцип Сен-Венана. Предполагает, что если к телу приложена самоуравновешивающаяся система сил, то напряжения и деформации быстро убывают при удалении от места приложения нагрузки. Согласно этому принципу способ приложения нагрузки влияет только на деформацию тела в малом объеме, примыкающем к месту приложения нагрузки, и не влияет на деформацию тела вдали от точек ее приложения.

Принцип Сен-Венана широко используется при решении практических задач.

Принцип отвердения. Равновесие тела не нарушится, если предположить, что оно является абсолютно твердым. В соответствии с этим принципом при составлении уравнений равновесия можно пренебрегать деформациями тела.

На этих основных гипотезах и принципах базируется наука о механике материалов.

1.6. Контрольные вопросы

1. В чем заключаются цель и задачи механики материалов?

2. Что изучает наука о механике материалов?

3. Какие основные гипотезы используются в решении практических задач по механике материалов?

4. Что такое прочность, условия прочности при различных видах напряженно-деформированного состояния инженерных конструкций?

5. Что такое жесткость инженерных конструкций?

6. Что такое устойчивость инженерных конструкций?

7. Что такое расчетная схема?

8. Основные элементы инженерных конструкций.

9. Внешние силы, их классификация.

10. Основные виды опорных закреплений.

2. ВНУТРЕННИЕ СИЛЫ И УСИЛИЯ. МЕТОД СЕЧЕНИЙ

2.1. Понятие о внутренних силах и напряжениях

Из физики известно, что между частицами любого тела (атомами, молекулами, кристаллами) действуют силы взаимодействия, которые называются внутренними. Но в механике материалов под внутренними силами понимают только изменение этих сил, вызванное действием внешних сил. Поэтому в дальнейшем под внутренними силами будем понимать силы взаимодействия, возникающие между частицами или частями тела, при действии на него внешних сил. Величина внутренних сил определяет способность внешних сил разрушить тело. Поэтому для оценки прочности тела необходимо, прежде всего, знать их.

Для определения внутренних сил в механике материалов используют метод сечений. Суть его выясним на конкретном примере.

Рассмотрим стержень (рис. 2.1, а), находящийся в равновесии под действием внешних сил.

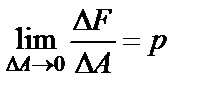Для определения внутренних сил в произвольной точке О проведем мысленно через эту точку поперечное сечение 1–1, которое разделит стержень на две части – А (левую) и В (правую). Мысленно отделим левую и правую части друг от друга (рис. 2.1, б). При этом равновесие каждой из них нарушится. Для того чтобы уравновесить внешние силы, приложенные к обеим частям стержня, необходимо в сечении 1–1 приложить уравновешивающие внутренние силы. Выделим в окрестности точки С элементарную площадку DА и обозначим через DF равнодействующую внутренних сил, приложенных к ней. Предел отношения называется полным напряжением. С физической точки зрения полное напряжение – интенсивность внутренних сил в точке, а с математической – вектор, модуль которого являет-

ся мерой внутренних сил в точке. Полное напряжение измеряется в единицах силы, отнесенной к площади (Н/м², кН/м², Па, МПа и т. д.).

Разложим вектор р на составляющие в прямоугольной системе координат ХОУZ (рис. 2.2). Начало системы координат совместим с центром тяжести поперечного сечения; ось Z направим вдоль оси стержня, a оси X и У совместим с осями симметрии сечения и назовем их главными центральными осями. Составляющая полного напряжения р, направленная вдоль нормали к сечению (ось Z), обозначается греческой буквой s и называется нормальным напряжением. Оно считается положительным, если направлено в сторону внешней нормали.

Составляющая полного напряжения р, расположенная в плоскости сечения, обозначается греческой буквой t и называется полным касательным напряжением. Напряжение t можно разложить на координатные составляющие t_zx и t_zy.Напряжение t_zx (t_zy) считается положительным, если при взгляде с положительного направления координатной оси y(x) оно вращает стержень относительно противоположного конца по часовой стрелке. На рис. 2.2 t_zx < 0,t_zy > 0.

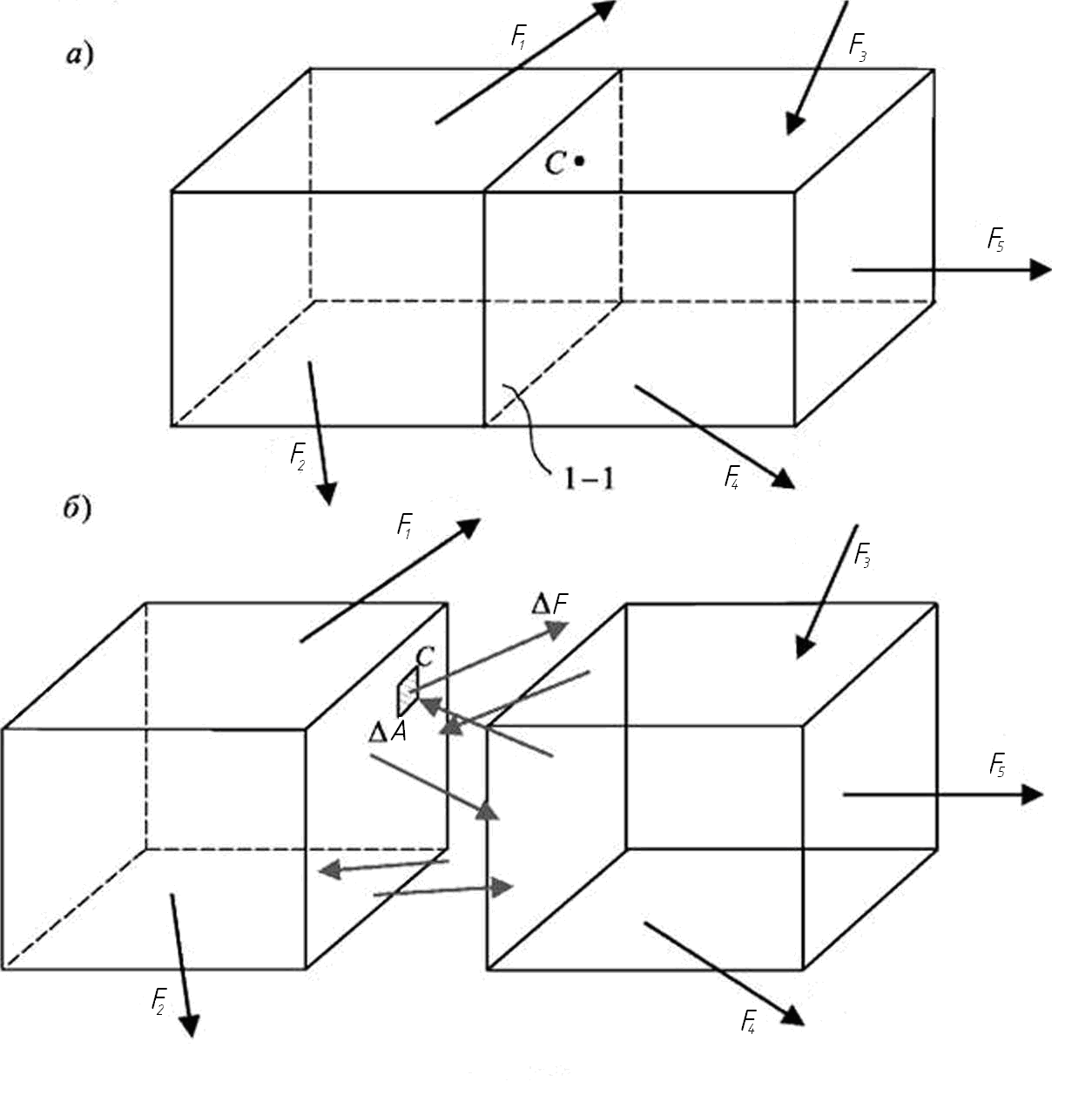
Рис. 2.1. Схема стержня с внешней нагрузкой, приложенной к нему

Рис. 2.2. Схема распределения в поперечном

сечении стержня напряжений

Полное напряжение на элементарной площадке dA определяется по формуле

;

ными (перерезывающими) силами;

– называется крутящим моментом

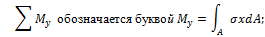
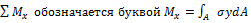– называется изгибающим моментом.

Проекции внутренних сил, действующих в поперечном сечении бруса, на координатные оси и моменты их относительно этих осей, т. е. N, – называются внутренними усилиями.

Продольная сила N – сумма проекций всех внутренних сил, действующих в поперечном сечении стержня, на его ось; поперечные силы 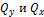– сумма проекций всех внутренних сил, действующих в поперечном сечении бруса на оси y и x соответственно. Знаки N, 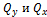совпадают со знаками 𝜎, соответственно.

2.2. Внутренние усилия

Спроектируем все внутренние силы, действующие в поперечном сечении стержня, на координатные оси и найдем моменты их относительно этих осей.

Крутящий момент – сумма моментов всех внутренних сил, действующих в поперечном сечении стержня, относительно его оси. М_кр > 0, если при взгляде со стороны внешней нормали он совершает вращение по часовой стрелке.

Изгибающие моменты М_у и М_х – сумма моментов всех внутренних сил, действующих в поперечном сечении стержня, относительно его главных центральных осей у и х соответственно. М_у > 0 и М_х > 0, если моменты изгибают стержень так,что его вогнутость располагается со стороны положительной координатной оси х и у соответственно.

Полученные выражения внутренних усилий через внутренние силы называют интегральными зависимостями. Из них нельзя определить внутренние силы, т. е. напряжения σ, τ_zу и τ_zx, так как неизвестен закон их распределения по сечению и значение внутренних усилий.

– называется продольной (осевой) силой.

Что касается внутренних усилий, то их всегда можно определить через внешние силы. В статически определимых конструкциях (системах) для этого достаточно воспользоваться условиями равновесия. Если для определения усилий в сечениях элементов условий равновесия недостаточно, то такие конструкции (системы) называются статически неопределимыми.

Следует отметить, что даже при известных внутренних усилиях определить напряжения из полученных интегральных зависимостей нельзя. Поэтому задача вычисления напряжений всегда является статически неопределимой.

2.3. Выражение внутренних усилий через внешние силы

Рассмотрим равновесие одной из частей стержня, например, левой (обычно рассматривается та часть стержня, на которую действует меньшее количество внешних сил).

На левую часть стержня действуют внешние силы F₁, F₂ и внутренние силы в поперечном сечении 1–1. Так как внутренние усилия являются равнодействующими внутренних сил, то их действие статически эквивалентно действию внутренних сил. Поэтому в сечении 1–1 можно приложить вместо внутренних сил положительные внутренние усилия (рис. 2.3).

Под действием показанных на рисунке сил эта часть стержня находится в равновесии, т. е. для нее должны выполняться шесть уравнений равновесия:

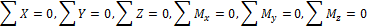
Рис. 2.3. Схема распределения внутренних усилий

в поперечном сечении стержня

Из шести неизвестных усилий только одно проектируется на какую-либо ось или дает момент относительно нее. Поэтому из условий равновесия легко получим:

Из данных формул следует, что:

1) продольная сила N равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на ось стержня. N > 0, если проекция внешней силы направлена от сечения;

2) поперечные силы Q_y и Q_хравны алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на оси у и х соответственно. Q_у > 0 и Q_х > 0, если при взгляде с положительного направления осей х и у соответственно проекция внешней силы вращает стержень относительно сечения по часовой стрелке;

3) изгибающие моменты 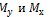равны алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения, относительно осей y и х соответственно. 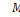> 0 и если внешняя сила или момент так изгибают стержень, что вогнутость его располагается со стороны положительных осей х и y соответственно.

4) крутящий момент М_кр равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения, относительно оси стержня. М_кр > 0, если при взгляде со стороны внешней нормали к сечению стержня внешняя сила или момент совершают вращение по часовой стрелке. Например, в рассматриваемом случае, от действия силы и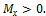

Таким образом, в общем случае действия внешних сил на стержень в его сечениях возникают четыре вида усилий: продольная сила (N), поперечные силы (Q_y, Q_x), крутящий момент (М_кр) и изгибающие моменты (М_у, М_х).

Каждый вид усилий вызывает характерную для него деформацию. Напряженно-деформированное состояние бруса, вызванное действием:

1) продольной силы (N), называется растяжением или сжатием;

2)поперечной силы (Q) – сдвигом;

3) крутящим моментом (М_кр) – кручением;

4) изгибающим моментом (М_у или М_х) – изгибом.

Все эти виды деформаций называются простыми.

Деформация, вызванная совместным действием двух и более усилий, называется сложной. В таких случаях говорят, что стержень испытывает сложное сопротивление. В расчетной практике наиболее часто встречаются следующие случаи сложного сопротивления.

Поперечный изгиб – деформация, вызванная совместным действием изгибающего момента и поперечной силы.

Пространственный или косой изгиб – деформация, вызванная совместным действием двух изгибающих моментов.

Изгиб с растяжением (сжатием) – деформация, вызванная совместным действием изгибающих моментов и продольной силы.

Изгиб с кручением – деформация, вызванная совместным действием изгибающих и крутящего моментов.

2.4. Контрольные вопросы

1. В чем заключается метод сечений?

2. Как определяются внутренние усилия в поперечных сечениях стержня?

3. Что такое полное напряжение в поперечных сечениях стержня, как оно определяется?

4. Нормальные и касательные напряжения, их определение.