Выпуклые (вогнутые) функции одной переменной. Точка перегиба.

Вторая производная. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x₀ ), то её производная называется второй производнойфункции f ( x ) в точке ( x₀ ), и обозначаетсяf '' ( x₀ ).

Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f( x ) в любой точке ( x₀, f ( x₀ ) ), x₀ 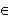(a, b ).

Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f( x ) в любой точке ( x₀, f ( x₀ ) ), x₀ 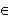(a, b ).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x 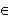( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x 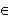( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, чтоесли в точке перегиба x₀ существует вторая производная f '' ( x₀ ), то f '' ( x₀ ) = 0.

П р и м е р .

Рассмотрим график функции y = x3 : 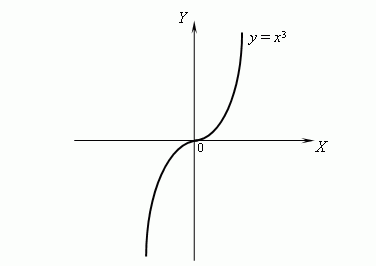Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x > 0 при x > 0 и 6x < 0при x < 0,следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3 является вогнутой при x > 0 и выпуклой при x <0. Тогда x = 0 является точкой перегиба функции y = x3.

Вертикальные и невертикальные асимптоты графика функции одной переменной.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).

Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.

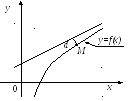Рис. 5.10

Вертикальные асимптоты

Определение. Прямая 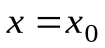называетсявертикальной асимптотой графика функции 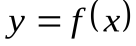, если выполнено одно из условий:

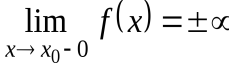или 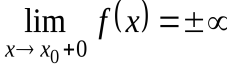(рис.5.11)

Рис. 5.11

Вертикальные асимптоты, уравнение которых х=x₀ , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны 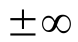. Если таких точек нет, то нет и вертикальных асимптот Например, для кривой 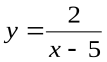, вертикальной асимптотой будет прямая 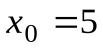, так как 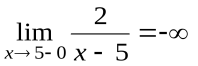, 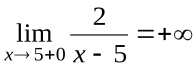. Вертикальной асимптотой графика функции 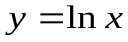является прямая 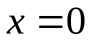(осьОу), поскольку .

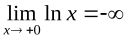Горизонтальные асимптоты Определение. Если при 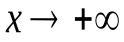( 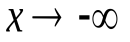) функция 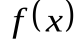имеет конечный предел, равный числуb: 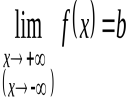, то прямая 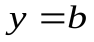есть горизонтальная асимптота графика функции 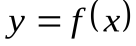. Например, для функции 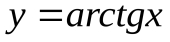имеем 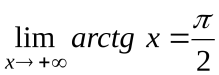, 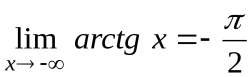.Соответственно, прямая 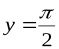− горизонтальная асимптота для правой ветви графика функции 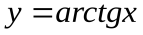, а прямая 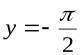− для левой ветви. В том случае, если 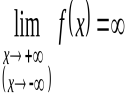, график функции не имеет горизонтальных асимптот, но может иметь наклонные.

Наклонные асимптоты Определение. Прямая 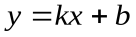называетсянаклонной асимптотой графика функци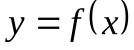и при 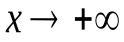( 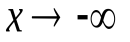), если выполняется равенство .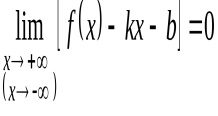