Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.

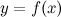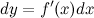32. Производные и дифференциалы высших порядков функции одной переменной и их свойства. Пусть функция зависит от переменной и дифференцируема в точке . Может оказаться, что в точке дифференциал , рассматриваемый как функция от , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 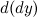данной функции, который называется дифференциалом второго порядкафункции 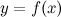. Дифференциал второго порядка обозначается следующим образом: 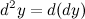Аналогично определяются дифференциалы более высоких порядков. Дифференциалом 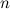-го порядка 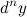функции 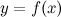называется дифференциал от дифференциала 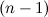-го порядка этой функции, то есть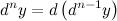

Случай независимой переменной Пусть 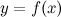- функция независимой переменной , имеющая дифференциалы любого порядка. Первый дифференциал функции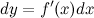

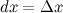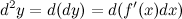где - некоторое приращение независимой переменной , которое мы задаем сами и которое не зависит от . По определению Переменной является аргумент . Значит, для дифференциала величина 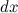является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка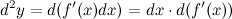

Для вычисления дифференциала 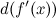применим формулу дифференциала первого порядка к функции 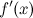. Тогда получим: 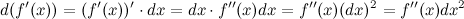Итак, 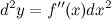Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала 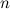-го порядка: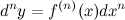

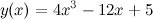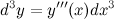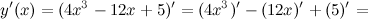
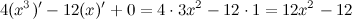
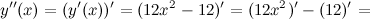
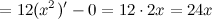
Задание. Найти дифференциал третьего порядка функции Решение. По формуле Найдем третью производную заданной функции: 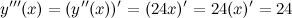Тогда 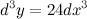Ответ.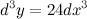

d2 f

dx2

Пусть в интервале (a, b) задана функция f(x) и в каждой точке x Î (a, b) существует производная f '(x). Таким образом в интервале (a, b) задана функция y =f '(x) .Если первая производная функция y = f '(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f(x).

Вторая производная обозначается символами f ''(x) или

Вообще, производной n–го порядка функции f(x), называется производная от производной функции f(x) (n − 1)–го порядка. Производная n–го порядка обозначается f⁽ⁿ⁾ (x). Замечание. Если речь идет о производной n–го порядка ( n = 2, 3, … ) в фиксированной точке x₀, то для существования f⁽ⁿ⁾ (x₀) необходимо существованиеf^{(n − 1)} (x) не только в точке x₀, но и в некоторой ее окрестности. При этом условии f⁽ⁿ⁾ (x₀)=d dx f^{(n − 1)} (x₀).

Функция, имеющая в точке производную n–го порядка, называется n раз дифференцируемой в этой точке. Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.

Формулы для производных n–го порядка суммы и произведения функций

Если функции u(x) и v(x) n раз дифференцируемы на некотором промежутке, то производная n–го порядка суммы определяется формулой

( u + v )(n) = u(n) + v(n) ,

а производная n–го порядка произведения определяется формулой Лейбница

( u · v)(n) = u(n) · v + n u(n − 1) · v' + n(n − 1) 2! u(n − 2) · v'' + … + u · v(n) .

Формула Лейбница может быть записана в виде

(u · v)(n) = n ∑ k = 0 Cnk · u(n − k) v(k) ,

n!

k! (n − k)!

где u⁽⁰⁾ = u(x), v⁽⁰⁾ = v(x) и C_n^k = — биномиальные коэффициенты.

33. Теорема Ролля, Лагранжа и Коши.

Теорема Ролля Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0. Доказательство. Так как функция f(x) непрерывна на [a, b],то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m. Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана. Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.

Геометрический смысл теоремы Ролля Геометрическитеорема Ролля означает, что у графика непрерывной на отрезке [a, b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах f(a) = f(b) равные значения, существует точка (c; f(c)), в которой касательная параллельна оси Оx.

Теорема Лагранжа Если функция f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то существует такая точка с Î (a, b), что выполняется равенство f(b) − f(a) = f '(c)·(b − a).

Д о к а з а т е л ь с т в о. Составим уравнение хорды, проходящей через точки (a, f(a)), (b, f(b))

y = f(a) + Q·(x - a), где 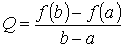есть угловой коэффициент хорды. Рассмотрим разность ординат функции и хорды F(x) = f(x) − f(a) − Q·(x − a). Очевидно, что функция F(x) удовлетворяет всем условиям теоремы Ролля. Поэтому на интервале (a, b) найдётся такая точка с, для которой F ' (c) = 0. То есть F ' (c) = f ' (c) − Q = 0. Откуда следует 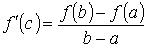. И, наконец, f(b) − f(a) = f '(c)·(b − a).

Геометрический смысл теоремы Лагранжа Величина 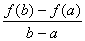является угловым коэффициентом секущей, проходящей через точки M₁ (a; f(a)) и M₂(b; f (b)) графика функции у = f(x), a f ' (c) — угловой коэффициент касательной к графику в точке (c; f (c)). Из теоремы Лагранжа следует, что существует точка "c" такая, что касательная к графику в точке (c; f(c)) параллельна секущей M₁M₂. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует. Замечание. Формула Лагранжа по структуре похожа на формулу линеаризации f (x) − f (x₀) ≈ f '(x₀)·(x −x₀).

Отличие только лишь в выборе точки для подсчета значения производной и в знаке равенства.

Теорема Коши Пусть функции f (x) и g(x) непрерывны на [a, b] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c Î (a, b), такая, что справедлива формула

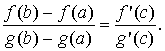Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g(b) = g(a), то по теореме Ролля для функции g(x) найдется точка x Î (a, b), в которой g ' (x) = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b). Рассмотрим функцию

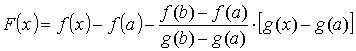.Функция F(x) на [a, b] удовлетворяет условиям теоремы Ролля: F(x) непрерывна на [a, b], дифференцируема на (a, b), и, кроме того, на концах интервала принимает равные значения F(a) = F(b) = 0. По теореме Ролля для F(x) существует точка c Î (a, b) , такая ,что F ' (c) = 0. Так как 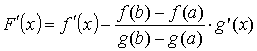, то 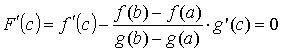. Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.

Правило Лопиталя.

Первое правило Лопиталя

Пусть функции f (x) и g (x) непрерывны на отрезке [а, b] и дифференцируемы на интервале (а, b), и пусть g ' (x) ≠ 0 всюду в (а, b). Пусть, далее, известно, что f (а) = g (а) = 0. Тогда говорят, что отношение 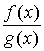при х → а + 0 представляет собой неопределённость вида 0/0.Теорема. Если при указанных условиях

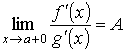, то и 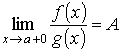. Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х₀ так, чтобы в интервале (а, x₀) выполнялось неравенство .

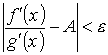Применим теорему Коши к отрезку [а, x₀], Если х [а, x₀], то существует такая точка с [а, x], что

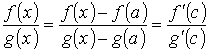и, следовательно, для всех х [а, x₀] справедливо неравенство

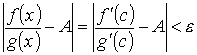. Это означает, что 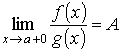. Второе правило Лопиталя Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g' (x) не обращается в нуль в (a, b). Пусть известно, что 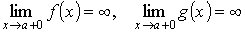. Тогда говорят, что отношение 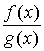прих → а + 0 представляет собой неопределённость вида . Теорема. Если при указанных условиях

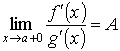, то и 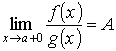. Доказательство. Пусть А конечно. Для заданного как угодно малого числа ε > 0 выберем х₀ так, чтобы в интервале (а, x₀) выполнялось неравенство

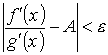. Определим функцию D(x, x₀) из условия 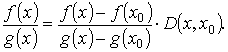. Имеем

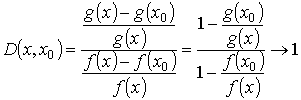при x → a + 0. Применяя к отрезку [x, x₀] теорему Коши, получаем, что некоторой точки с [x, x₀]

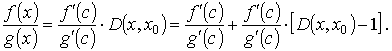Отсюда для всех х, для которых | D( x, x₀) - 1 | < ε, находим

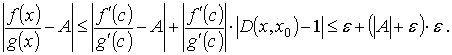Так как ε произвольно мало, то 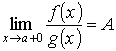, что и требовалось доказать.