Вопрос 20. Свойства неопределенного интеграла.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению

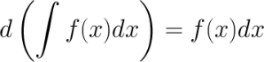
Пример

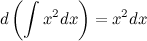
2. Производная от неопределенного интеграла равна подынтегральной функции

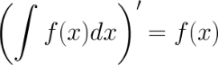
Пример

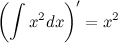
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

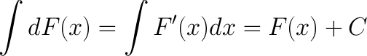
Пример

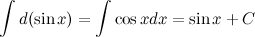
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

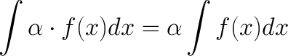
Пример

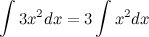
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

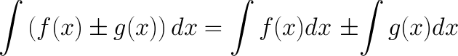
Пример

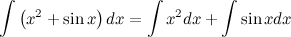
6. Если 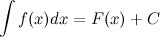, то и 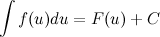, где функция 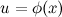- произвольная функция с непрерывной производной.

Пример

Известно, что 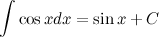, а тогда

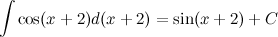
Вопрос 21. Интегралы от основных элементарных функций

Основные формулы

Вопрос 22. Метод замены переменной

Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся.

Если в неопределенном интеграле 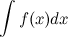сделать подстановку 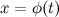, где функция 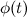- функция с непрерывной первой производной, то тогда 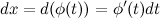и согласно свойству 6 неопределенного интеграла имеем, что:

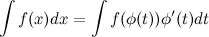
Эта формула называется формулой замены переменной в неопределенном интеграле.

Замечание

После нахождения интеграла по новой переменной 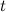необходимо вернуться к первоначальной переменной .

Замечание

В некоторых случаях целесообразно делать подстановку 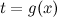, тогда

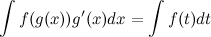
Пример

Задание. Найти интеграл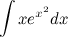

Решение. Сделаем замену переменной: 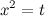, далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.

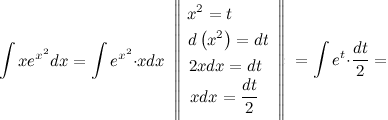
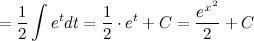
Ответ.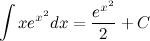

Вопрос 23. Метод интегрирования по частям

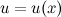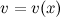Рассмотрим функции и , которые имеют непрерывныепроизводные. Согласно свойствам дифференциалов, имеет место следующее равенство:

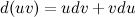
Проинтегрировав левую и правую части последнего равенства, получим:

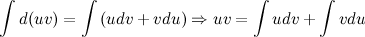
Полученное равенство перепишем в виде:

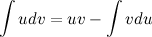
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл 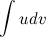можно свести к нахождению интеграла 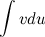, который может быть более простым.

Замечание

В некоторых случаях формулу интегрирования частями нужно применять неоднократно.

Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:

1) ; ;

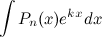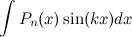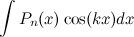
Здесь 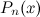- многочлен степени 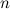, 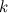- некоторая константа. В данном случае в качестве функции берется многочлен, а в качестве 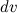- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 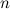раз.

Примеры решения интегралов данным методом

Пример

Задание. Найти интеграл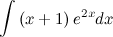

Решение. В исходном интеграле выделим функции и , затем выполним интегрирование по частям.

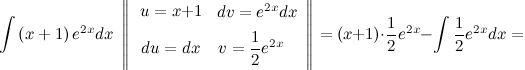
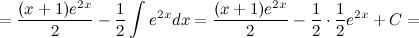
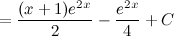
Ответ.