Вопрос 18. Общая схема исследования функции.
При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру:
1. Область определения 
и область допустимых значений 
функции.
2. Четность, нечетность функции.
3. Точки пересечения с осями.
4. Асимптоты функции.
5. Экстремумы и интервалы монотонности.
6. Точки перегиба и промежутки выпуклости, вогнутости.
7. Сводная таблица.
Замечание
Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика.
Замечание
Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание
Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Задание. Исследовать функцию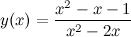 
и построить ее график.
Решение. 1) Область определения функции.
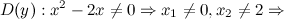
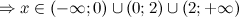
2) Четность, нечетность.
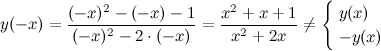
Функция общего вида.
3) Точки пересечения с осями.
а) с осью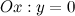 
:
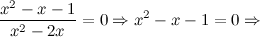
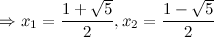
то есть точки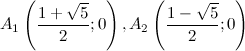 
б) с осью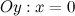 
: в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые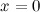 
и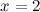 
- вертикальные асимптоты.
б) горизонтальные асимптоты:
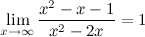
то есть прямая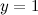 
- горизонтальная асимптота.
в) наклонные асимптоты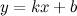 
:
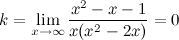
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
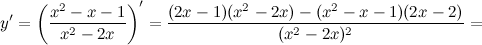
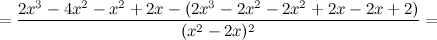
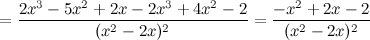
Найдем точки, в которых первая производная равна нулю или не существует: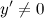 
для любого 
из области определения функции;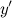 
не существует пр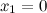и 
и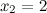 
.
Таким образом, функция убывает на всей области существования.Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.
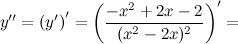
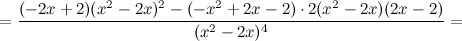
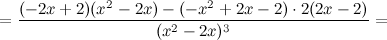
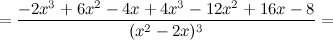
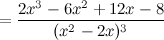
Найдем точки, в которых вторая производная равна нулю или не существует: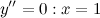 
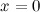; при и 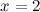вторая производная не существует.
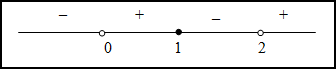
Таким образом, на промежутках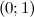 
и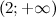 
функция вогнута, а на промежутках 
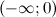и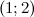 
- выпукла. Так как при переходе через точку 
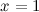вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
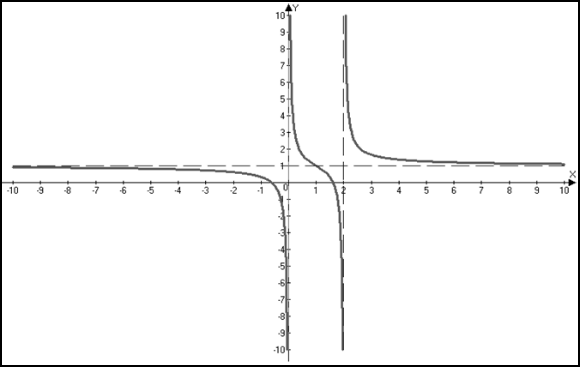
Вопрос 19. Первообразная функция и неопределенный интеграл
Функция 
называется первообразной для функции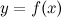 
на промежутке 
, конечном или бесконечном, если функция дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
Последнее равенство можно записать через дифференциалы:
или 
Пример
Функция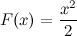 
является первообразной для функции 
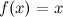, так как
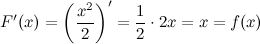
Совокупность всех первообразных функции 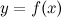, определенных на заданном промежутке, называется неопределенным интегралом от функции 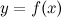и обозначается символом 
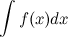. То есть
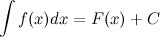
Знак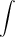 
называется интегралом, 
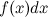- подынтегральным выражением, 
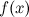- подынтегральной функцией, а - переменной интегрирования.