Раскройте суть функции распределения случайной величины.

Определение

Функция распределения случайной величины 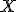- это числовая функция, которая имеет вид:

, .

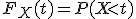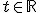Обозначение 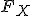используется для того, чтобы подчеркнуть, о какой случайной величине идет речь; если это ясно из контекста, то часто индекс опускают и обозначают функцию распределения просто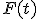

Свойства

Функция распределения 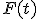определена на всей числовой оси и обладает следующими свойствами, вытекающими из свойств вероятностной меры:

1.

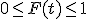
2. , .

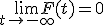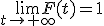3. Функция распределения является неубывающей: если 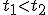, то

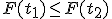
4. Функция распределения непрерывна слева: 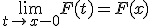для любого .

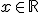Примечание. Последнее свойство обозначает, какие значения принимает функция распределения в точках разрыва. Иногда определение функции распределения формулируют с использованием нестрогого неравенства: 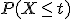. В этом случае непрерывность слева заменяется на непрерывность справа: 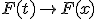при 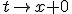. Никакие содержательные свойства функции распределения при этом не меняются, поэтому данный вопрос является лишь терминологическим.

Свойства 1-4 являются характеристическими, т.е. любая функция 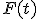, удовлетворяющая этим свойствам, является функцией распределения некоторой случайной величины.

Функция распределения задает распределение вероятностей случайной величины однозначно. Фактически, она является универсальным и наиболее наглядным способом описания этого распределения.

Чем сильнее функция распределения растет на заданном интервале числовой оси, тем выше вероятность попадания случайной величины в этот интервал. Если вероятность попадания в интервал равна нулю, то функция распределения на нем постоянна.

В частности, вероятность того, что случайная величина 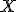примет заданное значение 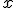, равна скачку функции распределения в данной точке:

.

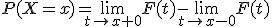Если функция распределения непрерывна в точке 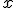, то вероятность принять данное значение для случайной величины равна нулю. В частности, если функция распределения непрерывна на всей числовой оси (при этом и соответствующее распределение называется непрерывным), то вероятность принять любое заданное значение равна нулю.

Из определения функции распределения вытекает, что вероятность попадания случайной величины в интервал, замкнутый слева и открытый справа, равна:

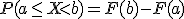
С помощью данной формулы и указанного выше способа нахождения вероятности попадания в любую заданную точку, легко определяются вероятности попадания случайной величины в интервалы других типов: 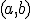, 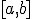и 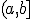. Далее, по теореме о продолжении меры, можно однозначно продолжить меру на все борелевские множества числовой прямой 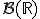. Для того, чтобы применить эту теорему, требуется показать, что таким образом определенная на интервалах мера является на них сигма-аддитивной; при доказательстве этого в точности используются свойства 1-4 (в частности, свойство непрерывности слева 4, поэтому отбросить его нельзя).