Прогнозирование определяющих параметров

Задача прогнозирования технического состояния одномерного объекта формулируется следующим образом.

Пусть контролируемый параметр X объекта в моменты контроля t₀, t₁, t₂, …t_n, принял значения x(t₀), x(t₁), …, x(t_n) по которым построен график x(t)(рис. 12.1).

t3

Необходимо по известным значениям х(t_i), i = 0, 1, 2,..., п в моменты t. в прошлом предсказать значения x(t_n+J) для моментов времени t_n+1, t_n+2, t_n+mв будущем. Здесь т - количество планируемых периодов между очередными проверками (например, число межрегламентных периодов).

Если период между очередными моментами контроля равен ∆T_кто прогнозируемый период равен Т_np =m∆T_к.

При монотонной функции x(t)(рис. 12.1) ее математическое представление удобно выразить в виде интерполяционной формулы Лагранжа:

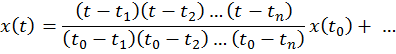
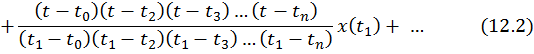
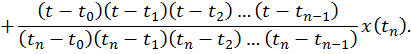
Легко можно проверить, что для любого из моментов 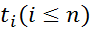справедливо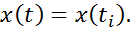

Поскольку 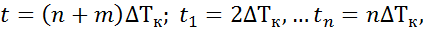где n - число реализованных межконтрольных периодов (общее число проверок при этом равно n + 1), 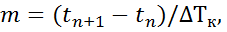то для прогнозируемого периода формула Лагранжа (12.2) преобразуется к следующему виду полинома порядка п:

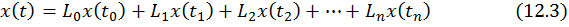
Коэффициенты Лагранжа определяются как

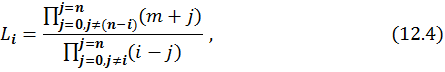
где m – число прогнозируемых межконтрольных периодов, на которое делится период прогнозирования.

Пример 12.1. По данным статистики выполнено четыре измерения: х(0) = 100; x(ΔT_к) = 95; х(2ΔT_к) = 87; х(3ΔT_к) = 79. При этом число межконтрольных периодов измерения параметра п = 3.

Требуется дать прогноз на значение параметра к концу двух предстоящих прогнозируемых межконтрольных периодов, т.е. т = 2.

Решение. Из (12.4) имеем:

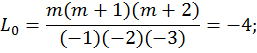
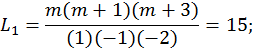
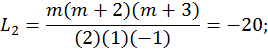
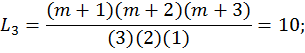
Прогнозируемое значение параметра x(t_n+2)находится подстановкой значений L_i и x(t_i) в (12.3):

x(t_n+2) = x(t₅) = – 4·100 + 15·95 – 20·87 + 10·79 = 75.

Пример 12.1а. Проведено 5 измерений через интервалы времени ΔT_k: x₀=56; x₁=59; x₂=62; x₃=69; x₄=74; Определить значение параметра для m = 3. Число межконтрольных периодов n = 4.

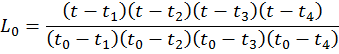
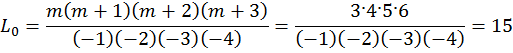
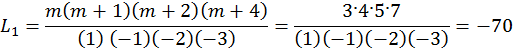
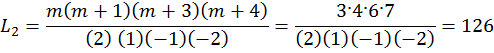
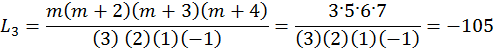
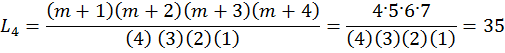
x(t_n+3) = x(t₇) = 15·56 – 70·59 + 126·62 –105·69 + 35·74 = 133.

Ошибка прогнозирования с использованием (12.3) не превышает 10... 15%, если число т = 1...3, а число предыдущих точек контроля п > 5. Для прогнозирования может использоваться также целый ряд других математических выражений, например, интерполяционная формула Ньютона и др.

На практике обычно характер изменения контролируемого параметра x(t)является сложным, близким к случайному. Поэтому не всегда удается найти аналитическое выражение для базовых полиномов, моделирующих функцию x(t)и пригодных для целей прогнозирования. В данном случае прогнозирование целесообразно рассматривать как вероятностную задачу с учетом изменений во времени распределения параметра.

Тема 6 (4 ч). СПОСОБЫ И СРЕДСТВА ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ ДИАГНОСТИРОВАНИЯ АВИАЦИОННОГО ОБОРУДОВАНИЯ

13.1. ЛОГИЧЕСКИЕ АНАЛИЗАТОРЫ РЕЗУЛЬТАТОВ

ДИАГНОСТИРОВАНИЯ

В процессе диагностирования бинарные значения проверок состояний, полученные с целью определения состояния объекта, могут обрабатываться как с помощью аналоговых анализаторов параметров, так и цифровыми вычислительными машинами (ЦВМ). Эти бинарные значения проверок записываются в ОЗУ, где идет их накопление. В ДЗУ хранится минимизированная таблица состояний объекта (например, табл. 11.12).

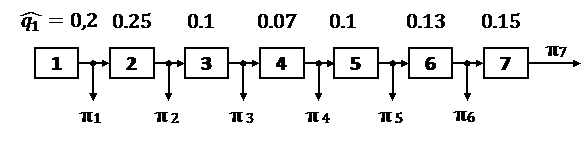
Рис. 11.2. Метод проверки половинным разбиением цепочки элементов

на части с равными вероятностями отказов

Таблица 11.12

Результат минимизации

SJ	S0	S1	S2	S3	S4	S5	S6	S7
PJ	0,8	0,05	0,05	0,02	0,02	0,02	0,02	0,02
π4
π2
π6
π3

В случае безусловного алгоритма диагностирования после окончания процесса последней проверки и записи ее результата в ОЗУ весь набор полученных проверок (тест Т) подается в компьютер. Здесь производится поочередное сравнение с этим набором каждого из столбцов таблицы состояний. В момент совпадения какого-то столбца с реализацией проверок выдается результат о состоянии объекта диагностирования.

Таблица состояний с полученным минимизированным набором проверок может использоваться для построения схемы логического анализатора состояний, построенного на логических ячейках И и НЕ, который может быть реализован и в цифровой аппаратуре диагностирования.

С целью упрощения схемы и конструкции анализатора полученную табл. 11.12 можно упростить. Полученный тест обеспечивает распознавание всех состояний друг от друга. Однако не все проверки теста необходимы для различения того или иного конкретного состояния от остальных. Определение минимального набора проверок для каждого конкретного состояния позволяет уменьшить число входов ячеек И и (иногда) уменьшить число ячеек НЕ. В результате обеспечивается минимизация схемы логического анализатора.

Определение минимальных наборов проверок из общего теста, необходимых для каждого конкретного состояния S_k, выполняется составлением частных различающих функций из минимизированной таблицы состояний. Например, из табл. 11.12 записываем и упрощаем различающую функцию только состояния S₀, определяющую условие его выделения из остальных. (+, или V) – логическая сумма, (·) – логическое произведение:

F₀ = (S₄+ S₂+S₃)·( S₄+S₂+S₆+S₃)·( S₄+S₂+S₃)·(S₄)·(S₄+S₃)·( S₂+ S₆)·( S₆) = S₄S₆.

Символ S₂ обозначим цифрой 2, символ S₃ – цифрой 3 и т.д. При этом F₀можно представить в виде

F₀ = (4V2V3)·(4V2V6V3)·(4V2V3)·(4)·(4V3)·(2V6)·(6) = 4·6.

В результате выполнения операций поглощения и логического перемножения определено, что проверки π₄ и π₆ достаточны для отличия состояния S₀от остальных.

Различающая функция только для состояния S₁:

F₁=(4V2V3)·(6)(2V6)·(2V3)·(2V6V3)·(4V6V3)·(4V2V6V3) = 6·3V6·2

Любая из этих конъюнкций может быть выбрана для различения состояния S от остальных.

Аналогично определяются частные различающие функции для остальных состояний:

F₁= 6·3V6·2; F₂ = 6·2·4V6·2·3; F₃ = 2·3;

F₄=4·2·6V4·3·6; F₅= 3 ·6·4; F₆=2·4; F₇= 6·4·2.

Результаты расчетов сводятся в табл. 13.1. По этой таблице строится схема логического анализатора результатов диагностирования, приведенная на рис. 13.1.

Таблица 11.12