Исследование функции на экстремум

Функция 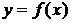называется возрастающей (убывающей)в некотором интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, то есть при 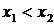выполняется неравенство < >

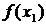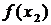
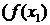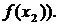
Для исследования функций применяются следующие признаки:

1. Если дифференцируемая функция 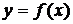на отрезке 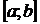возрастает (убывает), то ее производная на этом отрезке неотрицательна (неположительна), то есть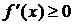

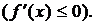
2. Если непрерывная на отрезке 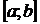и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.

Функция 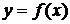называется неубывающей (невозрастающей) в некотором интервале, если для любых 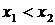из этого интервала .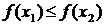

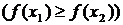Интервалы, в которых функция не убывает или не возрастает, называются интервалами монотонности функции. Характер монотонности функции может изменяться только в тех точках ее области определения, в которых меняется знак первой производной. Точки, в которых первая производная функции обращается в ноль или терпит разрыв, называются критическими или стационарными.

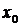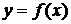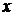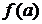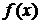
Точка называется точкой локального максимума (минимума) функции , если существует такая окрестность этой точки, что для всех точек из этой окрестности выполняется неравенство > 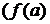< 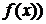. Точки максимума и минимума называются точками экстремума функции, а максимумы и минимумы функции – ее экстремальными значениями.

Для исследования функций на экстремум применяются следующие теоремы.

Теорема.Если функция 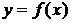имеет в точке 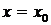экстремум, то либо 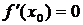, либо 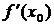не существует.

Для отыскания экстремумов функции находят все критические точки, а затем исследуют каждую из них по отдельности, чтобы выяснить будет ли в этой точке максимум или минимум, или же в ней нет экстремума.

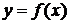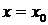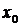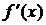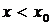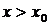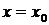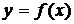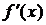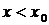Теорема. Пусть функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала (кроме, возможно, самой точки ). Если при положительна, а при отрицательна, то при функция , имеет максимум. Если же при отрицательна, а при 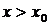положительна, то при 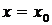данная функция имеет минимум.

На отрезке 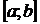функция 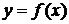может достигать наименьшего и наибольшего значения либо в критических точках функции, лежащих в интервале ( 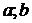), либо на концах отрезка .

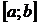Пример. Найти наименьшее и наибольшее значения функции

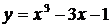на отрезке .

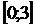Решение. Производная данной функции 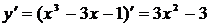. Тогда приравнивая производную функции к нулю, получаем уравнение 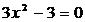, решая которое, находим критические точк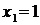и и .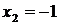

Точка 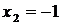не принадлежит исследуемому интервалу, поэтому ее исключаем из рассмотрения.

Вычисляем значение функции в критической точке 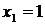и на концах отрезка:

,

,

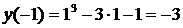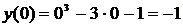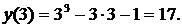
Сравнивая полученные числа, получаем, что наименьшее значение на отрезке 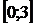функция принимает в точке 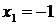, а наибольшее значение − в точке .

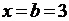Итак, на отрезке , .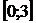

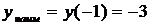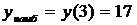Ответ: , .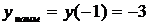

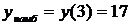Кривая, заданная функцией 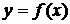, называется выпуклой в интервале 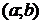, если все точки кривой лежат не выше любой ее касательной в этом интервале, и вогнутой в интервале 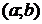, если все ее точки лежат не ниже любой ее касательной в этом интервале.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.

Для нахождения интервалов выпуклости и вогнутости графика функции и точек перегиба пременяются следующие теоремы.

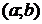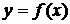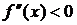
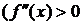
Теорема.Если во всех точках интервала вторая производная функции отрицательна (положительна), то есть 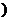, то кривая 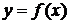в этом интервале выпукла ( вогнута).

Прямая 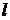называется асимптотой данной кривой 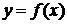, если расстояние от точки 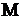кривой до прямой 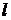при удалении точки 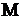в бесконечность стремится к нулю.

Если существуют числа 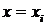( 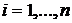), при которых 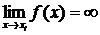, то есть функция имеет бесконечные разрывы, то прямые 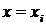называютсявертикальными асимптомами кривой .

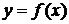Наклонная асимптома задается уравнением 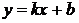, гдe, 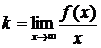, , 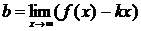если оба предела существуют и конечны. При 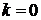получается частный случай наклонной асимптоты – горизонтальная.

Алгоритм полного исследования функции и построения графика:

1. Найти область определения функции.

2. Исследовать функцию на четность – нечетность.

3. Найти точки разрыва функции, и вертикальные асимптомы (если они существуют).

4. Найти точки пересечения графика функции с осями координат.

5. Найти наклонные асимптомы графика функции.

6. Найти экстремумы и интервалы монотонности функции.

7. Найти интервалы выпуклости и вогнутости, точки перегиба.

8. При необходимости выполнить дополнительные вычисления.

9. Построить график функции.

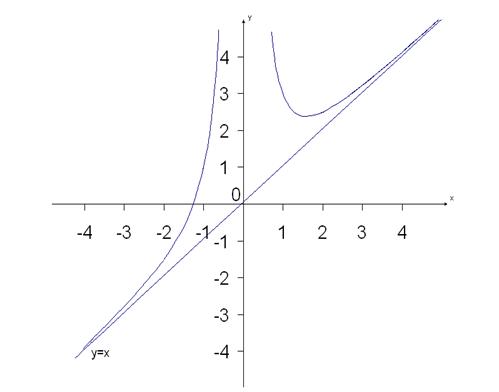
Пример. Провести полное исследование функции 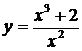и построить ее график.

Решение. 1. Функция не определена в тех точках, в которых знаменатель равен 0, то есть при 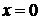. Область определения ; ; .

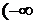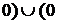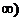2. Функция является четной, если 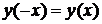и нечетной, если 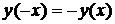, при условии, что область определения функции симметрична относительно начала координат.

.

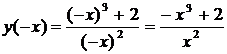Данная функция не является ни четной, ни нечетной.

3. Точка 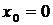является точкой разрыва функции. Так как левосторонний предел функции при 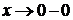и правосторонний предел функции при 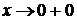бесконечны, то есть 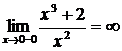и 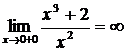, то прямая 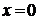(ось 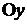) является вертикальной асимптотой.

4. Чтобы найти точки пересечения с осью 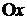приравниваем функцию к нулю и решаем полученное уравнение:

.

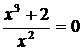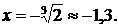
График функции пересекает ось 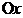в точке 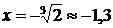. Для нахождения точки пересечения графика функции с осью 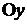необходимо вычислить значение функции при 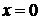. Так как исследуемая функция не определена при 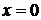, то нет точек пересечения с осью .

5. График функции имеет наклонную асимптому 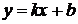, если существуют пределы для 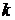и 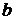. Вычислим их для данной функции:

,

.

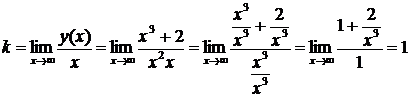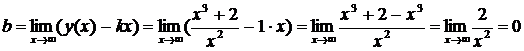Следовательно, уравнение наклонной асимптоты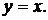

6. Находим производную функции:

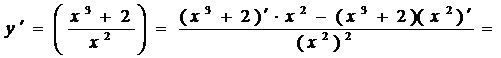
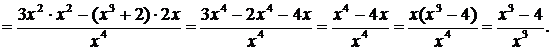
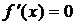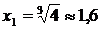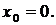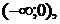
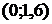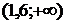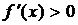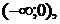
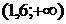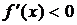при и не существует в точке Эти точки разбивают всю область определения функции на интервалы , . Внутри каждого из полученных интервалов производная сохраняет знак, а именно: на интервалах и на интервале 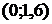. Это означает, что функция возрастает на интервале 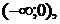убывает на интервале 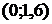и возрастает на интервале 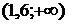. В точке 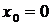функция не определена, она не является точкой экстремума, а точка 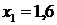является точкой минимума функции.

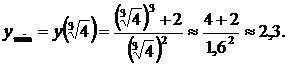
7. Находим вторую производную:

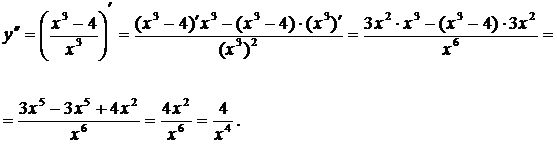
Вторая производная не равна 0 ни при каких значениях 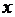, поэтому график функции не имеет точек перегиба. Точка 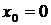, в которой не определена исследуемая функция, разбивает ее область определения на интервалы 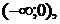и 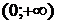. 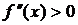на обоих интервалах, поэтому кривая вогнута на всей области определения.

8. Для более точного построения графика функции вычислим ее значения в нескольких точках:

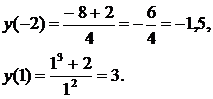
9. По результатам исследования строим график функции.