Решение типовых задач по линейной алгебре

Пример 1. Найти минор M22, алгебраическое дополнение A31

и вычислить определитель матрицы

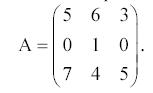
Решение: Вводим матрицу A. Для этого используем меню

Алгебра/Ввести матрицу … В первой форме вводим число строк

и число столбцов равно 3, а во второй форме вводим элементы

матрицы A. Переход к очередному элементу осуществляем при

помощи клавиши Tab. После ввода матрицы строку с вызовом

функции matrix можно откорректировать. Для этого дважды

щелкнуть на формуле и впереди добавить : A и расположить

формулу на одной строке. После этого пересчитать исправления,

подав команду Ctrl+R. Получаем:

Получили правую часть. Следовательно, система линейных

алгебраических уравнений решена правильно.

б) Решаем систему методом Крамера. На базе матрицы A

получаем три вспомогательные матрицы: A1, A2 и A3. В матрице

A1, вместо первого столбца, в матрице A2, вместо второго столб-

ца и в матрице A3, вместо третьего столбца, подставляем вектор

A1:addcol(b,submatrix(A,1));

A2:addcol(col(A,1),b,col(A,3));

A3:addcol(submatrix(A,3),b);

Вычисляем определитель матрицы A

d:determinant(A);

Применяем формулы Крамера.

x:matrix([determinant(A1)], [determinant(A2)], [determinant(A3)])/d;

Получили ответ: matrix([2],[-5],[3]).

Задачи математического анализа

При решении задач математического анализа с помощью пакета

Maxima используется пункт меню Анализ.

.

Вычисление пределов числовых последователь-

Ностей и функций

Решим теперь некоторые примеры из нулевого варианта за-

дания по пределам из сборника типовых расчетов

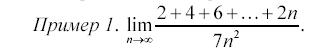
Решение. В числители находится сумма n слагаемых. Сна-

чала вычислим эту сумму. Для этого нажимаем на кнопку Ряды… и заполняем форму

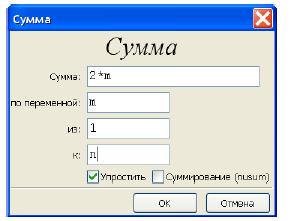
Maxima формирует и выполняет команду

sum(2*m, m, 1, n), simpsum;

Результатом выполнения данной команду будет выражение .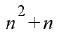

Используем его при вычислении предела. Вызываем ко-

манду Предел … и заполняем форму следующим образом:

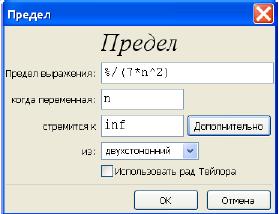
Символ % означает выражение, полученное предыдущей командой. Inf обозначается символ бесконечности и для его ввода можно использовать кнопку Дополнительно.В результате получаем ответ: 1/7

Пример 2.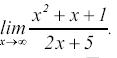

Вызываем команду Предел … и заполняем предложенную форму

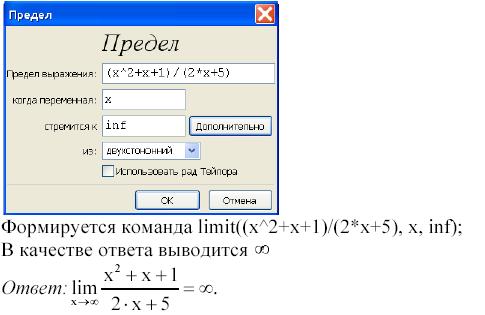
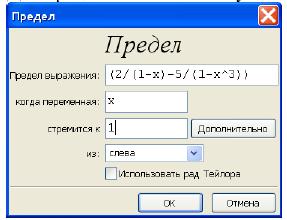
Однако, генерируется та же команда. Как и большинстве

программ в wxMaxima есть ошибки, которые в последующих

версиях исправятся.

Выделяем строку с командой limit и нажимаем клавишу F1.

Попадаем в справочник по данной команде.

limit(expr, x, val, dir)

limit(expr, x, val)

limit(expr, x)

В данном случае нам подходит первая команда. Необяза-

тельный параметр dir указывает направление вычисления преде-

ла. Он принимает два значений: plus и minus.

Команда limit((2/(1-x)-5/(1-x^3)), x, 1,plus) дает результат

Команда limit((2/(1-x)-5/(1-x^3)), x, 1,minus) дает результат

Ответ: Предел слева равен . , а справа – .. .

Пример 5.

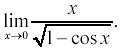
Решение. Находим предел данной функции, вводя команду

limit(x/sqrt(1-cos(x)),x,0). Однако, получаем ту же формулу.

Т.е., Maxima с задачей не справилась. Команды limit(x/sqrt(1-

cos(x)),x,0,minus) и limit(x/sqrt(1-cos(x)),x,0,plus) для пределов

слева и справа дают тот же результат. Если упростить выражение

в знаменателе используя формулу

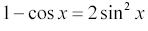
Получим